LeetCode 1954. 收集足够苹果的最小花园周长：数学O(1)的做法

【LetMeFly】1954.收集足够苹果的最小花园周长：数学O(1)的做法

力扣题目链接：https://leetcode.cn/problems/minimum-garden-perimeter-to-collect-enough-apples/

给你一个用无限二维网格表示的花园，每一个?整数坐标处都有一棵苹果树。整数坐标?(i, j)?处的苹果树有 |i| + |j|?个苹果。

你将会买下正中心坐标是 (0, 0)?的一块 正方形土地?，且每条边都与两条坐标轴之一平行。

给你一个整数?neededApples?，请你返回土地的?最小周长?，使得?至少?有?neededApples?个苹果在土地?里面或者边缘上。

|x|?的值定义为：

• 如果?x >= 0?，那么值为?x
• 如果?x <?0?，那么值为?-x

?

示例 1：

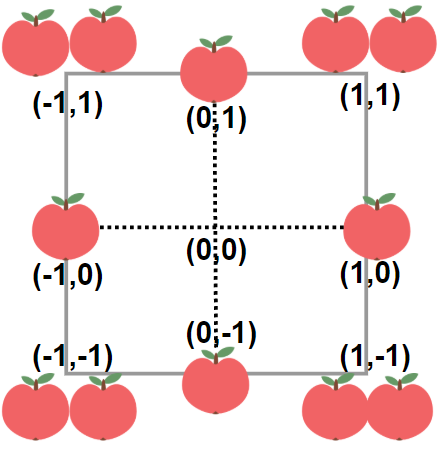
输入：neededApples = 1
输出：8
解释：边长长度为 1 的正方形不包含任何苹果。
但是边长为 2 的正方形包含 12 个苹果（如上图所示）。
周长为 2 * 4 = 8 。

示例 2：

输入：neededApples = 13
输出：16

示例 3：

输入：neededApples = 1000000000
输出：5040

?

提示：

• 1 <= neededApples <= 1015

方法一：求公式

边长为$2n$的正方形，苹果数量为多少呢？

由于X和Y是相互独立的，因此二者可以分开来看。对于X：

边长为$2n$的正方形一共有$2n+1$行，每行有Y轴左右共$2$部分。只考虑其中一行Y轴右侧的部分：

对苹果的总贡献数为$0+1+2+?+n=\frac{n(n+1)}{2}$

因此所有的X的贡献为$(2n+1)\times 2\times \frac{n(n+1)}{2}=n(n+1)(2n+1)$

由于Y与X类似，所以Y的贡献与X相同，因此边长为2n的正方形的苹果数为$2n(n+1)(2n+1)$

$n$为多少才能至少有neededApples个苹果呢？

将上式处理一下：$2n(n+1)(2n+1)=4n(n+1)(n+0.5)\approx 4n^3$并且大于$4n^3$

也就是说要求的$n$就在$\sqrt[3]{\frac{1}{4}neededApples}$附近。令$m=\sqrt[3]{\frac{1}{4}neededApples}$，其实从$?m??10$到$?m?+10$算一遍就直到答案了。

有没有更靠谱/可信一点的证明？ （此部分可跳过）

令$n=?m?$，令$f(n)=n(n+1)(n+0.5)$，则是在求最小的$n$使得$f(n)\ge \frac{1}{4}neededApples$。因为有：

1. $f(n?1)=(n?1)n(n?0.5)<n^3\le m^3=\frac{1}{4}neededApples$，因此$n?1$必定偏小
2. $f(n+1)=(n+1)(n+2)(n+1.5)>(n+1{)}^3=?m{?}^3>\frac{1}{4}neededApples$，因此$n+1$必定满足要求

所以答案$ans$的范围是：$[n,n+1]$，其中$n=?m?=?\sqrt[3]{\frac{1}{4}neededApples}?$。

因此只需要先计算出$?\sqrt[3]{\frac{1}{4}neededApples}?$，并在不满足要求（苹果数偏少）时不断加加一，直到满足要求即可。（最多会加1次一）

• 时间复杂度$O(1)$，开立方根有内置库，可视为$O(1)$时间复杂度
• 空间复杂度$O(1)$

AC代码

C++

/*
x: 2(2n+1)(1+2+...+n)=n(n+1)(2n+1)
y = x
x + y: 2n(n+1)(2n+1) = 4n(n+1)(n+0.5)≈4n^3
*/
class Solution {
public:
    long long minimumPerimeter(long long neededApples) {
        long long ans = cbrt((double)0.25 * neededApples);
        while (2 * ans * (ans + 1) * (2 * ans + 1) <  neededApples) {
            ans++;
        }
        return ans * 8;
    }
};

Python

# from numpy import cbrt

class Solution:
    def minimumPerimeter(self, neededApples: int) -> int:
        ans = int(cbrt(0.25 * neededApples))
        while 2 * ans * (ans + 1) * (2 * ans + 1) < neededApples:
            ans += 1
        return ans * 8

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/135183907