Bezier 曲线拼接圆
Bezier 曲线拼接
为了描述复杂物体的轮廓曲线,经常需要将多段 Bezier 曲线拼接起来,并在结合处满足一定的连续性条件。
假设两段 三次 Bezier 曲线分别为 p ( t ) p(t) p(t) 和 q ( t ) q(t) q(t),其控制多边形的顶点分别为 P 0 P_0 P0?, P 1 P_1 P1? , P 2 P_2 P2?, P 3 P_3 P3? 和 Q 0 Q_0 Q0?, Q 1 Q_1 Q1? , Q 2 Q_2 Q2?, Q 3 Q_3 Q3?
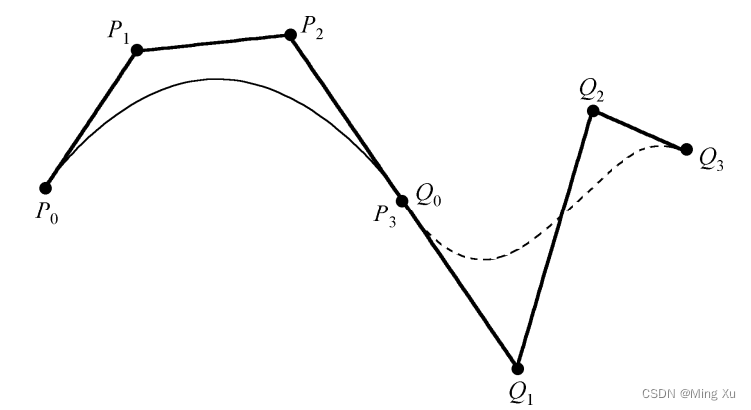
两段三次 Bezier 曲线 达到
G
0
G^0
G0 连续的条件是,
P
3
=
Q
0
P_3 = Q_0
P3?=Q0?, 在这一点处有相同的切线方向,
G
1
G^1
G1 连续的条件是,
P
2
P_2
P2?,
p
3
或
(
Q
1
)
p_3或 (Q_1)
p3?或(Q1?) 和
Q
2
Q_2
Q2? 三点共线。
Bezier 曲线拼接圆
使用一段三次 Bezier 曲线绘制拼接圆
参考 《孔令德 计算几何算法与实现》
#include <QWidget>
#include <QApplication>
#include <QPainter>
#include <QPointF>
#include <vector>
#include <QPainterPath>
#include <iostream>
const double m = 0.5523; // 魔术常数
std::vector<QPointF> getControlPoints(float radius) {
std::vector<QPointF> controlPoints = {
QPointF(radius, 0.0),
QPointF(radius, m * radius),
QPointF(m * radius, radius),
QPointF(0.0, radius),
QPointF(-m * radius, radius),
QPointF(-radius, m * radius),
QPointF(-radius, 0.0),
QPointF(-radius, -m * radius),
QPointF(-m * radius, -radius),
QPointF(0.0, -radius),
QPointF(m * radius, -radius),
QPointF(radius, -m * radius)
};
return controlPoints;
}
void drawControlPoints(QPainter* painter, const QPointF& center, const std::vector<QPointF>& controlPoints, const QColor& circleColor, int radius = 5)
{
// 设置空心圆圈的颜色
painter->setPen(circleColor);
painter->setBrush(Qt::NoBrush); // 空心圆圈
// 计算控制点的绝对坐标
for (int i=0; i<controlPoints.size(); i++)
{
QPointF point = center + controlPoints[i];
painter->drawEllipse(point, radius, radius);
}
}
void drawControlPolygon(QPainter* painter, const QPointF& center, const std::vector<QPointF>& controlPoints, const QColor& lineColor) {
// 设置线条颜色
QPen pen(lineColor);
painter->setPen(pen);
// 绘制控制点之间的直线
for (int i = 0; i < controlPoints.size(); ++i) {
QPointF startPoint = center + controlPoints[i];
QPointF endPoint = center + controlPoints[(i + 1) % controlPoints.size()];
painter->drawLine(startPoint, endPoint);
}
}
QPointF calculateCubicBezierPoint(float t, const QPointF& P0, const QPointF& P1, const QPointF& P2, const QPointF& P3)
{
float u = 1 - t;
float b0 = u * u * u;
float b1 = 3 * u * u * t;
float b2 = 3 * u * t * t;
float b3 = t * t * t;
return b0 * P0 + b1 * P1 + b2 * P2 + b3 * P3;
}
void CubicBezierCurve(QPainter* painter, const QPointF& P0, const QPointF& P1, const QPointF& P2, const QPointF& P3)
{
float tStep = 0.01f;
QPainterPath bezierPath;
QColor curveColor(255, 0, 0); // 红色
painter->setPen(curveColor);
bezierPath.moveTo(P0);
for (float t = tStep; t <= 1.0f; t += tStep)
{
QPointF P = calculateCubicBezierPoint(t, P0, P1, P2, P3);
bezierPath.lineTo(P);
}
painter->drawPath(bezierPath);
}
class MyWidget : public QWidget
{
public:
MyWidget(QWidget* parent = nullptr) : QWidget(parent) {
setFixedSize(1000, 800);
}
protected:
void paintEvent(QPaintEvent* event) override {
Q_UNUSED(event);
QPainter painter(this);
painter.setRenderHint(QPainter::Antialiasing, true);
float radius = 200.0;
QPointF center(500, 400); // 圆心坐标
std::vector<QPointF> controlPoints = getControlPoints(radius);
for (int i = 0; i < controlPoints.size(); i += 3) {
CubicBezierCurve(&painter, center + controlPoints[i], center + controlPoints[i + 1], center + controlPoints[i + 2], center + controlPoints[(i + 3) % controlPoints.size()]);
}
QColor lineColor(0, 0, 255);
// 调用绘制控制多边形的函数,并传入线条颜色
drawControlPolygon(&painter, center, controlPoints, lineColor);
QColor circleColor(0, 255, 0);
drawControlPoints(&painter, center, controlPoints, circleColor,6);
}
};
int main(int argc, char* argv[]) {
QApplication app(argc, argv);
MyWidget widget;
widget.show();
return app.exec();
}

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!