无监督学习-聚类算法(k-means)

无监督学习-聚类算法

1、聚类介绍

1.1、聚类作用

• 知识发现
• 异常值检测
• 特征提取 数据压缩的例子

---

1.2、有监督与无监督学习

有监督：

• 给定训练集X和标签Y
• 选择模型
  • 学习（目标函数的最优化）
  • 生成模型（本质上是一组参数、方程）

根据生成的一组参数进行预测分类任务

无监督：

• 拿到的数据只有X没有标签，只能根据X的相似程度做一些事情
• Clustering 聚类：
  • 对于大量未标注的数据集，按照内在的相似性来分为多个类别（簇）目标：类别内相似度大，类别内相似度大，类别间相似小
  • 也可以用来改变数据的维度，可以将聚类结果作为一个维度添加到训练数据中。
  • 降维算法，数据特征变少

1.3 聚类算法

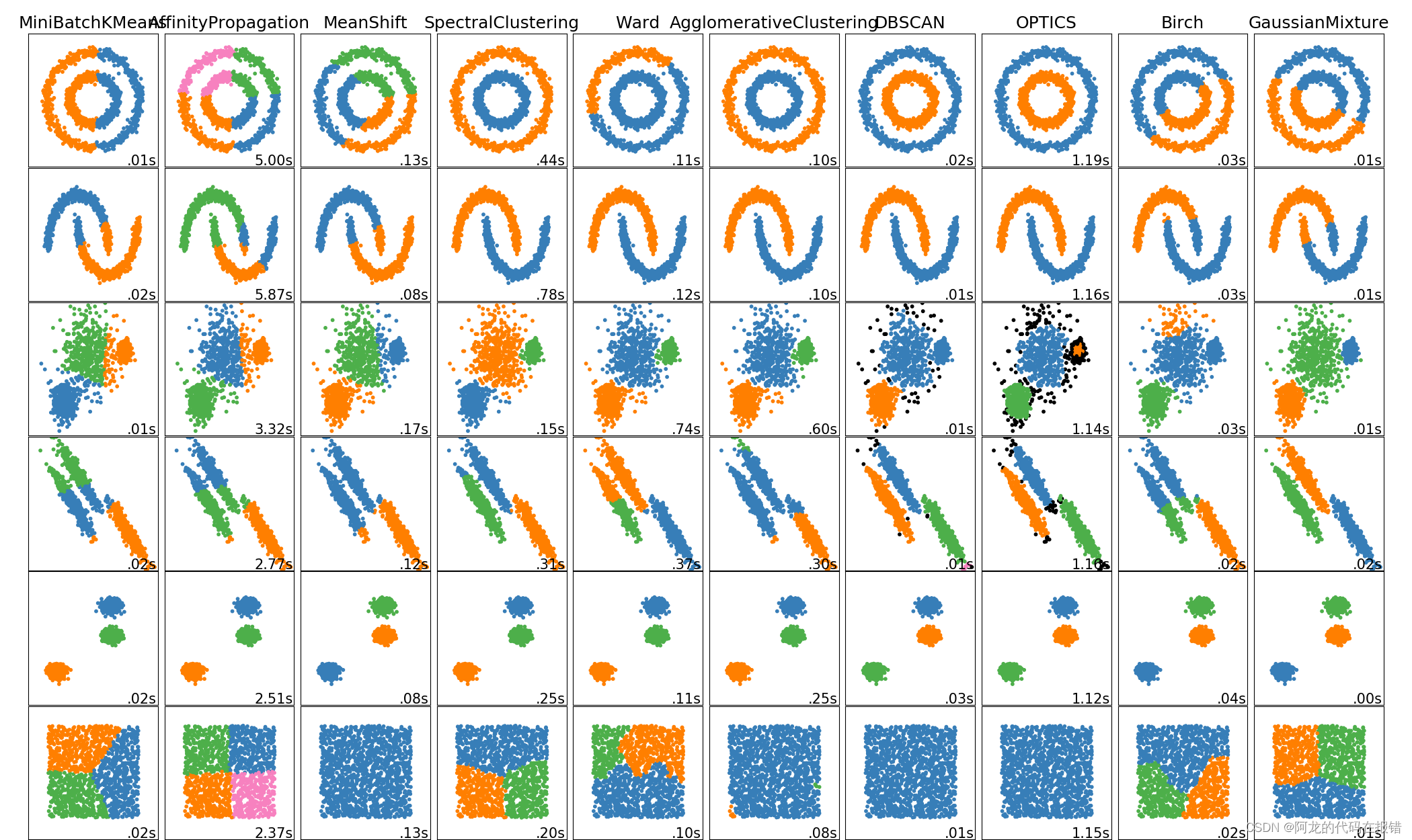
图片来源：https://scikit-learn.org.cn/view/108.html

---

1.4 数据间的相似度

• 每一条数据都可以理解为多维空间中的一个点。
• 可以根据点和点之间的距离来评价数据间的相似度

---

1.5 余弦距离

将数据看做空间的中的点的时候，评价远近可以用欧式距离或者是余弦距离
计算过程如下：

• 将数据映射为高维空间中的点（向量）
• 计算向量间的余弦值
• 取值范围[-1,+1]趋于近于1代表相似，越趋于-1代表方向相反，0代表正交
  $cos\theta =\frac{a?b}{||a|{|}_2||b|{|}_2}$

$cos\theta =\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}\times \sqrt{x_2^2+y_2^2}}$

• 余弦相似度可以评价文章的相似度，从而实现对文章，进行分类。

---

K-means

2.1 聚类原理

• 将N个样本映射到k个簇中
• 将每个簇至少有一个样本
  基本思路：
• 先给定k个划分，迭代样本与簇的隶属关系，每次都比前一次好一些
• 迭代若干次就能得到比较好的结果

2.2 K-means 算法原理

算法步骤：

• 选择k个初始的簇中心
• 逐个计算每个样本到簇中心的距离，将样本归属到距离最小的那个簇中心的簇中
• 每个簇内部计算平均值，更新簇中心
• 开始迭代
  
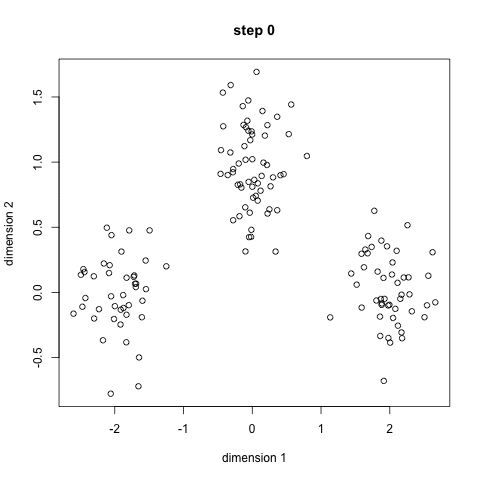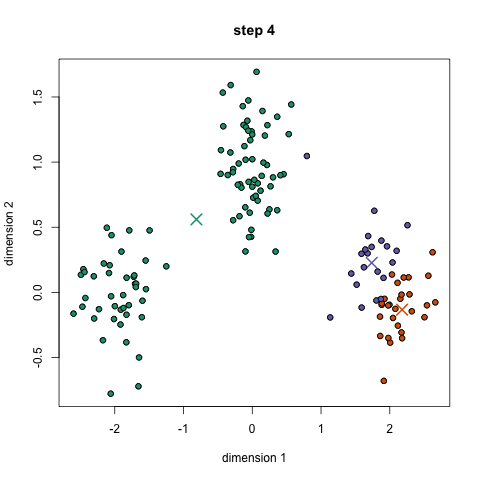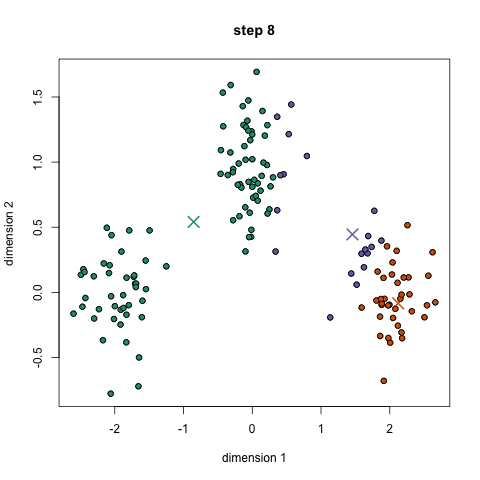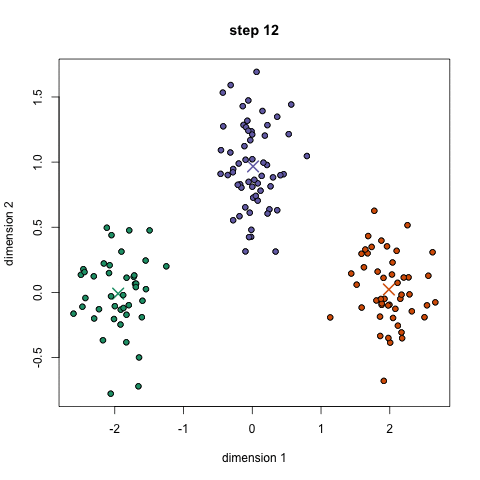
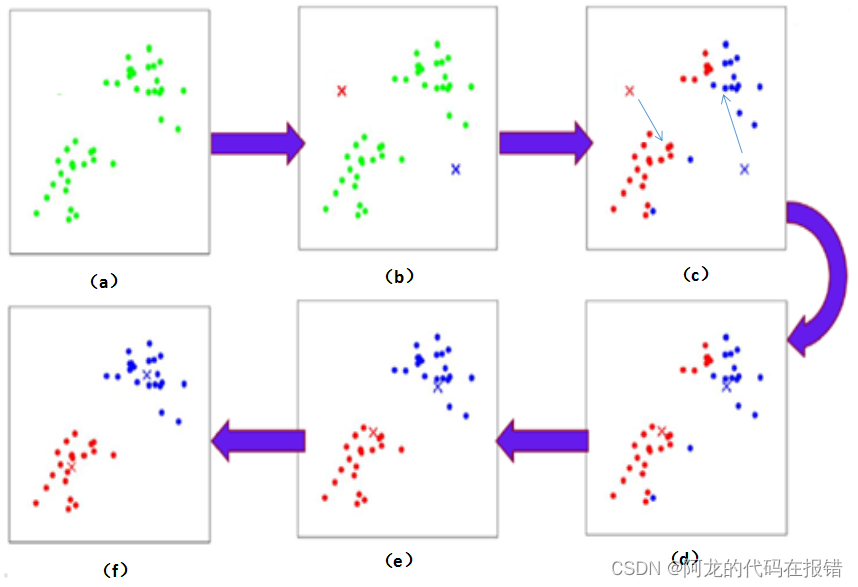
  聚类的过程：
  

2.4 k-means 损失函数

$\sum _{i=0}^n\underset{{\mu }_j\in C}{\min }(||x_i?{\mu }_j|{|}^2)$

• 其中${\mu }_j=\frac{1}{|C_j|}\sum _{x\in C_j}x$ 是簇的均值向量，或者说是质心。

• 其中$||x_i?{\mu }_j|{|}^2$代表每个样本点到均值点的距离（其实也是范数）。

2.5 K-means 执行过程

愿君前程似锦，未来可期去💯,感谢您的阅读，如果对您有用希望您留下宝贵的点赞和收藏
本文章为本人学习笔记，如有请侵权联系，本人会立即删除侵权文章。可以一起学习共同进步谢谢，如有请侵权联系，本人会立即删除侵权文章。