【Image】GAN的超详细解释(以及奇怪的问题)
GAN原理
工作流程
下面是生成对抗网络(GAN)的基本工作原理

在GAN的架构中,有两个关键的组件:生成器(Generator)和鉴别器(Discriminator)。
-
生成器(Generator):其功能是从随机噪声生成数据。在这个上下文中,它试图生成类似于真实数据的新数据。目的是创建足够真实的数据以欺骗鉴别器。
-
鉴别器(Discriminator):它的任务是鉴别输入数据是真实的还是由生成器生成的假数据。简言之,它需要决定输入数据是“真”还是“假”。
工作过程:
- 真实数据会被输入到鉴别器中。
- 同时,生成器产生的数据也会被送入鉴别器。
- 鉴别器会对这两种数据进行分类,将其标记为“真”或“假”。
学习方式:生成器和鉴别器是以对抗的方式进行学习的。生成器试图生成越来越真实的数据来欺骗鉴别器,而鉴别器则试图变得更加精确以区分真实数据和生成的数据。这个过程会不断循环,随着时间的推移,生成器产生的数据会越来越接近真实数据,而鉴别器的判断能力也会越来越强(有点类似于左脚踩右脚原地起飞)。
数学解释
当然,上面的解释只是语言层面的,GAN的原理同样可以从数学上进行解释
min
?
G
max
?
D
V
(
D
,
G
)
=
E
x
~
p
data
(
x
)
[
log
?
D
(
x
)
]
+
E
z
~
p
z
(
z
)
[
log
?
(
1
?
D
(
G
(
z
)
)
)
]
\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_{z}(z)}[\log(1 - D(G(z)))]
Gmin?Dmax?V(D,G)=Ex~pdata?(x)?[logD(x)]+Ez~pz?(z)?[log(1?D(G(z)))]
这是生成对抗网络(GAN)的价值函数,它形式化了生成器 G 和鉴别器 D 之间的对抗游戏。其中 z 指的是上图中的 random noise(虽然这里写的是随机噪声,但是这种噪声往往也是符合某种分布的,一般来说我们认为是高斯分布,最终我们希望这个高斯分布会变成符合真实图像分布的某种分布)。
接下来,我们要非常详细地来解释这个公式

Value函数跟强化学习中的定义一样

一般来说,”真“用1表示;”假“用0表示。所以,当输入是一张”真“图时,我们希望D的值为1;当输入是一张”假“图时,我们希望D的值为0。即D(r) = 1,D(f) = 0。
看图中④的部分,loss = log(D(r))——如果输入是“真”图,这个loss值是0(也就是说如果D(r)能被准确地判断为1,那么“真”图就没有产生任何loss);
看图中⑤的部分,loss = log(1-D(f))——如果输入是“假”图,这个loss值也是0(也就是说如果D(f)能被准确地判断为0,那么“假”图就没有产生任何loss)。
根据log函数特性,在0~1区间内函数最大值为0,所以上式的最大值就是0,在两种情况同时满足时取等。
这也就是为什么,我们希望找到一个很强的D,能够精准分出r和f,并且在这个条件下最大化V。

接下来看到G,我们知道G的目标是要愚弄D,具体就是让D(f) = D(G(z))尽可能被判断为1,这样loss = log(1-D(f)) = -∞.
这就解释了为什么一个是max_D,一个是min_G。

⑦ z~p(z)是噪声分布,即高斯分布
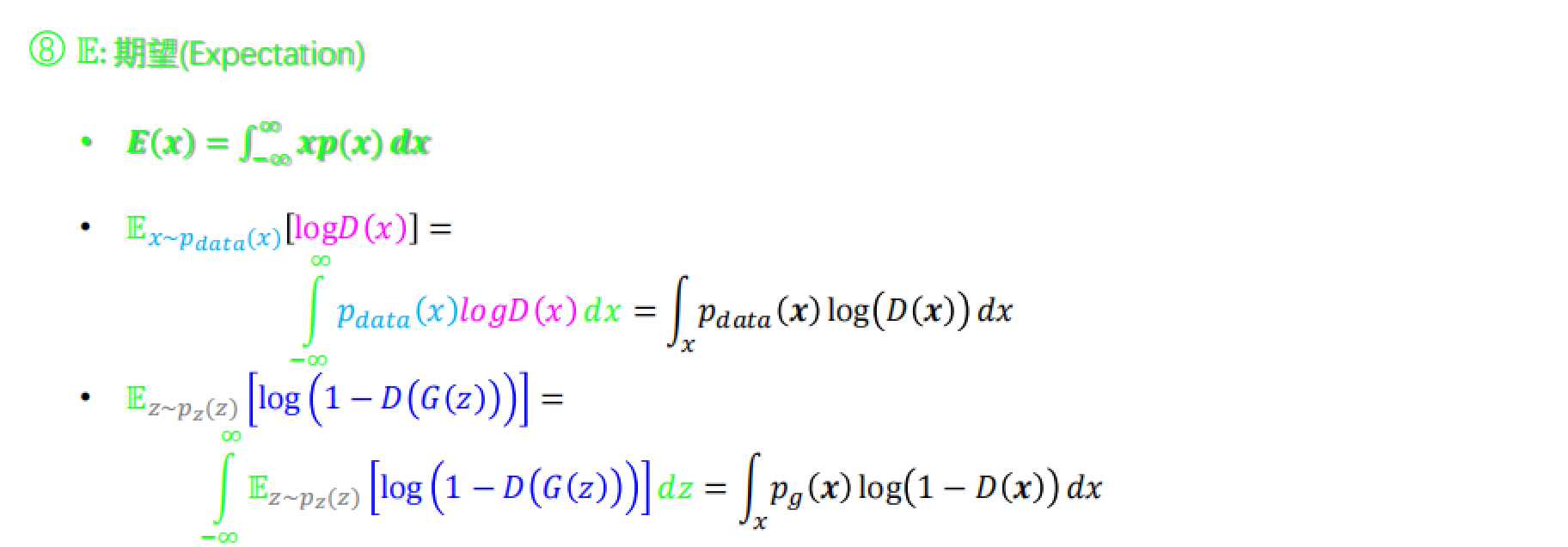
这里计算了期望。
综上所述,上面的公式可以表示为
V
(
D
,
G
)
=
∫
x
p
data
(
x
)
log
?
(
D
(
x
)
)
?
d
x
+
∫
x
p
g
(
x
)
log
?
(
1
?
D
(
x
)
)
?
d
x
=
∫
x
p
data
(
x
)
log
?
(
D
(
x
)
)
+
p
g
(
x
)
log
?
(
1
?
D
(
x
)
)
?
d
x
\begin{align} V(D, G) &= \int_{x} p_{\text{data}}(x) \log(D(x)) \, dx + \int_{x} p_{g}(x) \log(1 - D(x)) \, dx \\ &= \int_{x} p_{\text{data}}(x) \log(D(x)) + p_{g}(x) \log(1 - D(x)) \, dx \end{align}
V(D,G)?=∫x?pdata?(x)log(D(x))dx+∫x?pg?(x)log(1?D(x))dx=∫x?pdata?(x)log(D(x))+pg?(x)log(1?D(x))dx??
这个变换除了带入了期望公式,还做了一个变换——将真实图像与噪声统一成了x,在取值时分别取真实图像和噪声各自对应的分布——在积分中统一了形式,并减少了G。
要求积分最大值,两边求导:
max
?
D
V
(
D
)
=
∫
x
p
data
(
x
)
log
?
(
D
(
x
)
)
+
p
g
(
x
)
log
?
(
1
?
D
(
x
)
)
?
d
x
?
max
?
D
f
(
D
)
=
a
log
?
(
D
)
+
b
log
?
(
1
?
D
)
\max_D V(D) = \int_{x} p_{\text{data}}(x) \log(D(x)) + p_{g}(x) \log(1 - D(x)) \, dx \\\Leftrightarrow \\ \max_D f(D) = a\log(D) + b\log(1 - D) \\
Dmax?V(D)=∫x?pdata?(x)log(D(x))+pg?(x)log(1?D(x))dx?Dmax?f(D)=alog(D)+blog(1?D)
求偏导,解出了D的值使偏导为0,这个D也被称为D*,即最优判别器(Optimal Discriminator)
?
f
?
D
=
a
D
?
b
1
?
D
=
0
?
D
?
=
a
a
+
b
=
p
data
(
x
)
p
data
(
x
)
+
p
g
(
x
)
\frac{\partial f}{\partial D} = \frac{a}{D} - \frac{b}{1 - D} = 0 \Rightarrow D^* = \frac{a}{a + b} = \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{g}(x)}
?D?f?=Da??1?Db?=0?D?=a+ba?=pdata?(x)+pg?(x)pdata?(x)?
然后我们把这个最优判别器带回原式
min
?
G
f
(
G
)
=
∫
x
p
data
(
x
)
log
?
(
2
p
data
(
x
)
p
data
(
x
)
+
p
g
(
x
)
)
?
log
?
2
?
d
x
+
∫
x
p
g
(
x
)
log
?
(
2
p
g
(
x
)
p
data
(
x
)
+
p
g
(
x
)
)
?
log
?
2
?
d
x
=
?
log
?
2
∫
x
p
data
+
p
g
?
d
x
+
∫
x
p
data
log
?
(
2
p
data
p
data
+
p
g
)
?
d
x
+
∫
x
p
g
log
?
(
2
p
g
p
data
+
p
g
)
?
d
x
\min_G f(G) = \int_{x} p_{\text{data}}(x) \log \left( \frac{2p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right) - \log 2 \, dx + \int_{x} p_g(x) \log \left( \frac{2p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right) - \log 2 \, dx\\ = -\log 2 \int_{x} p_{\text{data}} + p_g \, dx + \int_{x} p_{\text{data}} \log \left( \frac{2p_{\text{data}}}{p_{\text{data}} + p_g} \right) \, dx + \int_{x} p_g \log \left( \frac{2p_g}{p_{\text{data}} + p_g} \right) \, dx
Gmin?f(G)=∫x?pdata?(x)log(pdata?(x)+pg?(x)2pdata?(x)?)?log2dx+∫x?pg?(x)log(pdata?(x)+pg?(x)2pg?(x)?)?log2dx=?log2∫x?pdata?+pg?dx+∫x?pdata?log(pdata?+pg?2pdata??)dx+∫x?pg?log(pdata?+pg?2pg??)dx
其中
?
log
?
2
∫
x
p
data
+
p
g
?
d
x
=
?
2
log
?
2
=
?
log
?
4
-\log 2 \int_{x} p_{\text{data}} + p_g \, dx = -2\log2 = -\log4
?log2∫x?pdata?+pg?dx=?2log2=?log4
散度 Divergence
讲到这里我们穿插一下散度 (Divergence) 的概念:"Divergence"是一种度量或评估两个概率分布差异的方法,它被用来比较两个分布之间的不同程度,可以帮助我们了解一个分布如何或在何种程度上不同于另一个分布。
KL散度(Kullback-Leibler Divergence)
KL?-?Divergence: D K L ( P ∥ Q ) = ∑ i P ( i ) log ? ( P ( i ) Q ( i ) ) = ∫ x P ( x ) log ? ( P ( x ) Q ( x ) ) d x \text{KL - Divergence:} \quad D_{KL}(P \parallel Q) = \sum_i P(i)\log\left(\frac{P(i)}{Q(i)}\right) = \int_{x} P(x)\log\left(\frac{P(x)}{Q(x)}\right) dx KL?-?Divergence:DKL?(P∥Q)=i∑?P(i)log(Q(i)P(i)?)=∫x?P(x)log(Q(x)P(x)?)dx
- KL散度是衡量两个概率分布P和Q差异的非对称度量。具体来说,它衡量的是,当使用概率分布Q来近似真实分布P时,所损失的信息量。
- 它是从信息论的视角出发的,基于信息熵的概念,其中P是真实分布,Q是模型的预测分布。
- 一个重要的特性是非对称性,即
D K L ( P ∥ Q ) ≠ D K L ( Q ∥ P ) D_{KL}(P \parallel Q) \neq D_{KL}(Q \parallel P) DKL?(P∥Q)=DKL?(Q∥P)
这也是KL散度的一个明显的缺陷,因为分布是没有方向性的。
JS散度(Jensen-Shannon Divergence)
JS?-?Divergence: J S D ( P ∥ Q ) = 1 2 D K L ( P ∥ P + Q 2 ) + 1 2 D K L ( Q ∥ P + Q 2 ) \text{JS - Divergence:} \quad JSD(P \parallel Q) = \frac{1}{2}D_{KL}\left(P \parallel \frac{P+Q}{2}\right) + \frac{1}{2}D_{KL}\left(Q \parallel \frac{P+Q}{2}\right) JS?-?Divergence:JSD(P∥Q)=21?DKL?(P∥2P+Q?)+21?DKL?(Q∥2P+Q?)
- JS散度是KL散度的对称版本,它衡量两个概率分布P和Q的相似性,并且总是有界的(在0和1之间)。
- 它的计算方式是取两个分布P和Q相对于它们的平均值的KL散度的平均值。
- 因为JS散度是对称的,所以它通常被认为是两个分布之间距离的更好的度量。
如此一来,我们用JS散度对上面的公式进行替换,得到
min ? G f ( G ) = ∫ x p data ( x ) log ? ( 2 p data ( x ) p data ( x ) + p g ( x ) ) ? log ? 2 ? d x + p g ( x ) log ? ( 2 p g ( x ) p data ( x ) + p g ( x ) ) ? log ? 2 ? d x = ? log ? 2 ∫ x p data + p g ? d x + 2 J S D ( p data ∥ p g ) = ? log ? 4 + 2 J S D ( p data ∥ p g ) ≥ ? log ? 4 , where? [ p d a t a = p g ] \min_G f(G) = \int_{x} p_{\text{data}}(x) \log \left( \frac{2p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right) - \log 2 \, dx + p_g(x) \log \left( \frac{2p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right) - \log 2 \, dx\\ = -\log 2 \int_{x} p_{\text{data}} + p_g \, dx + 2JSD(p_{\text{data}} \parallel p_g)\\ = -\log 4 + 2JSD(p_{\text{data}} \parallel p_g)\\ \geq -\log 4, \quad \text{where } [p_{data} = p_g] Gmin?f(G)=∫x?pdata?(x)log(pdata?(x)+pg?(x)2pdata?(x)?)?log2dx+pg?(x)log(pdata?(x)+pg?(x)2pg?(x)?)?log2dx=?log2∫x?pdata?+pg?dx+2JSD(pdata?∥pg?)=?log4+2JSD(pdata?∥pg?)≥?log4,where?[pdata?=pg?]
这就是上面的minmax函数的最简表达形式。
Summary
-
Generate a discriminator (D) & a generator (G) step by step
-
The target of the D is to try its best to discriminate real and fake images while the target of the G is to try its best to generate fake images to fool the D.
-
It seems we can get a global optimality (equilibrium) by dragging 𝒑𝒈 → 𝒑𝒅𝒂𝒕𝒂
奇怪的问题
但是,现在我们这个公式有一个很大的问题。
下面先给出一个mnist生成数字的GAN代码
# dataset: mnist
import argparse
import os
import numpy as np
import math
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch
from generator import Generator
from discriminator import Discriminator
os.makedirs("images", exist_ok=True)
parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=64, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.0002, help="adam: learning rate")
parser.add_argument("--b1", type=float, default=0.5, help="adam: decay of first order momentum of gradient")
parser.add_argument("--b2", type=float, default=0.999, help="adam: decay of first order momentum of gradient")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples")
opt = parser.parse_args()
print(opt)
# 图像的形状参数
img_shape = (opt.channels, opt.img_size, opt.img_size)
# 定义损失函数为二元交叉熵损失
adversarial_loss = torch.nn.BCELoss()
# 初始化生成器和鉴别器
generator = Generator()
discriminator = Discriminator()
# 如果CUDA可用,将网络和损失函数移动到GPU
cuda = True if torch.cuda.is_available() else False
if cuda:
generator.cuda()
discriminator.cuda()
adversarial_loss.cuda()
# 配置数据加载器
os.makedirs("./data/mnist", exist_ok=True)
dataloader = torch.utils.data.DataLoader(
datasets.MNIST(
"./data/mnist",
train=True,
download=True,
# 数据预处理:调整大小、转换为张量、标准化
transform=transforms.Compose(
[transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5])]
),
),
batch_size=opt.batch_size,
shuffle=True,
)
# 配置优化器,使用Adam优化器
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
# 根据CUDA环境选择数据类型
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
# 开始训练
for epoch in range(opt.n_epochs):
for i, (imgs, _) in enumerate(dataloader):
# Adversarial ground truths
# 创建标签数据:真实图片的标签为1,生成图片的标签为0
valid = Tensor(imgs.size(0), 1).fill_(1.0).detach()
fake = Tensor(imgs.size(0), 1).fill_(0.0).detach()
# 配置输入
real_imgs = imgs.type(Tensor)
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad() # 对已有的gradient清零(因为来了新的batch_size的image)
z = Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))) # 随机生成输入噪声
gen_imgs = generator(z) # 生成一个batch的假图片
# Loss measures generator's ability to fool the discriminator
g_loss = adversarial_loss(discriminator(gen_imgs), # D(G(z))
valid) # label = 1, 这里将假图的label置为1的原因下一篇文章会说
g_loss.backward() # bp, 算gradient, x.grad += dloss/dx
optimizer_G.step() # 更新x, x -= lr * x.grad
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
real_loss = adversarial_loss(discriminator(real_imgs), # D(x)
valid) # lable = 1
fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), # D(G(z)), 这里用到detach的原因是:gen_imgs后面带着generator的参数,而这里训练的是discriminator的参数
fake) # lable = 0
d_loss = (real_loss + fake_loss) / 2 # 计算鉴别器的总损失
d_loss.backward() # bp, 算gradient, x.grad += dloss/dx
optimizer_D.step() # 更新x, x -= lr * x.grad
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
)
# 每隔一定的间隔保存生成的图片
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
generator.py
import torch.nn as nn
import numpy as np
# 定义生成器输入的噪声向量的维度和生成图像的形状
latent_dim = 100
img_shape = (1, 28, 28)
# 定义Generator类,继承自nn.Module
class Generator(nn.Module):
# 初始化函数
def __init__(self):
super(Generator, self).__init__() # 调用父类的构造函数
# 定义一个block函数用于构建神经网络的层,其中包含线性层,可选的批标准化层和LeakyReLU激活函数
def block(in_feat, out_feat, normalize=True):
layers = [nn.Linear(in_feat, out_feat)] # 线性层
if normalize:
# 如果normalize为True,则添加批标准化层
layers.append(nn.BatchNorm1d(out_feat, 0.8))
# 添加LeakyReLU激活函数,其中negative_slope(斜率)设置为0.2
layers.append(nn.LeakyReLU(0.2, inplace=True))
return layers # 返回构建的层列表
# 使用Sequential模块将所有层堆叠成一个完整的模型
self.model = nn.Sequential(
*block(latent_dim, 128, normalize=False), # 第一层不进行批标准化
*block(128, 256), # 后续层逐渐增加输出特征的维度
*block(256, 512),
*block(512, 1024),
# 最后一层是一个线性层,它的输出大小与图像大小的乘积相同
nn.Linear(1024, int(np.prod(img_shape))),
nn.Tanh() # 使用Tanh激活函数将输出值限制在[-1,1]之间,因为图像数据通常归一化到这个范围
)
# 前向传播函数定义了模型如何从输入产生输出
def forward(self, z):
img = self.model(z) # 使用model生成图像数据
# 调整输出的形状,使其与目标图像形状一致
img = img.view(img.size(0), *img_shape)
return img # 返回生成的图像
discriminator.py
import torch.nn as nn
import numpy as np
# 图像的形状参数
img_shape = (1, 28, 28)
# 定义Discriminator类,继承自nn.Module
class Discriminator(nn.Module):
# 初始化函数
def __init__(self):
super(Discriminator, self).__init__() # 调用父类的构造函数
# 构建鉴别器的神经网络模型,使用Sequential容器
self.model = nn.Sequential(
# 输入层,将输入向量的维度从图像形状展平为一维向量
nn.Linear(int(np.prod(img_shape)), 512),
# 使用LeakyReLU作为激活函数,其斜率设置为0.2
nn.LeakyReLU(0.2, inplace=True),
# 中间层,继续减少特征的维度
nn.Linear(512, 256),
# 同样使用LeakyReLU激活函数
nn.LeakyReLU(0.2, inplace=True),
# 输出层,将特征压缩为一个单一的预测值
nn.Linear(256, 1),
# 使用Sigmoid激活函数将输出值压缩到[0,1]之间,作为真假图像的概率
nn.Sigmoid(),
)
# 前向传播函数定义了模型如何从输入产生输出
def forward(self, img): # img.shape = torch.Size([64, 1, 28, 28]) = 64 * 1 * 28 * 28
# 将输入图像展平为一维向量
img_flat = img.view(img.size(0), -1) # (64, -1 = 1 * 28 * 28)
# 将展平的图像向量传递给模型,并得到有效性预测
validity = self.model(img_flat)
return validity # 返回预测的有效性(即图像为真实图像的概率)

然而,看看最后生成的结果

我们初始的噪声其实是很不一样的,但是一个非常奇怪的现象是——我们最后确实又生成了很多一样的东西。甚至,二行四列和三行四列(或者二行二列和五行三列)的两个明显是生成错了,但即便是错也是错得十分相似。
这其中的问题还是挺严重的。欲知后事如何,且听下回分解~
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!