模式识别与机器学习-无监督学习-降维

谨以此博客作为复习期间的记录

为什么要降维

1. 消除冗余信息和噪声： 原始数据集可能包含大量冗余特征或噪声，这些特征可能对模型训练产生负面影响。通过降维，可以剔除不相关或冗余的特征，提高模型的泛化能力。

2. 简化模型复杂度： 较高维度的数据会增加模型的复杂性和计算成本。降低数据维度可以减少模型训练和预测的时间，使得模型更加高效。

3. 避免维度灾难： 在高维空间中，数据变得稀疏，样本间的距离变得很大，导致模型性能下降。降维有助于缓解维度灾难问题，提高模型的性能和准确性。

4. 可视化和理解数据： 降维可以将高维数据映射到二维或三维空间，使其更易于可视化展示和理解。这有助于发现数据之间的潜在关系和模式。

降维方法主要分为两大类：特征选择和特征提取。特征选择是指直接选择重要特征，舍弃不重要的特征；而特征提取则是通过线性变换等数学方法，将原始特征映射到一个新的低维度空间。

维度选择

手工移除特征

以下这些特征可能需要手工移除。

• 质量差的特征（特征的缺失比例超过50%）
• 冗余的（multicollinearity/方差膨胀因子VIF）
• 不相关（文本挖掘中的停用词）

过滤式选择

过滤式选择（Filter Feature Selection）是一种常见的降维方法，其基本原理是在训练模型之前，通过对特征进行评估和排序，选择最具信息量的特征子集。它不依赖于任何特定的机器学习模型，而是根据特征本身的统计性质或相关性来进行特征选择。

以下是过滤式选择的一般步骤：

1. 特征评估： 针对每个特征，使用统计方法进行评估，确定其与目标变量之间的相关性或信息量。常用的评估指标包括信息增益、方差、相关系数等。

2. 特征排序： 对特征进行排序，按照其评估得分高低进行排列。通常，选择具有较高分数的特征作为最终的特征子集。

3. 特征选择： 根据预先设定的阈值或选择前N个特征的方式，从排好序的特征列表中选择要保留的特征。这些特征将作为输入用于后续的模型训练。

过滤式选择的优点包括：

• 计算效率高： 在数据预处理阶段就完成了特征选择，避免了在模型训练中进行特征筛选的计算开销。
• 模型无关性： 不依赖于具体的机器学习模型，因此适用于各种算法和任务。
• 简单直观： 通常易于理解和实现。

然而，过滤式选择也存在一些限制：

• 忽略特征之间的关联性： 它只考虑单个特征与目标变量之间的关系，可能忽略了特征之间的复杂关联。
• 不考虑后续模型的性能： 选择特征时不考虑模型本身的性能，可能导致选择的特征并不是最优的，不能保证在后续模型中获得最佳性能。

包裹式选择

包裹式选择（Wrapper Feature Selection）是一种特征选择方法，与过滤式选择不同，它将特征选择看作是一个子集搜索问题，并使用特定的机器学习模型来评估每个特征子集的性能。这种方法依赖于所选模型的性能来评估特征子集的好坏。

基本上，包裹式选择的工作流程如下：

1. 特征子集搜索： 从原始特征集合中生成不同的特征子集（组合），这些子集可能包含不同数量的特征。

2. 模型训练和评估： 使用选定的机器学习模型对每个特征子集进行训练，并评估模型在验证集或交叉验证中的性能。

3. 选择最佳特征子集： 根据模型性能选择最佳的特征子集作为最终的特征组合。

4. 应用于测试集： 使用选定的特征子集对测试数据进行预测或分类。

包裹式选择的优点包括：

• 考虑特征之间的关联性： 通过搜索特征子集，能够考虑到特征之间的相互作用和关联。
• 最大化模型性能： 选择特征子集时直接使用模型评估性能，可以更好地适应所选择的机器学习模型。

然而，包裹式选择也存在一些缺点：

• 计算开销大： 由于需要训练多个模型来评估不同的特征子集，因此计算成本通常较高。
• 过度拟合风险： 在搜索特征子集时，可能会过度拟合训练集，导致所选择的特征子集在其他数据集上泛化能力较差。

常见的包裹式选择方法包括递归特征消除（Recursive Feature Elimination，RFE）和正向选择（Forward Selection）等。选择适当的包裹式方法需要根据数据集的大小、特征数量、计算资源和模型性能等因素进行权衡考虑。

嵌入式选择

嵌入式选择（Embedded Feature Selection）与过滤式选择和包裹式选择不同，它将特征选择与模型训练过程结合在一起，通过在模型训练过程中自动选择最佳特征。

在嵌入式选择中，特征选择过程与模型训练过程是紧密耦合的。它使用具有内置特征选择机制的机器学习算法，这些算法能够在训练过程中自动学习和选择最相关的特征。通常，这些方法会根据特征的权重或重要性来决定特征的贡献程度，并且会剔除对模型不重要的特征。

嵌入式选择的主要优点包括：

• 自动特征选择： 在模型训练过程中自动选择最优的特征，不需要额外的特征评估步骤。
• 结合模型优化： 能够充分利用模型自身的优化过程，提高了特征选择的准确性。
• 减少过拟合风险： 通过同时考虑特征和模型，可以减少过拟合的风险，提高模型的泛化能力。

一些典型的嵌入式选择方法包括：

• Lasso回归（套索回归）： 使用L1正则化项来推动模型系数稀疏化，从而实现特征选择。
• 决策树和基于树的方法： 如随机森林、梯度提升树等，它们可以通过特征的重要性来进行特征选择。
• 支持向量机（SVM）： 在SVM中，支持向量和相关的特征对分类或回归任务具有重要性，因此可以用于特征选择。

维度抽取（线性模型）

MDS

多维尺度（Multidimensional Scaling，MDS）是一种经典的降维技术，用于将高维数据映射到低维空间。其主要目标是保持数据点之间的距离或相似性关系，以便在降维后的空间中尽可能地保留原始数据的结构和信息。

MDS可以分为两种类型：度量MDS和非度量MDS。

1. 度量MDS（Metric MDS）： 在度量MDS中，尝试在低维空间中保持数据点之间的距离关系。这意味着，如果两个数据点在高维空间中距离较远，那么在低维空间中它们仍然应该保持一定的距离。常用的距离度量包括欧氏距离、曼哈顿距离等。

2. 非度量MDS（Non-metric MDS）： 非度量MDS关注于保持数据点之间的相对顺序而不是具体的距离值。它基于数据点之间的相似性或相对关系来进行降维。这种方法在不知道准确距离值的情况下，尤其有用。

MDS的工作流程通常包括以下步骤：

• 计算相似性/距离矩阵： 根据原始高维数据计算数据点之间的距离或相似性，这可以是欧氏距离、相关系数、余弦相似度等。

• 降维： 在得到距离或相似性矩阵后，MDS算法将数据点映射到一个低维空间中，以保持尽可能多的原始数据点之间的距离或相似性关系。

• 优化过程： MDS通过迭代优化过程来调整数据点在低维空间中的位置，以最大程度地满足在高维空间中的相似性关系。

PCA

PCA的主要目标是通过线性变换将原始特征投影到一个新的特征空间，这个新的特征空间是原始特征的线性组合。PCA将数据的方差最大化，通过保留最大方差的特征来减少数据集的维度。

PCA的工作流程如下：

PCA的优点包括：

• 降低数据维度： 可以减少数据集的维度，提高计算效率。
• 保留主要信息： 保留数据中最重要的信息，最大程度地保持原始数据的方差。
• 去相关化： 通过主成分，去除原始数据特征之间的相关性。

然而，PCA也存在一些限制：

• 线性变换限制： PCA是基于线性变换的，可能无法捕捉数据中的非线性关系。
• 可能信息丢失： 低维空间中的特征是原始特征的线性组合，可能会导致一些信息丢失。

PCA有两个非常核心的思想，最小重构误差和最大投影方差，从这两个思想出发都可以推到得到PCA的形式。

目标1：最小重构误差

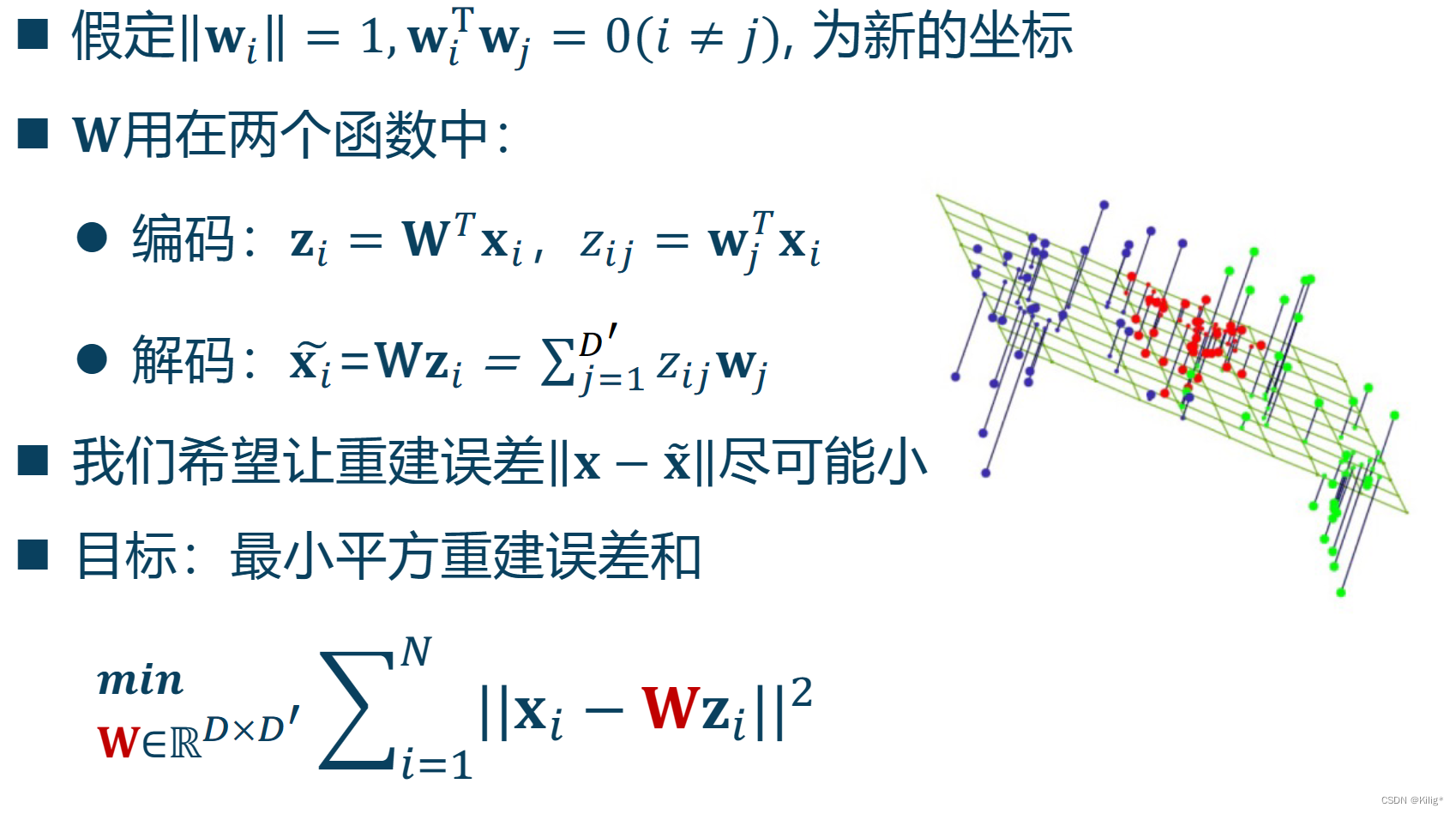
目标2：最大投影方差

SVD

奇异值分解（Singular Value Decomposition，SVD）是一种矩阵分解技术，可以将一个矩阵分解为三个矩阵的乘积，用于降低数据的维度和特征提取。对于给定的一个 $m\times n$ 的矩阵 $A$，其SVD表示为：

$$A=U\Sigma V^T$$

其中：

• $U$ 是一个 $m\times m$ 的正交矩阵，其列向量是$A{A}^T$的特征向量。
• $\Sigma$ 是一个 $m\times n$ 的对角矩阵，其对角线上的元素称为奇异值，表示了矩阵 $A$ 的奇异值。
• $V$ 是一个 $n\times n$ 的正交矩阵，其列向量是$A^{T}A$的特征向量。

对于矩阵 $A$，其奇异值分解可以用于降低维度。通常，通过保留最重要的奇异值（即最大的奇异值），可以获得一个低秩近似矩阵，从而实现降维。

具体进行SVD的计算步骤如下：

1. 计算 $A^{T}A$ 或 $A{A}^T$： 首先，计算矩阵 $A$ 与其转置的乘积 $A^{T}A$ 或 $A{A}^T$（取决于 $A$ 的大小）。

2. 求解特征值与特征向量： 对于 $A^{T}A$ 或 $A{A}^T$，求解其特征值和特征向量。这些特征值和特征向量将用于后续步骤。

3. 选择奇异值与奇异向量： 通过特征值和特征向量得到矩阵 $A$ 的奇异值和对应的左奇异向量和右奇异向量。

4. 构建奇异值分解矩阵： 将奇异值按降序排列构建成对角矩阵 $\Sigma$，左奇异向量构成矩阵 $U$，右奇异向量构成矩阵 $V$。

下面是使用Python中NumPy库进行SVD分解的示例代码：

import numpy as np

# 假设有一个矩阵 A
A = np.array([[1, 2, 3], [4, 5, 6]])

# 进行SVD分解
U, S, VT = np.linalg.svd(A)

# U、S、VT分别为左奇异矩阵、奇异值对角矩阵、右奇异矩阵的转置
print("左奇异矩阵 U：")
print(U)
print("\n奇异值对角矩阵 S：")
print(np.diag(S))
print("\n右奇异矩阵的转置 VT：")
print(VT)

思考：为什么保留特征值大的？

在PCA降维或者SVD降维中，保留特征值（PCA）或奇异值（SVD）大的原因与信息量和方差的关系有关。

1. 方差和信息量： 特征值（PCA）或奇异值（SVD）代表了数据在特征方向上的方差或重要性。较大的特征值或奇异值意味着数据在相应特征方向上的方差较大，即数据在这个方向上的变化程度较大。

2. 信息捕获： 在降维过程中，保留较大的特征值或奇异值相当于保留了数据中方差较大的方向，即保留了最重要的特征或信息。这些方差大的方向代表了数据中最主要的变化模式或特征，因此保留它们有助于保持数据的重要信息。

3. 维度压缩： 通过保留较大的特征值或奇异值，可以实现对数据的维度压缩，同时尽可能地保留了最重要的特征信息。这种降维方式可以减少数据中不重要的噪声或变化不明显的方向，从而更有效地表达数据的主要特征。

总的来说，特征值或奇异值越大，代表着数据在对应方向上的信息量越大，因此在降维时保留这些特征值或奇异值大的方向，可以更好地保留数据的主要特征和重要信息，有助于更有效地表示原始数据。

维度抽取（非线性模型）

上一部分的线性模型在遇到非线性降维情况时，往往效果没那么理想。就像下图这样。因此有必要使用一些非线性的降维方法来达到更好的效果。

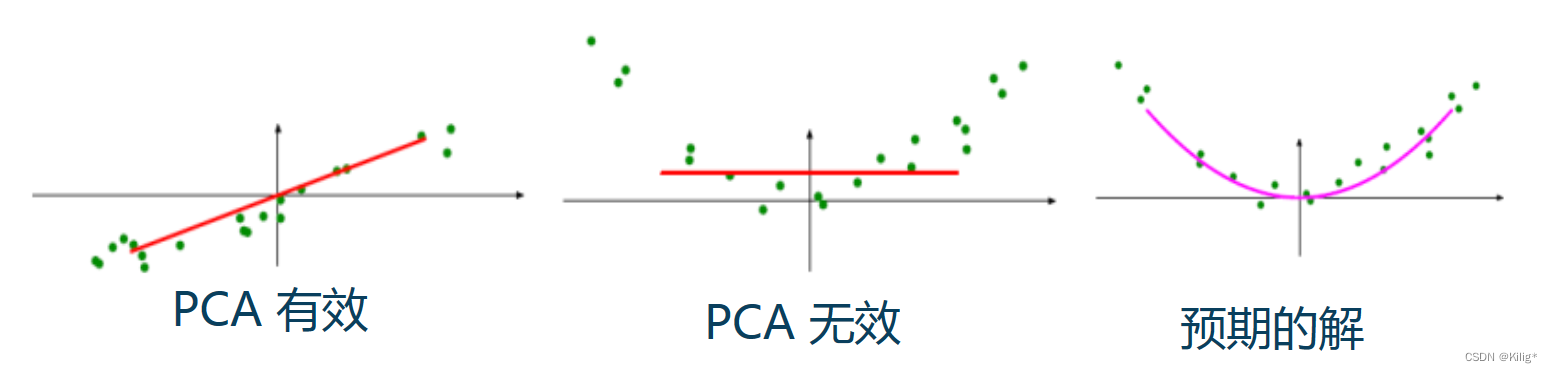
KPCA

核主成分分析（Kernel Principal Component Analysis，KPCA）是主成分分析（PCA）的非线性扩展，它利用核技巧将非线性数据映射到高维空间，从而实现对非线性数据的降维。

原理如下：

1. 非线性映射： 使用核技巧（如多项式核、高斯核等）将原始数据映射到一个更高维的特征空间，使得数据在该特征空间中可以更容易地被线性分离或线性表示。

2. PCA在高维空间： 在高维特征空间中，执行标准的PCA，寻找能够最大化数据方差的主成分。

3. 降维： 选择最重要的主成分投影到原始空间中，从而实现对非线性数据的降维。

核函数在KPCA中起着关键作用，它们可以将数据隐式地映射到高维空间，而无需显式计算高维空间的特征向量。常用的核函数包括线性核、多项式核、高斯径向基函数（RBF）核等。选择适当的核函数对KPCA的性能和效果至关重要。

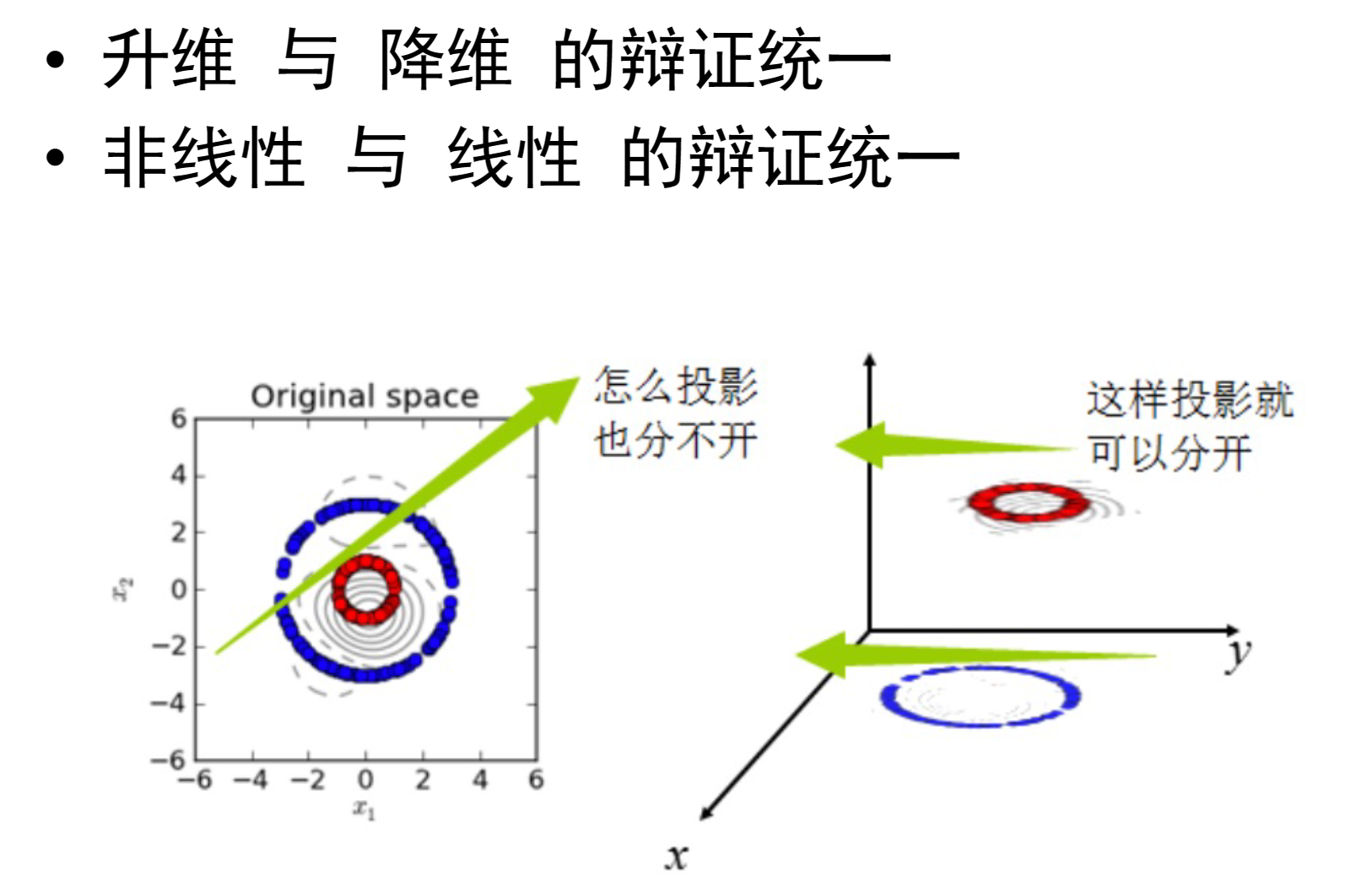
流形学习

为什么要有流形学习呢？原因如下图:

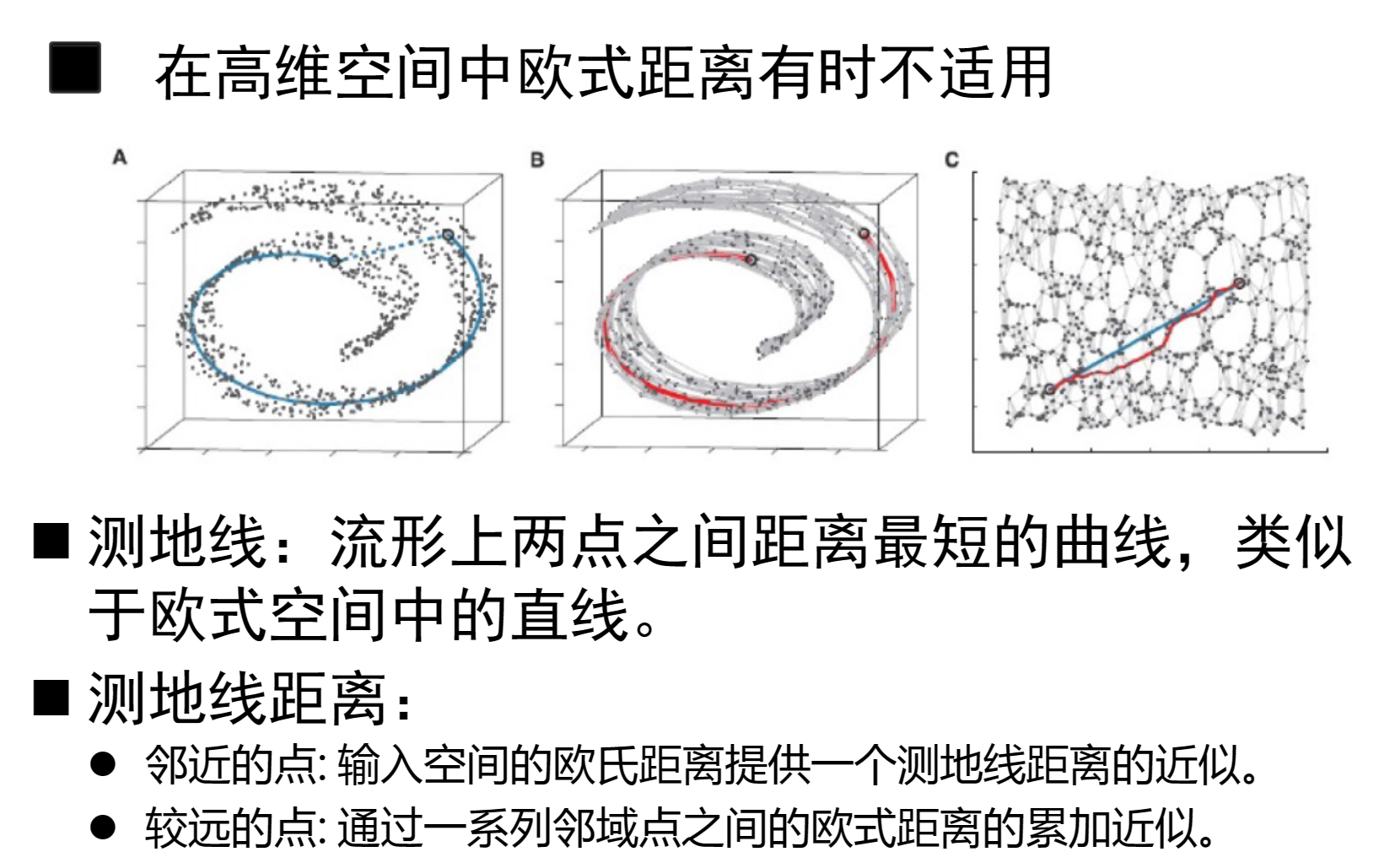
ISOMAP

优点：

1. 保持数据流形结构： ISOMAP试图保持数据点之间的地理距离关系，能够更好地捕捉数据的非线性结构。

2. 降维后保持拓扑结构： ISOMAP在降维过程中努力保持数据点之间的拓扑结构，使得在降维后仍能保持数据之间的相对距离关系。

3. 适用于曲面结构数据： ISOMAP适用于处理具有曲面结构或复杂非线性结构的数据，如人脸图像、地理数据等。

缺点：

1. 计算复杂度高： ISOMAP需要计算数据点之间的距离矩阵，因此在大规模数据集上的计算成本较高，随着数据量增加，计算复杂度呈二次增长。

2. 对噪声敏感： ISOMAP对噪声和局部数据分布的变化较为敏感，可能受到异常点的影响。

3. 依赖于距离计算： ISOMAP对于距离的计算十分关键，如果数据间的距离计算不准确或不恰当，会影响最终的降维效果。

4. 维度灾难问题： ISOMAP在高维数据上也会受到维度灾难的影响，因为在高维空间中计算距离会受到维度的限制。

LLE

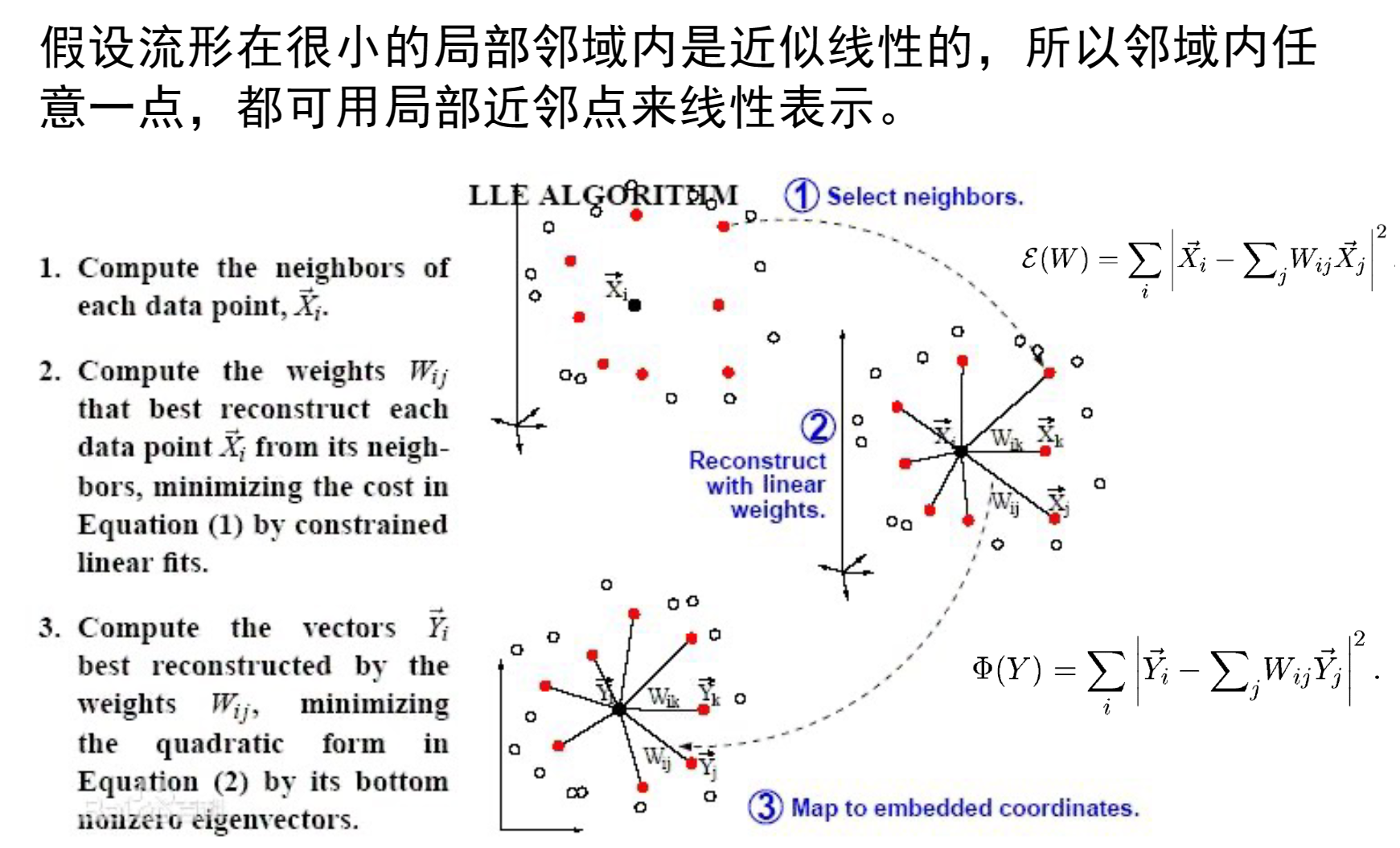
局部线性嵌入（Locally Linear Embedding，LLE）是一种非线性降维技术，用于将高维数据映射到一个低维空间，同时保持数据的局部线性结构。LLE的目标是在降维后保持邻近数据点之间的局部关系和流形结构。

LLE的主要思想是：对于每个数据点，通过局部线性组合近邻数据点来重构该点，从而保持局部关系不变。它具体的工作步骤如下：

1. 近邻选择： 对于每个数据点，通过一定的近邻选择方式（如最近邻方法），找到其局部近邻数据点。

2. 局部重构权重： 对于每个数据点，通过最小化其与邻近数据点的线性重构误差，计算得到一个权重系数，用于对其进行局部线性重构。（优化$w$）

3. 低维表示： 通过优化局部重构权重，将高维数据点映射到低维空间，并尽可能保持局部线性关系。(优化$y$)

T-SNE

T分布随机邻域嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）是一种流行的非线性降维和数据可视化技术，用于将高维数据映射到一个低维空间（通常是2维或3维），以便于观察和分析数据的结构。

t-SNE的主要目标是保持数据点之间的局部相似性关系，尤其是在高维空间中保持那些局部密集的数据点之间的相对距离关系，同时尽可能地降低那些在高维空间中相对较远的数据点之间的距离。这有助于在降维后更好地呈现数据点之间的固有结构。

t-SNE的工作原理可以简述如下：

1. 构建相似性矩阵： 首先，t-SNE计算原始高维数据点之间的相似性，通常使用高斯核函数来衡量点与点之间的相似度。

2. 降维： t-SNE通过优化的方式，尝试在低维空间中重建相似性矩阵，使得低维空间中的数据点能够尽可能地反映出高维空间中数据点的局部相似性关系。

3. 梯度下降优化： t-SNE使用梯度下降或其他优化方法来最小化高维空间中的相似性矩阵与低维空间中的相似性矩阵之间的差异。

t-SNE的优点和特点包括：

• 保留局部结构： t-SNE注重保留数据点之间的局部结构，能够很好地展现数据集中密集和稀疏区域的差异。

• 可视化效果好： t-SNE在数据可视化方面效果很好，能够帮助人们更直观地观察数据的固有结构和聚类。

• 适用于高维数据： 对于高维数据集，t-SNE能够较好地将其映射到低维空间中，并保持数据结构的特性。

然而，t-SNE也有一些局限性：

• 计算复杂度高： t-SNE的计算复杂度较高，尤其是对于大规模数据集，运行时间较长。

• 随机性： t-SNE的结果可能会因初始化和参数设置而有所不同，不同的随机种子可能导致不同的降维结果。

t-SNE通常用于数据探索和可视化，有助于理解高维数据的内在结构，但在实际应用中需要考虑其计算成本和参数调优等问题。