D51+D52|接雨水
503.下一个更大元素ll
初始思路:这样这道题就变成了一道很纯粹的单调栈问题,因为只涉及了一个数组。但又因为这个数组是一个循环数组所以问题又变的有些复杂。
初始思路:
在循环数组的问题中,比较需要考虑的就是数组中最后一个数字出现在数组头部的问题,所以考虑将创建一个新数组,数组中的元素为原数组元素+数组中最后一个数组前的元素,然后使用基本单调栈的方法处理该问题。answer数组和原数组大小相同。
class Solution {
public int[] nextGreaterElements(int[] nums) {
int[] ans = new int[nums.length];
Arrays.fill(ans,-1);
int[] newnums = new int[2*nums.length-1];
for(int i = 0;i<newnums.length;i++){
if(i<nums.length){
newnums[i] = nums[i];
}else{
newnums[i] = nums[i-nums.length];
}
}
Stack<Integer> st = new Stack<>();
st.push(0);
for(int i = 1;i<newnums.length;i++){
if(newnums[i]<=newnums[st.peek()]){
st.push(i);
}else{
while(!st.isEmpty()&&newnums[i]>newnums[st.peek()]){
int pos = st.peek()<nums.length?st.peek():st.peek()-nums.length;
ans[pos] = newnums[i];
st.pop();
}
st.push(i);
}
}
return ans;
}
}题解复盘:
直接使用取余操作代替填充数组!!
class Solution {
public int[] nextGreaterElements(int[] nums) {
//边界判断
if(nums == null || nums.length <= 1) {
return new int[]{-1};
}
int size = nums.length;
int[] result = new int[size];//存放结果
Arrays.fill(result,-1);//默认全部初始化为-1
Stack<Integer> st= new Stack<>();//栈中存放的是nums中的元素下标
for(int i = 0; i < 2*size; i++) {
while(!st.empty() && nums[i % size] > nums[st.peek()]) {
result[st.peek()] = nums[i % size];//更新result
st.pop();//弹出栈顶
}
st.push(i % size);
}
return result;
}
}42.接雨水?
初始思路&&题解复盘:
大概能理解雨水的数量是如何计算出来的,但是找到一套通用的计算公式还是比较困难的。

单调栈是按照行方向来计算雨水的。
以下逻辑主要就是三种情况
- 情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
- 情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
- 情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
先将下标0的柱子加入到栈中,st.push(0);。 栈中存放我们遍历过的元素,所以先将下标0加进来。
然后开始从下标1开始遍历所有的柱子,for (int i = 1; i < height.size(); i++)。
如果当前遍历的元素(柱子)高度小于等于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:

取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的元素,三个元素来接水!
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:int h = min(height[st.top()], height[i]) - height[mid];
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:int w = i - st.top() - 1 ;
当前凹槽雨水的体积就是:h * w。
class Solution {
public int trap(int[] height) {
Stack<Integer> st = new Stack<>();
st.push(0);
int res = 0;
int mid = 0;
int h = 0;
int weight = 0;
for( int i = 1;i<height.length;i++){
if(height[i]<=height[st.peek()]){
st.push(i);
}else{
while(!st.isEmpty()&&height[i]>height[st.peek()]){
mid = height[st.pop()];
if(!st.isEmpty()){
h = Math.min(height[i],height[st.peek()])-mid;
weight = i-st.peek()-1;
res = res +h*weight;
}
}
st.push(i);
}
}
return res;
}
}84.柱状图中最大的矩形
同上:如何在单调栈的规律中找到求最大矩形的计算规律是一个有点想不明白的问题。
初始思路&&题解复盘:

只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
所以本题单调栈的顺序正好与接雨水反过来。
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度(理解如何由单调栈问题思考出计算最大面积的方式)
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);理解为什么在首尾均需要添加0元素。
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:

那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑。
开头为什么要加元素0?
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left。
(mid、left,right 都是对应版本一里的逻辑)
因为 将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑。
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 8 进行比较,周而复始,那么计算的最后结果resutl就是0。 如图所示:

所以我们需要在 height数组前后各加一个元素0。
添加0元素部分代码:
int[] newHeight = new int[heights.length + 2];
System.arraycopy(heights, 0, newHeight, 1, heights.length);
newHeight[heights.length+1] = 0;
newHeight[0] = 0;System.arraycopy(int[] arr, int star,int[] arr2, int start2, length);
5个参数,
第一个参数是要被复制的数组
第二个参数是被复制的数字开始复制的下标
第三个参数是目标数组,也就是要把数据放进来的数组
第四个参数是从目标数据第几个下标开始放入数据
第五个参数表示从被复制的数组中拿几个数值放到目标数组中
?
class Solution {
public int largestRectangleArea(int[] heights) {
int[] newheights = new int[heights.length+2];
System.arraycopy(heights,0,newheights,1,heights.length);
newheights[0] = 0;
newheights[newheights.length-1] = 0;
Stack<Integer> st = new Stack<>();
st.push(0);
int res = 0;
for(int i = 1;i<newheights.length;i++){
if(newheights[i]>=newheights[st.peek()]){
st.push(i);
}else{
while(!st.isEmpty()&&newheights[i]<newheights[st.peek()]){
int mid = st.pop();
int height = newheights[mid];
int weight = i-st.peek()-1;
res = Math.max(res,height*weight);
}
st.push(i);
}
}
return res;
}
}单调栈总结?

单调栈问题入门,找一个元素右边第一个比该元素大的值时考虑使用单调栈,从栈顶到栈底如果是递增趋势(加入的元素是比peek()小的)。找右边第一个元素比该元素值大时为相反情况。需要注意的是,此处我们需要在栈中存放的数值是数组下标。

与上一题相同,一些区别是因为无需考虑数组下标,栈中可以直接存放元素,因为数组之中没有重复元素,所以可以在数组2中寻找完然后再用map对应到数组1中。

这个系列中最简单的一道,循环的部份用取余处理。?

接雨水,横向求取面积,找到左边比当前大的值,右边比当前大的值,height = Math.min(左、右)-mid,weight = 右下标-左下标-1;
?
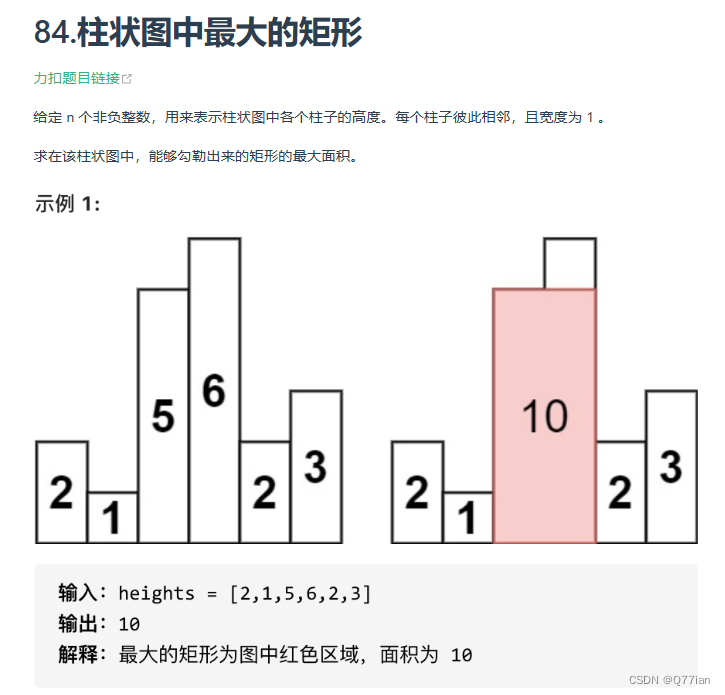
?柱状图中最大的矩形,找到左边比当前小的值和右边比当前小的值,height = mid ,weight就是右下标-左下标-1;
后两道题的难点计算面积并且更新。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!