文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《考虑需求侧响应的电-氢混合储能系统选址定容》

这个标题涉及到考虑了需求侧响应的电-氢混合储能系统的选址和容量确定。

1. 需求侧响应 (Demand Side Response, DSR)：指的是能源系统或网络能够根据需求的变化而灵活调整、响应的能力。在能源管理中，需求侧响应通常指用户或消费者根据能源价格、供应可用性或网络需求变化而调整其能源使用模式的能力。

2. 电-氢混合储能系统：这是一个结合了电力和氢气储能的系统。电-氢混合储能系统通过将电能转化为氢气（通过电解水产生氢气）并将其储存起来，随后可以根据需要将氢气转化回电能（通过燃料电池或其他技术）。这种系统可以用于平衡电力网的负载、储存电能以应对尖峰时段需求等。

3. 选址定容 (Site Selection and Sizing)：指的是确定建立特定设施（如储能系统）的位置和规模。选址包括确定最适合建造储能系统的地理位置，而定容则涉及确定储能系统的适当规模或容量。

综合而言，这个标题意味着在设计一个能够响应需求侧变化的电-氢混合储能系统时，要考虑选址问题（即在哪里建设）以及储能系统的合适容量大小。这可能涉及到考虑不同地点的需求特征、能源供应情况、电力网络状态等因素，并确定最佳的系统规模以满足这些需求。同时，需求侧响应能力也将成为系统设计的关键考量之一。、

摘要：随着分布式电源(distributed generation,DG)在配网接入比例的提高，配网的稳定性受到了剧烈的影响。传统的配电网管理模式很难对多种资源进行协调，因此主动配电网模式逐渐成为电网运营主流。为减小DG接入对主动配电网稳定性的影响，该文建立考虑需求侧响应的电–氢混合(electricity hydrogen hybrid,EHH)储能系统(energy storage system,ESS)双层模型。上层模型以考虑需求侧响应后的最小净负荷波动、最大用户购电成本满意度与用电舒适度为目标，基于电量电价弹性矩阵模型得出最佳分时电价制定策略。下层模型基于上层模型求解出的分时电价策略，以最小EHH-ESS的全生命周期成本(life cycle cost,LCC)、主动配电网电压波动与考虑需求侧响应且接入EHH-ESS后的净负荷波动为目标，通过对EHH-ESS进行最优规划实现其投资经济性、主动配电网负荷稳定性与电压质量的最佳权衡。最后通过扩展的IEEE-33节点验证了该文所提模型的有效性及所采用方法的优越性。同时，通过不同的运营场景对主动配电网的稳定性与EHH-ESS的经济性进行分析，基于NSGA-III算法得到的仿真结果表明：与仅配置EHH-ESS相比，考虑需求侧响应并配置EHH-ESS后，虽然LCC提高了5.16%，但净负荷波动与电压波动分别降低了6.56%与13.33%，验证了在考虑需求侧响应的情况下配置EHH-ESS可最大幅度改善主动配电网的稳定性。?

这段摘要描述了一项研究，主要关注分布式电源（DG）对配电网稳定性的影响，以及通过建立考虑需求侧响应的电-氢混合（EHH）储能系统的双层模型来减小这种影响。

具体来说，摘要中提到的关键点有：

1. DG对配网稳定性的影响：由于分布式电源在配电网中的接入比例增加，传统的配电网管理模式难以有效协调多种资源，从而使得配网的稳定性受到剧烈的影响。

2. 主动配电网模式：为了解决传统管理模式的问题，文章指出主动配电网模式逐渐成为电网运营的主流。主动配电网通过更灵活、智能的方式管理电力流动，以适应分布式电源的变化。

3. 电-氢混合储能系统：为了降低DG接入对主动配电网稳定性的影响，研究建立了考虑需求侧响应的电-氢混合储能系统（EHH-ESS）双层模型。这种储能系统可以通过电-氢转化技术将电能储存为氢气，并在需要时将其转化回电能。

4. 双层模型的目标：上层模型以考虑需求侧响应后的最小净负荷波动、最大用户购电成本满意度与用电舒适度为目标，通过电量电价弹性矩阵模型得出最佳分时电价制定策略。下层模型以最小EHH-ESS的全生命周期成本（LCC）、主动配电网电压波动与考虑需求侧响应且接入EHH-ESS后的净负荷波动为目标，通过最优规划实现投资经济性、负荷稳定性与电压质量的最佳权衡。

5. 验证与分析：通过扩展的IEEE-33节点验证了所提模型的有效性及采用方法的优越性。通过不同的运营场景对主动配电网的稳定性与EHH-ESS的经济性进行分析，得出了在考虑需求侧响应的情况下配置EHH-ESS可以最大幅度改善主动配电网的稳定性的结论。仿真结果表明，虽然全生命周期成本提高了5.16%，但净负荷波动与电压波动分别降低了6.56%与13.33%。

关键词： 需求侧响应;分时电价;电–氢混合储能系统;选址定容;非支配遗传算法;

1. 需求侧响应：指电力系统中的一种管理策略，其中终端用户通过调整其电力需求来响应电网的变化情况。这种响应可以包括在高峰期减少用电，利用低谷期的廉价电力，或者根据电力系统的需求进行灵活的电力调整。在文中，需求侧响应被考虑在建立电-氢混合储能系统模型的上层模型中，以最小化净负荷波动、最大化用户购电成本满意度与用电舒适度为目标。

2. 分时电价：是一种电价制度，其价格根据电力系统的负荷情况和供需平衡的时间变化而变化。在文中，通过电量电价弹性矩阵模型，制定了最佳的分时电价策略，以优化上层模型的目标，考虑了需求侧响应后的最小净负荷波动、最大用户购电成本满意度与用电舒适度。

3. 电–氢混合储能系统：是一种储能系统，结合了电能和氢气的储存技术。该系统通过将电能用于产生氢气，并在需要时将氢气还原为电能。在文中，该系统被用于降低分布式电源接入对主动配电网稳定性的影响。下层模型通过最小化电-氢混合储能系统的全生命周期成本，同时考虑主动配电网电压波动和净负荷波动，来进行系统优化规划。

4. 选址定容：可能是指在建设电-氢混合储能系统时选择合适的地点以及确定储能系统的容量。这可能涉及到对电力系统的结构、负荷分布等因素进行考虑，以最优地安置和调整储能系统的规模。

5. 非支配遗传算法：是一种进化算法的形式，用于解决多目标优化问题。在文中，该算法可能被用于优化下层模型，以实现电-氢混合储能系统的最优规划。非支配遗传算法通常能够找到一组解，其中没有一个解能够被改进而不影响其他目标的解，这有助于找到最优的系统配置。

仿真算例：

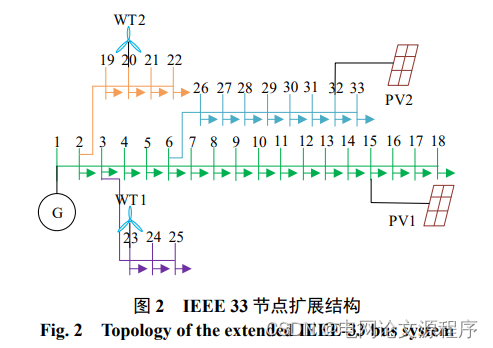
本文在扩展的 IEEE-33 节点上对模型进行验 证。本文分别在节点 15 与 32 接入 2 台装机容量为 1 MW 的风机，节点 23 与 20 接入 2 台装机容量为 0.9 MW 的光伏发电系统。对于 DG 来说，本文仅 考虑其有功功率。无功负荷由主网所提供。主动 配电网主要参数如附录 A表 A1所示，其结构如图 2 所示。EHH-ESS的峰平谷买卖电价[35]如附录 A表 A2 所示，EHH-ESS的参数[36-39]如附录 A表 A3所示。为了验证 NSGA-III 算法的优越性，仿真算例 引入 NSGA-II 与 MOPSO 算法在相同的测试环境 中进行比较。其中，种群数、最大迭代次数与外 部归档集分别设为 50、200 和 50。该小节主要对 上下层模型的 Pareto 前沿、分时电价策略、EHHESS 接入位置与容量、充放电功率、BESS 的 SOC 与 HESS 的 LOH 进行了详细分析，详细过程 请见附录 B。

仿真程序复现思路：请注意，实际实现将取决于仿真环境的具体情况以及您使用的算法。此外，原始文本未提供功率流、优化目标和约束的详细方程和模型，这些信息需要从其他资料中获取。

import numpy as np
import matplotlib.pyplot as plt
from pymoo.algorithms.nsga3 import NSGA3
from pymoo.algorithms.nsga2 import NSGA2
from pymoo.algorithms.mopso import MOPSO
from pymoo.optimize import minimize
from pymoo.util import plotting

# 定义 IEEE-33 节点系统参数
# ...（定义节点位置、网络结构等参数）

# 定义可再生能源（RES）参数
wind_capacity = 1  # 兆瓦
pv_capacity = 0.9  # 兆瓦
wind_nodes = [15, 32]  # 风力涡轮机连接的节点
pv_nodes = [23, 20]  # 光伏系统连接的节点

# 定义 EHH-ESS 参数（见附录 A1、A2、A3）
# ...（包括高峰/低谷电价、EHH-ESS 参数等）

# 定义仿真参数
population_size = 50
max_iterations = 200
archive_size = 50

# 用 NSGA-III 算法模拟系统的函数
def simulate_nsga3():
    algorithm = NSGA3(
        pop_size=population_size,
        n_offsprings=archive_size,
        max_gen=max_iterations,
        # ...（其他特定于算法的参数）
    )

    # ...（实现定义问题、目标、约束等的代码）
    # problem = ...

    # 运行优化
    res = minimize(problem, algorithm, termination=('n_gen', max_iterations), seed=1)

    # 提取并返回结果
    return res

# 用 NSGA-II 算法模拟系统的函数
def simulate_nsga2():
    algorithm = NSGA2(
        pop_size=population_size,
        n_offsprings=archive_size,
        max_gen=max_iterations,
        # ...（其他特定于算法的参数）
    )

    # ...（实现定义问题、目标、约束等的代码）
    # problem = ...

    # 运行优化
    res = minimize(problem, algorithm, termination=('n_gen', max_iterations), seed=1)

    # 提取并返回结果
    return res

# 用 MOPSO 算法模拟系统的函数
def simulate_mopso():
    algorithm = MOPSO(
        pop_size=population_size,
        n_offsprings=archive_size,
        max_gen=max_iterations,
        # ...（其他特定于算法的参数）
    )

    # ...（实现定义问题、目标、约束等的代码）
    # problem = ...

    # 运行优化
    res = minimize(problem, algorithm, termination=('n_gen', max_iterations), seed=1)

    # 提取并返回结果
    return res

# 运行仿真
nsga3_results = simulate_nsga3()
nsga2_results = simulate_nsga2()
mopso_results = simulate_mopso()

# 可视化结果（帕累托前沿、策略等）
plotting.plot_pareto_front(nsga3_results.F, nsga2_results.F, mopso_results.F, labels=["NSGA-III", "NSGA-II", "MOPSO"])
plt.show()

这是一个使用 PyMoo 库的更详细的大纲，PyMoo 是用于多目标优化的 Python 库。实际的实现细节将取决于您的仿真环境、优化问题和所使用的算法。您需要根据您的情况自定义此模板。