【数论】欧拉函数

前置知识：分解质因数

一个数可以被分解为质因数乘积

n =?，其中的pi都是质因数

欧拉函数介绍

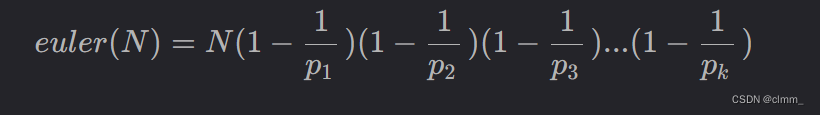
朴素法求欧拉函数

思路：边分解质因数边算欧拉函数

void get_primes() {
	int n; cin >> n;
	int ans = 0;

	int res = n;
	for (int i = 2; i <= n / i; i++) {
		if (n % i == 0) {
			res = res / i * (i - 1);
			while (n % i == 0) n /= i;
		}

	}
	if (n > 1) res = res / n * (n - 1);
	cout << res<<endl;
}

线性筛欧拉函数

在线性筛筛质数的过程中，求出每个数的欧拉函数
可以一次筛的过程中一次性将 [ 1 , N ] 中所有数的欧拉函数都求出来
?

int primes[N], cnt = 0;
int euler[N];
bool st[N];

int get_euler(int n)
{
	euler[1] = 1; // 1的欧拉函数值是1
    
    // 线性筛模板 + 过程中求欧拉函数
    for (int i = 2; i <= n; i++)
    {
        if (!st[i])
        {
            primes[cnt ++] = i;
            euler[i] = i - 1; // (1)式
        }
        for (int j = 0; primes[j] <= n / i; j++)
        {
            st[i *primes[j]] = true;  
            if (i % primes[j] == 0)
            {
                euler[i * primes[j]] = euler[i] * primes[j]; //(2)式
                break;
            }
             euler[i * primes[j]] = euler[i] * (primes[j] - 1);//(3)式
        }
    }
    // 最后，euler数组中存的就是 1 ~ n 每个数的欧拉函数值 
}

文章参考自数论 —— 欧拉函数_euler函数-CSDN博客