代码随想录算法训练营Day16 | 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树

LeetCode 654 最大二叉树

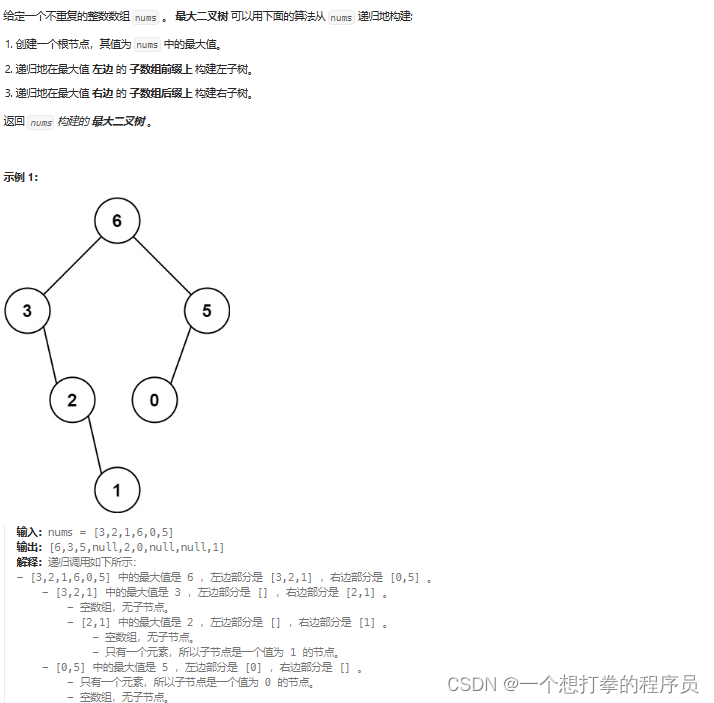
本题思路：我们可以看到每次其实这个找最大值，然后创建节点的过程就是一个二叉树的前序遍历的过程。所以，我们可以递归来完成它。

• 先创找到数组中，最大的值的下标，然后创建根节点
• 然后根据下标，将数组分为，左数组，和右数组
• 然后让根节点的左孩子等于 左数组中的最大值
• 然后让根节点的右孩子等于 右数组中的最大值
• 每一次递归之前，都要重新划分左数组和右数组！

注意：分割数组的时候，要注意区间。左闭右开（自己定义）

为了方便对代码的思路有个好的理解。举个例子演示下：

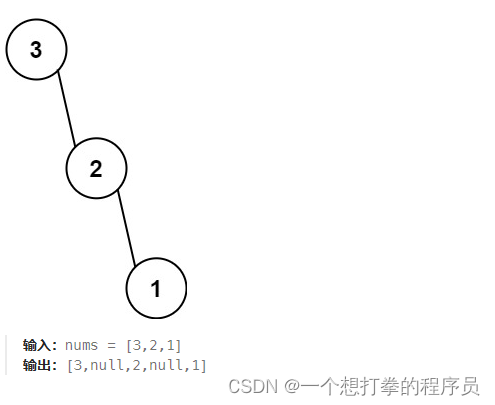
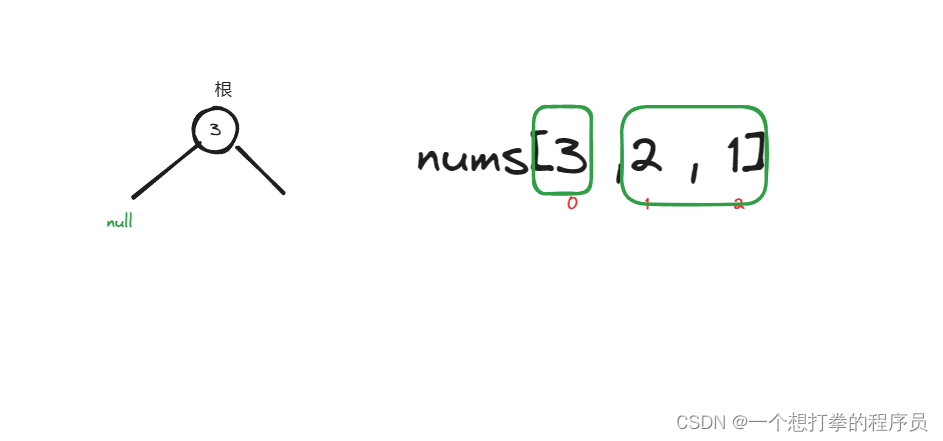
• 首先在 nums 中找到 最大值 3 ，此时下标为 index = 0，创建根节点
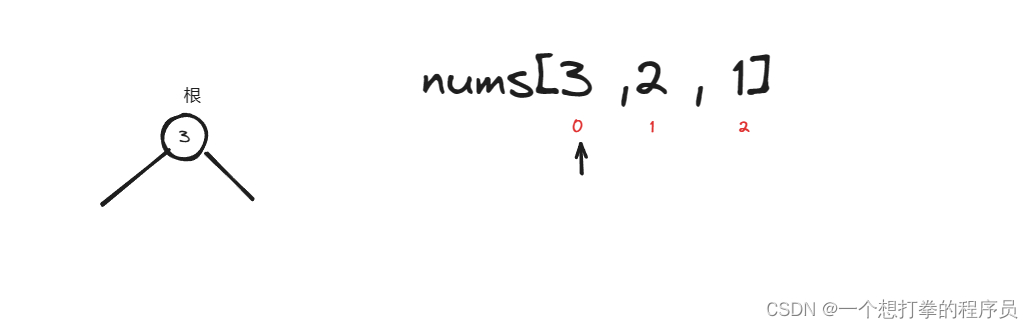
• 然后分割左数组，右数组
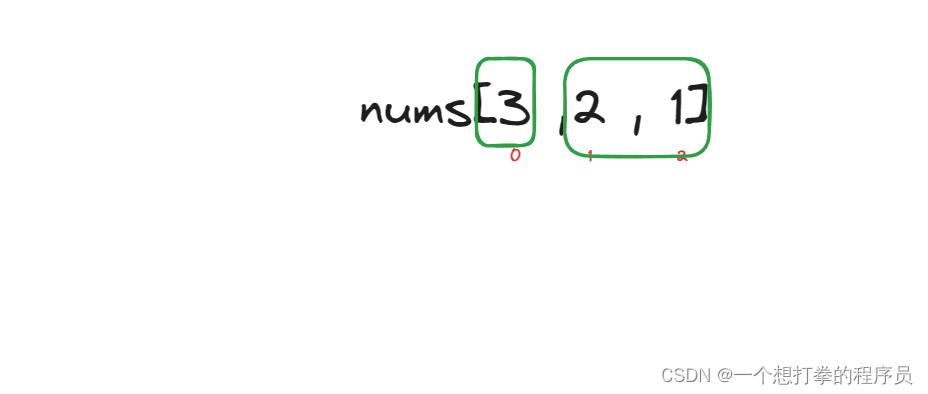
• 再递归进入左数组，进行构造，发现，start 和 end 一样，所以返回 null ，让第一层递归 root.left 接收
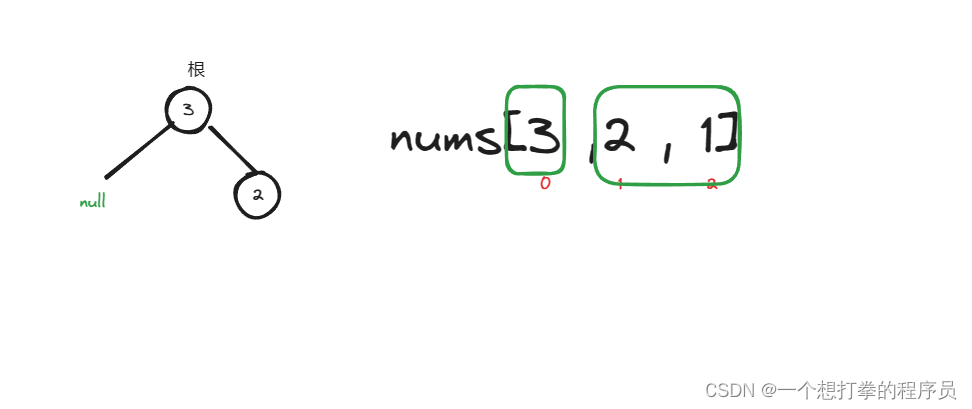
• 再递归进入右数组，找到最大值，并创建节点，由于，start != end，所以会创建，让 root.right 接收
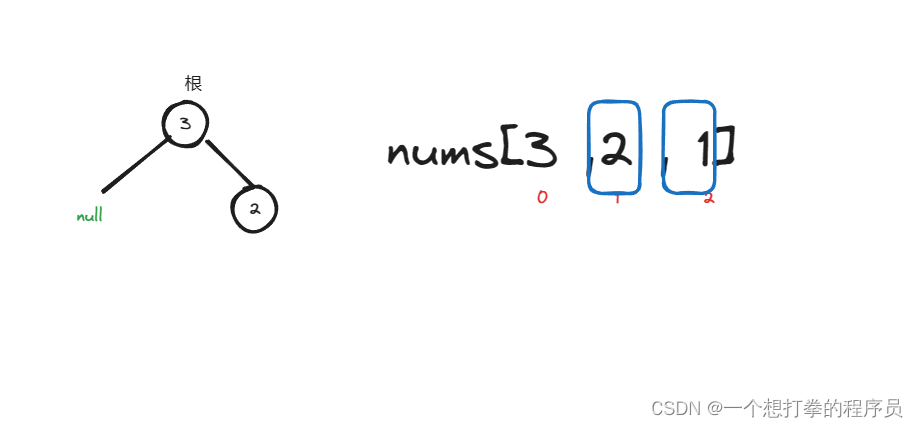
• 此时还要进行分割数组，分为左数组和右数组
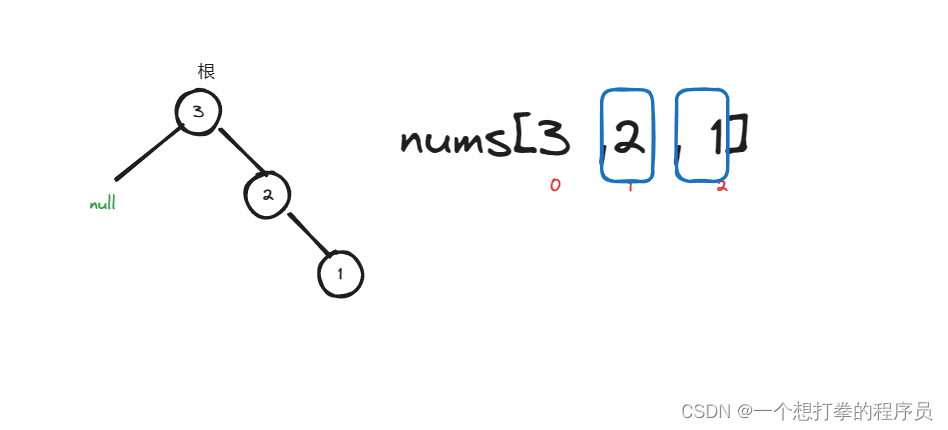
• 然后节点 2 的递归的时候，进入左数组判断返回 null,进入右数组符合条件创建节点。然后给 节点 2 的 right

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return tavel(nums,0,nums.length);
    }
    public TreeNode tavel(int[] nums,int start,int end){
        if(start == end){
            return null;
        }
        int index = findMaxIndex(nums,start,end);
        int rootValue = nums[index];
        TreeNode root = new TreeNode(rootValue);
        if(nums.length == 1){
            return root;
        }
        int leftstart = start;
        int leftend = index;
        int rigthstart = index+1;
        int rightend = end;
        root.left = tavel(nums,leftstart,leftend);
        root.right = tavel(nums,rigthstart,rightend);
        return root;
    }

    public static int findMaxIndex(int[] nums,int start, int end){
        int max = nums[start];
        int index = start;
        for(int i = start + 1; i < end; i++){
            if(nums[i] > max){
                max = nums[i];
                index = i;
            }
        }
        return index;
    }

}

---

LeetCode 617 合并二叉树

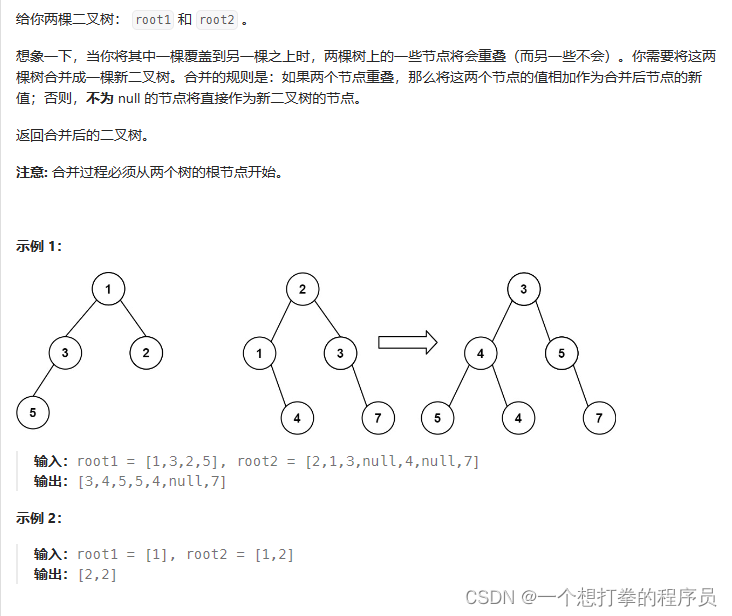
本题思路：利用递归来完成。根据题目的描述，可以得到以下内容。我们用前序遍历来完成

• 如果 root1 和 root2 都为空的情况下，直接返回即可
• 如果 root1 == null，则返回 root2
• 如果 root2 == null，则返回 root1
• 两个不为null，创建节点，val = root1.val + root2.val
• 然后再一次递归，进入左子树，进入右子树

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        // 如果两个都为空，直接返回 null
        if(root1 == null && root2 == null){
            return null;
        }
        // 两个都不为空或者，一个为空
        if(root1 == null){
            return root2; 
        }
        if(root2 == null){
            return root1;
        }
        TreeNode root = new TreeNode(root1.val + root2.val);
        root.left = mergeTrees(root1.left,root2.left);
        root.right = mergeTrees(root1.right,root2.right);
        return root;
    }
}

---

LeetCode 700 二叉搜索树中的搜索

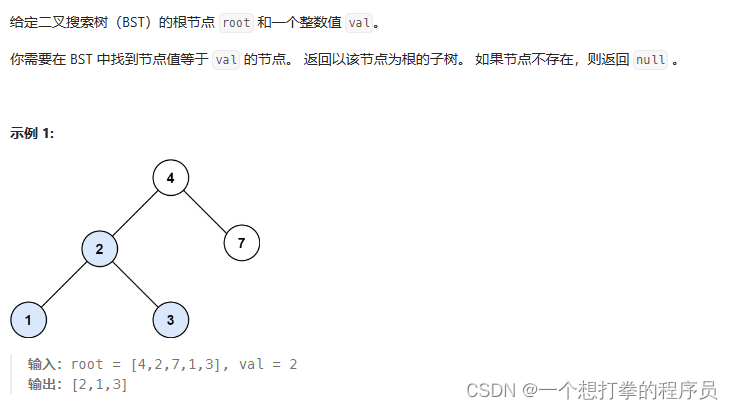
本题思路：使用前序遍历，得到目标节点，返回直接返回即可
为了方便理解，画个图来演示下，这个流程。

• 先遍历根节点，判断是否符合目标值
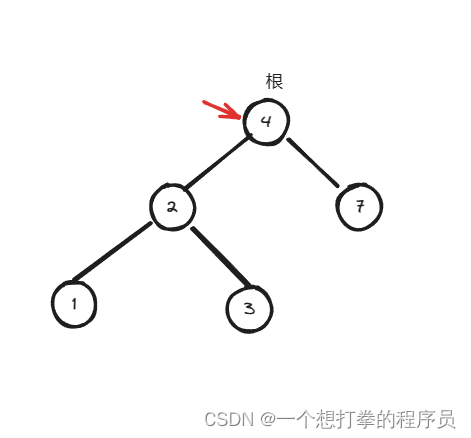
• 发现不符合，就开始递归判断，左树，此时发现符合目标值，于是将这个节点接收
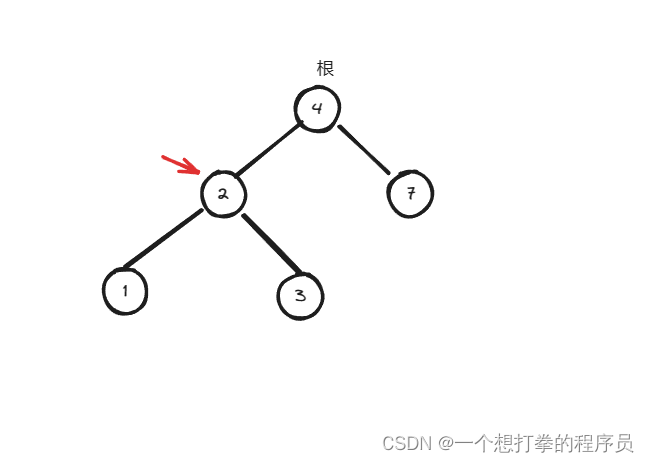
• 然后开始递归判断右树
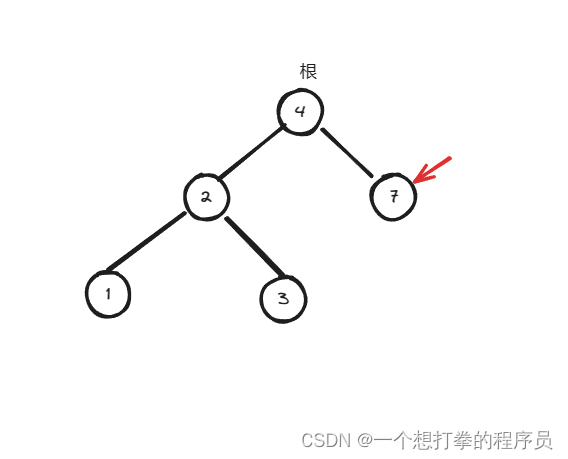
• 进入右树，最终没有符合的就返回 null 接收
• 最后哪个树返回的不是null，就返回哪个节点

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        return preorder(root,val);
    }

    public TreeNode preorder(TreeNode node, int val){
        if(node == null){
            return null;
        }
        if(node.val == val){
            return node;
        }
        TreeNode resleft = preorder(node.left,val);
        TreeNode resright = preorder(node.right,val);
        return resleft == null?resright:resleft;
    }
}

---

LeetCode 98 验证二叉搜索树

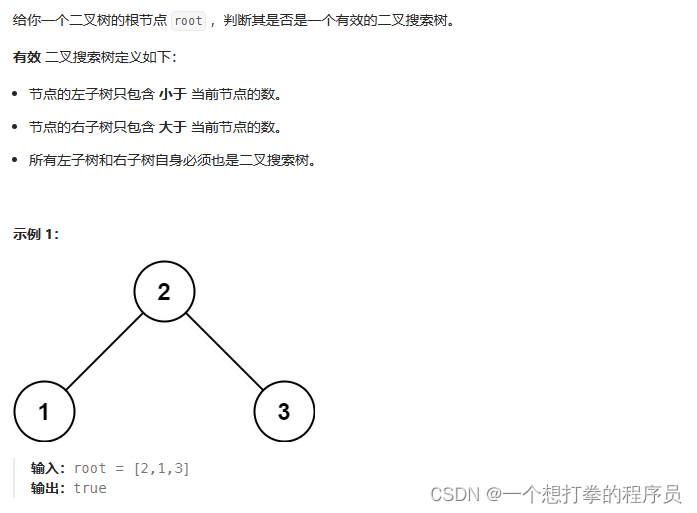
本题思路: 二叉搜索树的中序遍历，是有序单调递增的。所以我的思路是，用中序遍历得到一个列表。然后判断是否是单调递增即可

• 示例1：得到的列表如下
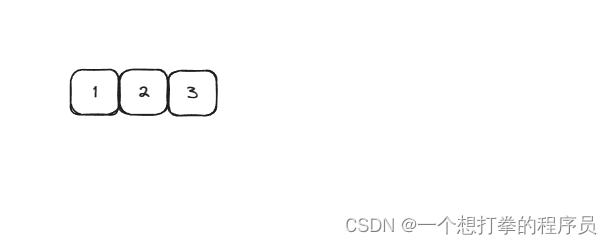
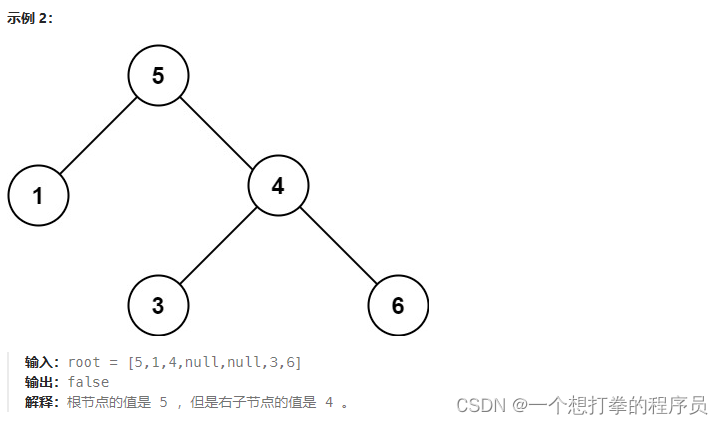
• 示例2: 得到的列表如下
• 可以得到，是否是二叉搜索树，示例1是，示例2不是

class Solution {
    public boolean isValidBST(TreeNode root) {
        List<Integer> list = new ArrayList();
        inorder(root,list);
        for(int i = 1; i < list.size(); i++){
            if(list.get(i-1) >= list.get(i)){
                return false;
            }
        }
        return true;
    }

    public void inorder(TreeNode root,List<Integer> list){
        if(root == null){
            return;
        }
        inorder(root.left,list);
        list.add(root.val);
        inorder(root.right,list);
    }
}