机器学习---clustering
1.?生成不同类型的数据集
导入必要的库:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs代码中导入了NumPy用于数组操作,matplotlib.pyplot用于绘图,KMeans用于聚类算法,
make_blobs用于生成模拟数据集。
plt.figure(figsize=(12, 12))设置了绘图的图形大小为12x12英寸。
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)使用make_blobs函数生成一个包含1500个样本的模拟数据集,其中random_state参数用于控制数
据的随机性。X是包含样本特征的数组,y是对应的样本标签。
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Incorrect Number of Blobs")使用KMeans算法将数据集X聚类为2个簇,并将聚类结果可视化在子图中。subplot(221)表示将整
个图形窗口分为2x2个子图,当前操作的是第1个子图。
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")通过线性变换将原始数据集X变形为X_aniso,然后再使用KMeans算法将变形后的数据集聚类为3
个簇,并将结果可视化在第2个子图中。
X_varied, y_varied = make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")使用make_blobs函数生成一个方差不同的数据集X_varied,并使用KMeans算法将数据集聚类为3
个簇,并将结果可视化在第3个子图中。
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)
plt.subplot(224)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")根据样本标签y的不同值,从原始数据集X中提取不同大小的样本,并使用KMeans算法将提取的数
据集聚类为3个簇,并将结果可视化在第4个子图中。
plt.show()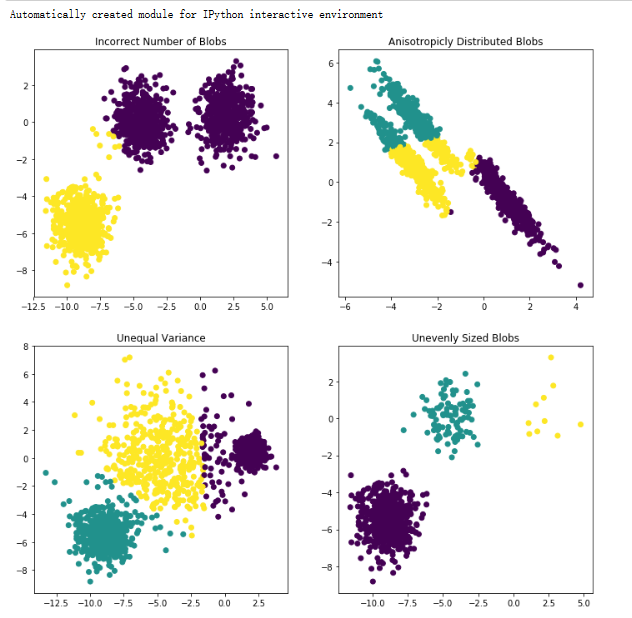
2.?K-means初始化策略
以下是评估的聚类质量度量及其详细解释:
①同质性分数(Homogeneity Score):衡量每个聚类中的样本是否来自同一类别(手写数字)。
同质性分数越高,表示聚类结果中的样本越纯净。
②完整性分数(Completeness Score):衡量同一类别(手写数字)的样本是否被分配到同一个
聚类中。完整性分数越高,表示聚类结果中的类别越完整。
③V度量(V Measure):同质性分数和完整性分数的加权调和平均值,提供了综合的聚类质量度
量。V度量越高,表示聚类结果的质量越好。
④调整兰德指数(Adjusted Rand Index,ARI):衡量真实聚类结果与预测聚类结果之间的相似
性,考虑到了随机匹配的可能性。ARI的取值范围为[-1, 1],值越接近1表示聚类结果与真实结果的
一致性越高。
⑤调整互信息(Adjusted Mutual Information,AMI):衡量真实聚类结果与预测聚类结果之间的
互信息,考虑到了随机匹配的可能性。AMI的取值范围为[0, 1],值越接近1表示聚类结果与真实结
果的一致性越高。
⑥轮廓系数(Silhouette Coefficient):衡量聚类中样本的紧密度和分离度。轮廓系数的取值范围
为[-1, 1],值越接近1表示聚类结果中的样本越紧密且聚类之间的间隔越大,值越接近-1表示聚类结
果存在重叠。
导入所需的库和模块:
from time import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale设置随机种子:
np.random.seed(42)加载手写数字数据集(digits)并进行预处理:
digits = load_digits()
data = scale(digits.data)获取数据集的样本数、特征数和类别数:
n_samples, n_features = data.shape
n_digits = len(np.unique(digits.target))
labels = digits.target设置用于可视化的样本数量:
sample_size = 300打印数据集的相关信息:
print("n_digits: %d, \t n_samples %d, \t n_features %d"
% (n_digits, n_samples, n_features))打印表头和聚类质量度量的标签:
print(82 * '_')
print('init\t\ttime\tinertia\thomo\tcompl\tv-meas\tARI\tAMI\tsilhouette')定义一个函数bench_k_means,用于执行K-Means聚类并输出聚类结果的性能度量:
def bench_k_means(estimator, name, data):
t0 = time()
estimator.fit(data)
print('%-9s\t%.2fs\t%i\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f'
% (name, (time() - t0), estimator.inertia_,
metrics.homogeneity_score(labels, estimator.labels_),
metrics.completeness_score(labels, estimator.labels_),
metrics.v_measure_score(labels, estimator.labels_),
metrics.adjusted_rand_score(labels, estimator.labels_),
metrics.adjusted_mutual_info_score(labels, estimator.labels_),
metrics.silhouette_score(data, estimator.labels_,
metric='euclidean',
sample_size=sample_size)))使用不同的初始化策略对K-Means进行聚类,并调用bench_k_means函数计算聚类性能度量:
bench_k_means(KMeans(init='k-means++', n_clusters=n_digits, n_init=10),
name="k-means++", data=data)
bench_k_means(KMeans(init='random', n_clusters=n_digits, n_init=10),
name="random", data=data)
# 在这种情况下,由于中心点的初始化是确定性的,因此我们只运行一次K-Means算法(n_init=1)
pca = PCA(n_components=n_digits).fit(data)
bench_k_means(KMeans(init=pca.components_, n_clusters=n_digits, n_init=1),
name="PCA-based",
data=data)打印分割线:
print(82 * '_')对降维后的数据进行可视化,并绘制聚类结果的决策边界:
reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init='k-means++', n_clusters=n_digits, n_init=10)
kmeans.fit(reduced_data)
h = .02
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(1)
plt.clf()
plt.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap=plt.cm.Paired,
aspect='auto', origin='lower')
plt.plot(reduced_data[:, 0], reduced_data[:, 1], 'k.', markersize=2)
centroids =K-Means聚类的聚类中心。
```python
kmeans.cluster_centers_绘制聚类中心作为白色十字交叉点:
plt.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='w', zorder=10)设置图形的标题和坐标轴范围,并显示图形:
plt.title('K-means clustering on the digits dataset (PCA-reduced data)\n'
'Centroids are marked with white cross')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()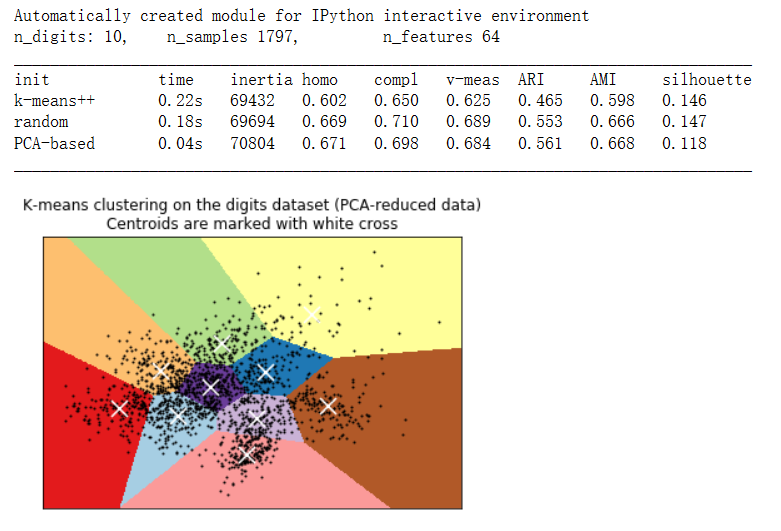
3.?MeanShift算法进行聚类
导入所需的库和模块:
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs
import matplotlib.pyplot as plt
from itertools import cycle生成样本数据:
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)估计带宽(bandwidth)参数:
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)estimate_bandwidth函数用于估计MeanShift算法中的带宽参数。通过该函数,可以根据数据集自
动估计带宽的大小。
使用MeanShift算法进行聚类:
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)创建MeanShift对象,并传入带宽参数。然后,使用聚类算法对数据进行拟合。
获取聚类结果和聚类中心:
labels = ms.labels_
cluster_centers = ms.cluster_centers_通过labels_属性获取每个样本的聚类标签,通过cluster_centers_属性获取聚类中心的坐标。
统计聚类的数量:
labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)使用np.unique函数获取独特的聚类标签,并计算其数量。
打印估计的聚类数量:
print("number of estimated clusters : %d" % n_clusters_)绘制聚类结果的可视化图:
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
my_members = labels == k
cluster_center = cluster_centers[k]
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()创建一个图形窗口,并使用不同颜色的点表示不同的聚类。同时,绘制聚类中心作为圆圈点。最
后,设置图形的标题并显示图形。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!