python实现最小二叉堆---最小堆结构
#来源于MOOC学习以及数据结构与算法分析#
在我们学习最小二叉堆代码实现之前,我们需要去了解一下,什么是最小二叉堆(也有最大二叉堆,也叫最大堆)。
也就是说什么是二叉堆?????
对于这个问题,我们得先知道“优先队列和二叉堆”它们之间的关系。
队列中有一种变体,我们称之为“优先队列”。
根据优先级来决定:优先级最高的在最前面,优先级最低的在最后面。
二叉堆Binary Heap便是用来实现优先队列的数据结构。(二叉堆能够将优先队列的入队和出队的复杂度都保持在O(log n)。
逻辑结构上是为二叉树,但是实际实现是“非嵌套的列表”。
与我们之前说提到过的字典,hash Table ,散列都为ADT 数据结构。
所以它们的方法大多都类似。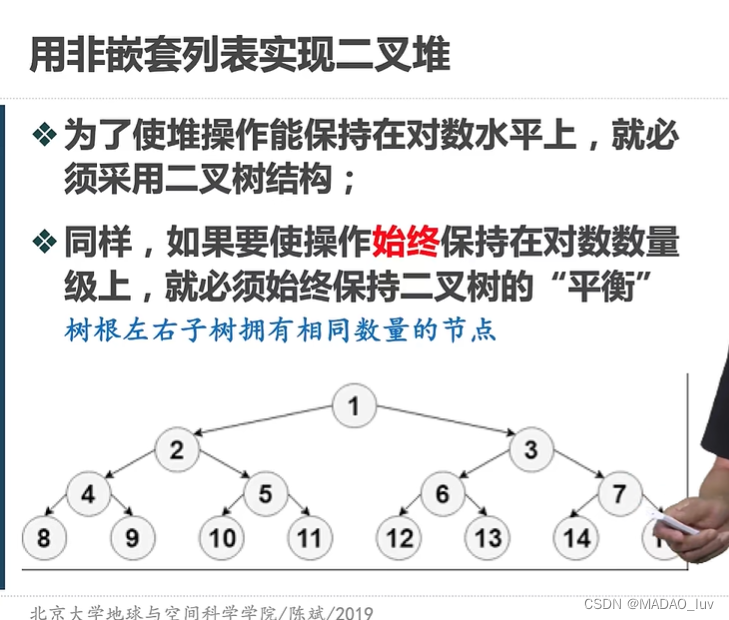
那么,我们开始一步步的最小二叉堆的代码实现吧。
一.二叉堆的初始化
采用一个列表来保持堆数据。表首下标为0的项无用,为了后面代码可以用到简单的整数乘除法,保留它。
#二叉堆的初始化
class BinHeap:
def __init__(self):
self.heaplist = [0]
self.currentSize = 0
"""
二叉堆,也就是我们使用非嵌套的列表,
它的首项一定要是0,占住首位
"""当父节点的下标为K时,那么它的左子节点为2K,而它的右子节点为2K+1.
那么,我们知道一个子节点的下标为N时,它的父节点的位置为(N // 2).
这些操作的实现就是建立在---self.heaplist = [0]
二.二叉堆操作实现:Insert代码
insert(key)方法直接加入到列表末尾,无法保持“堆”次序,虽然对其他路径的次序没有影响,但对于其到根的路径可能破坏次序。
所以我们还需要上浮操作---perup方法
那么我们先来创建辅助方法---perup方法
#perup(上浮)方法
def perUp(self,i):
while i // 2 > 0:
if self.heaplist[i] < self.heaplist[i//2]:
self.heaplist[i],self.heaplist[i//2] = \
self.heaplist[i//2],self.heaplist[i]
i = i // 2
"""
将当前节点与其父节点进行比较,若当前节点小于其父节点
则,当前节点与父节点进行位置交换,进行下一轮的循环。
因为我们创建的是最小堆结构,所以节点越往上,其越小。
"""insert插入操作
#insert方法操作
def insert(self,k):
self.heaplist.append(k)#添加到某尾
self.currentSize = self.currentSize + 1
self.perUp(self.currentSize)#进行上浮操作我们学会了插入节点,那么相同的删除节点,也是轻而易举。
三.二叉堆的delMin()方法实现
delMIn()方法---移走整个堆中最小的key:根节点heaplist[1]
为了保持“完全二叉树”的性质,只用最后一个节点来替代节点。
在这里,我们需要两个辅助方法---percDown 和 minChild
那么,我们先从这两个开始吧。
#percDown 和 minChild 方法
def percDown(self,i):
while (i * 2) <= self.currentSize
mc = self.minChild(i)
if self.heaplist[i] > self.heaplist[mc]:
self.heaplist[i],self.heaplist[mc] = \
self.heaplist[mc],self.heaplist[i]
i = mc
#当节点大于其子节点的时候,两者进行交换,那么它就下沉
#下沉的是我们从末尾移动的节点
def minChild(self,i):
if i * 2 + 1 > self.currentSize:
return i * 2 #唯一子节点
else:
if self.heaplist[i*2] < self.heaplist[i*2+1]:
return i * 2 #选出最小的进行返回
else:
return i * 2 + 1
#返回最小的那个,来维持完全二叉树结构,最小根结构随后就是进行delMIn()操作
#delMin()方法---删除最小值
def delMin(self):
retval = self.heaplist[1] #移走顶项
self.currentSize = self.currentSzie - 1
self.heaplist.pop() #删除尾项
self.percDown(1)
return retval #返回最小值
#因为是最小堆结构,首项一定是最小值三.bulidHeap(lst) : 从无序表生成“堆”。
叶子节点无序下沉
我们用最后节点的父节点开始,因为叶节点无需下沉。
def buildHeap(self,alist):
i = len(alist) // 2
self.currentSize = len(alist)
self.heaplist = [0] + alist[:]
while (i > 0):
self.percDown(i)
i = i - 1
二叉堆的自排序也可以进行排序:堆排序
我会在后续更新出相应的堆排序。
感谢各位的观看,若有任何疑问,欢迎在下面留言
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!