如何信任机器学习模型的预测结果?
机器学习已经在企业中得到了广泛应用。最近在与不同企业的交流中发现,机器学习模型预测结果的可信性得到越来越多的关注。
也就是说,如何确定机器学习模型预测的结果是符合常理的,进而确定所选择的机器学习模型是可信的。
关于这个问题,我将通过两个篇幅向大家介绍机器学习模型的可信性,即机器学习预测结果的解释,以及 MATLAB 如何支持对机器学习模型预测结果的解释,并通过一个例子说明在 MATLAB 中的实现过程。
首先介绍机器学习模型预测结果的解释及 MATLAB 的支持情况。
机器学习模型的可信性
机器学习的目的是在训练数据集中学习到一个最优的模型,并且这个最优模型对未知数据有很好的预测能力(即模型具有很好的泛化能力)。
广泛使用的衡量模型好坏的标准是模型精度,即模型在训练集上的准确度。而在追求模型准确度的过程中,往往会产生过拟合问题,在训练样本不足的情况这个问题尤为严重。模型在训练集上有很好的精度,但是在测试集上精度确很差。因此,仅仅是通过模型的精度进行模型的选择,往往会使得模型的可信度变低,尤其是在过拟合的情况下。
为了避免过拟合,提高机器学习模型的精度,正则化和交叉验证是最常采用的方法。
正则化是遵循结构化风险最小化原则,即减少模型中非零参数的数量(也就是减少变量的个数或者特征的个数),进而从模型结构上降低复杂度。尤其在训练样本不足的情况下,过多的变量或数据特征容易造成模型的过拟合。交叉验证是通过引入验证集提高模型的泛化能力。
交叉验证将训练集进行 k 份(也叫k-fold)的切分,其中 k-1 份用于训练,1 份用于验证。并且不断的交叉选择训练集和验证集,得到 k 个模型训练结果精度,使用 k 个结果的平局值作为最终的模型精度。
不论是正则化的方法,还是交叉验证的方法,选择模型的依据都是比较模型的精度。但是,模型预测结果的合理性或可信性,是决定能否将机器学习模型应用到生产环境下的重要因素。特别是,对于复杂的非线性模型,我们并不清楚为什么能够取得某种预测结果,是那些变量或那些数据特征影响模型的预测结果。这往往使得复杂机器学习模型变成一个黑盒。黑盒模型带来了可信度的问题:
我是否可以相信机器学习模型的预测结果?进而,我是否可以相信训练生成的机器学习模型?
这就引出了今天将要给大家介绍的内容:机器学习模型的可信性。
这里的可信性是指:是否可以对机器学习模型的预测结果给出一个合理的解释,能够定性地呈现出模型输入数据的特征和模型输出的预测结果之间的关系。
通俗的说,我得到的预测结果是受到哪些因素的影响。领域专家往往对研究的领域具有先验知识,当对模型预测结果的解释与先验知识相匹配时,机器学习模型预测结果的可信性就会大大提升,否则就会拒绝预测结果。
如何实现对机器学习模型的预测结果进行解释呢?
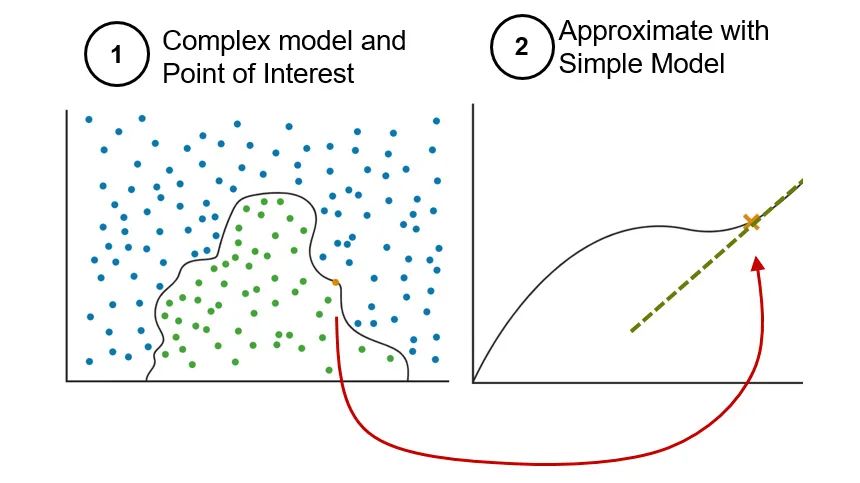
Ribeiro 等人在论文[1]中提出了 LIME(Local Interpretable Model-Agnostic Explanations)。LIME 的目标是:对于一个训练好的机器学习模型,找到一个适合的可解释模型,用于解释机器学习模型的预测结果,也就是定性分析输入数据的特征与预测结果的相关性。这里提到的可解释模型是指模型本身具有自解释性,这中自解释性是由模型结构特性决定的。这类模型主要是指线性模型和决策树模型。
-
线性模型
线性模型 f 可以简单表示为如下的数学表达:
![]()
其中,x1,x2,…,xm?表示输入数据的特征(m 维),ω1,ω2,…,ωm?为模型的系数,系数绝对值的大小表明了输入特征对结果的影响程度。因此,线性模型的可解释性是通过系数的绝对值大小表示的。
-
决策树模型
决策树模型是利用特征对数据进行划分,而选择特征的依据就是特征值能否将数据完全分隔。
如果通过特征值可以将数据完全分隔开(相同标注的数据划分在一起),那么该特征的重要性就会升高;如果通过特征值不能分隔数据(不同标注的数据混在一起),那么这个特征的重要性就会降低。
因此,特征划分数据的能力就体现了特征对结果的影响程度。因此,决策树的可解释性是通过特征的划分能力表示的。如何选择特征进行数据划分,这就要依据于所选择的决策树算法。决策树算法包括:ID3、C4.5 和 CART。关于这些算法,有很多资料可以参考,在这里就不进行说明了。MATLAB 的决策树使用的 CART 算法,决策树既可以用于数据分类也可以用于数据回归。
LIME 正是基于线性模型或决策树模型构建用于解释复杂机器学习模型的可解释模型。对于复杂的机器学习模型,例如支持向量机(SVM),LIME 模型定性说明输入的数据特征对预测结果的影响程度。
LIME 实现对预测结果的解释的方式是:以单个预测数据为基础,通过增加扰动生成合成数据集。合成数据集包含扰动数据以及对应的预测结果。在合成数据集上找到一个可以与复杂的分类模型或回归模型近似的可解释模型,并利用可解释模型来解释原始的机器学习模型的预测结果。
LIME 主要包含三个部分:
-
Local fidelity
Local fidelity 表示 LIME 的局部保真或局部相似性。意味着 LIME 生成的可解释模型必须与复杂机器学习模型在被预测实例附近的预测结果相一致。
-
Interpretable
Interpretable 表示 LIME 的可解释性,这种解释是直接反应输入的数据特征(或变量)对预测结果的影响程度,并且这种解释会重点突出部分数据特征或输入变量而不是全部,因此说 LIME 模型可以给出比较容易理解的解释。
-
Model Agnostic
Model Agnostic 表示 LIME 的模型无关性。LIME 将被解释的原始模型视为一个黑盒(black box),并不关心原始模型的内部细节。LIME 只是通过在输入预测数据的局部范围内生成扰动数据,以及对应的预测结果,进而训练出一个局部近似的可解释模型,该模型与原始机器学习模型的预测结果一致。
上述的三个组成部分也就决定的 LIME 的工作过程。LIME 是对局部数据训练可解释模型。假设有机器学习模型?f,对于一个预测数据?x,x?有 m 维或 m 个特征 :
![]()
(m 表示数据的维度或特征数)
机器学习模型?f?对?x?的预测结果是?p,
![]()
针对预测结果?p,LIME 解释过程如下:
基于概率分布,在?x?的局部范围内随机生成的多个数据样本(称之为合成数据(synthetic data)),由这些数据构成合成数据集?X’?:
![]()
(n 表示数据集中样本的个数,并且每个样本 x_i^'都具有 m 个维度)
对X’中的样本使用机器学习模型?f?进行预测,并生成结果?P’?:
![]()
即:
![]()
由此,产生了一个新的数据集?D = (X’, P’ ),LIME 在新的数据集?D?上训练一个简单的可解释模型?f’(例如,线性模型),并且,该可解释模型对于预测数据?x?的预测结果与机器学习模型?f?的预测结果近似。即:
![]()
因此,通过可解释模型,可以定性的给出数据特征对预测结果的影响程度,即参数?ω1,ω2,…,ωm?的绝对值表示特征对结果的影响程度。
???免费分享一些我整理的人工智能学习资料给大家,整理了很久,非常全面。包括一些人工智能基础入门视频+AI常用框架实战视频、图像识别、OpenCV、NLP、YOLO、机器学习、pytorch、计算机视觉、深度学习与神经网络等视频、课件源码、国内外知名精华资源、AI热门论文等。
下面是部分截图,加我免费领取
目录
一、人工智能免费视频课程和项目
二、人工智能必读书籍
最后,我想说的是,自学人工智能并不是一件难事。只要我们有一个正确的学习方法和学习态度,并且坚持不懈地学习下去,就一定能够掌握这个领域的知识和技术。让我们一起抓住机遇,迎接未来!
上面这份完整版的Python全套学习资料已经上传至CSDN官方,朋友如果需要可以点击链接领取?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!