wy的leetcode刷题记录_Day74

wy的leetcode刷题记录_Day74

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2024-01-10

前言

2696. 删除子串后的字符串最小长度

今天的每日一题是：2696. 删除子串后的字符串最小长度

题目介绍

给你一个仅由 大写 英文字符组成的字符串 s 。

你可以对此字符串执行一些操作，在每一步操作中，你可以从 s 中删除 任一个 “AB” 或 “CD” 子字符串。

通过执行操作，删除所有 “AB” 和 “CD” 子串，返回可获得的最终字符串的 最小 可能长度。

注意，删除子串后，重新连接出的字符串可能会产生新的 “AB” 或 “CD” 子串。

示例 1：
输入：s = “ABFCACDB”
输出：2
解释：你可以执行下述操作：

• 从 “ABFCACDB” 中删除子串 “AB”，得到 s = “FCACDB” 。
• 从 “FCACDB” 中删除子串 “CD”，得到 s = “FCAB” 。
• 从 “FCAB” 中删除子串 “AB”，得到 s = “FC” 。 最终字符串的长度为 2 。 可以证明 2 是可获得的最小长度。

示例 2：
输入：s = “ACBBD”
输出：5
解释：无法执行操作，字符串长度不变。

思路

难得一道简单题：我的想法就是用栈去模拟一遍，很类似后缀表达式的符号栈，只要符合规则就出栈否则就入栈，最后栈中剩余元素个数就是不符合规则的个数。

代码

class Solution {
public:
    int minLength(string s) {
        int n=s.size();
        stack<char> stk;
        for(int i=0;i<n;i++)
        {
            if(stk.empty())
            {
                stk.push(s[i]);         
            }
            else if((s[i]=='B'&&stk.top()=='A')||s[i]=='D'&&stk.top()=='C')
            {
                stk.pop();
            }
            else
                stk.push(s[i]);
        }
        return stk.size();
    }
};

收获

熟练了栈的应用

64. 最小路径和

64. 最小路径和

题目介绍

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

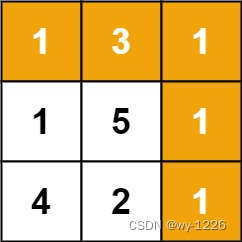
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12

思路

与上一篇文章中的不同路径十分类似，都是二维动态规划，同样的只能向下或者向右遍历因此递推公式没有变， 不过需要计算最小的路径代价，于是我使用一个二维数组来代表path[i][j]来表示到(i,j)所需要的代价，最后返回path[m-1][n-1]

代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> path(m,vector<int>(n));
        path[0][0]=grid[0][0];
        for(int i=1;i<n;i++)
        {
            path[0][i]+=path[0][i-1]+grid[0][i];
        }
        for(int i=1;i<m;i++)
        {
            path[i][0]+=path[i-1][0]+grid[i][0];
        }

        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                path[i][j]=min(path[i-1][j],path[i][j-1])+grid[i][j];
            }
        }
        return path[m-1][n-1];
    }
};

收获

巩固动态规划

63. 不同路径 II

63. 不同路径 II

题目介绍

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

思路

与不同路径I相同的递归方法，不过多了一个条件就是障碍物，当路径上出现障碍物的时候那么表示这条路径不可通立马将path[i][j]置为0即可。

收获

巩固了动态规划