多项式回归

4、多项式回归

4.1、多项式回归基本概念

??升维的目的是为了去解决欠拟合的问题的，也就是为了提高模型的准确率为目的的，因为当维度不够时，说白了就是对于预测结果考虑的因素少的话，肯定不能准确的计算出模型。

??在做升维的时候，最常见的手段就是将已知维度进行相乘（或者自乘）来构建新的维度，如下图所示。普通线性方程，无法拟合规律，必须是多项式，才可以完美拟合曲线规律，图中是二次多项式。

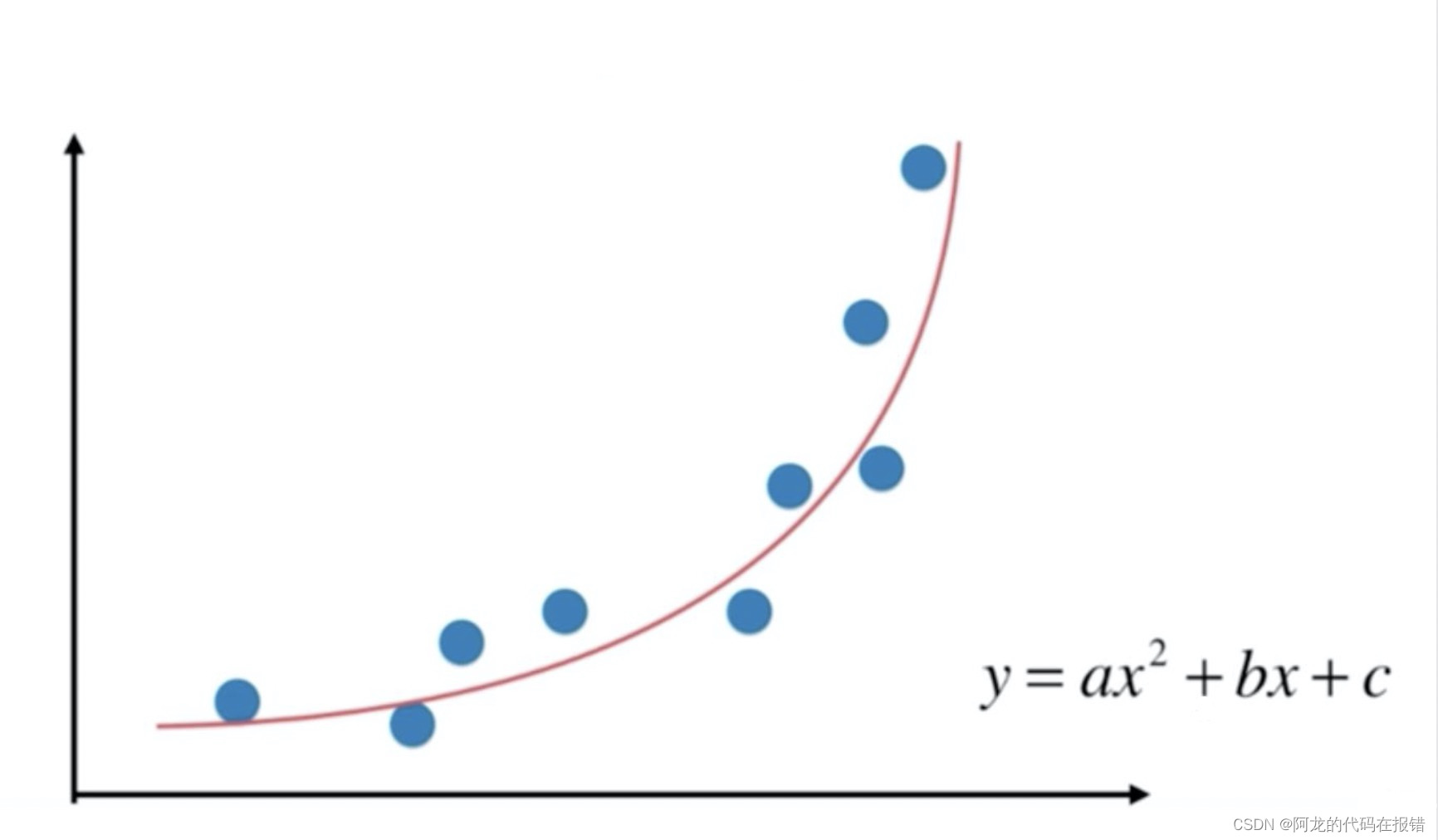
??对于多项式回归来说主要是为了扩展线性回归算法来适应更广泛的数据集，比如我们数据集有两个维度 $x_1、x_2$，那么用多元线性回归公式就是：$\hat{y}=w_0+w_1{x}_1+w_2{x}_2$，当我们使用二阶多项式升维的时候，数据集就从原来的 $x_1、x_2$扩展成了$x_1、x_2、x_1^2、x_2^2、x_1{x}_2$ 。因此多元线性回归就得去多计算三个维度所对应的w值：$\hat{y}=w_0+w_1{x}_1+w_2{x}_2+w_3{x}_1^2+w_4{x}_2^2+w_5{x}_1{x}_2$ 。

??此时拟合出来的方程就是曲线，可以解决一些线性回归的欠拟合问题！

1、普通的线性回归

# 1.创建数据，并进行可视化
X = np.linspace(-1, 11, num=100)
y = (X - 5) ** 2 + 3 * X - 12 + np.random.randn(100)
X = X.reshape(-1, 1)
plt.scatter(X, y, color='red')

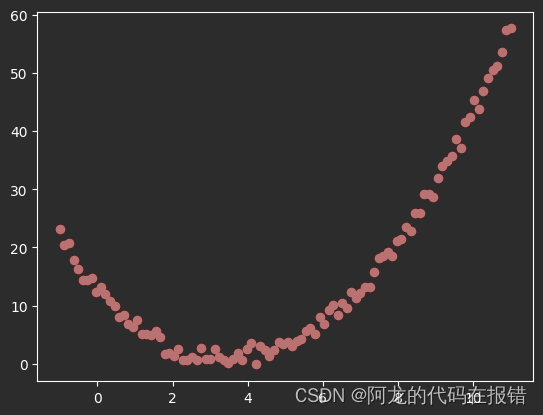
# 使用线性回归进行建模和预测
model1 = LinearRegression()
model1.fit(X, y)
y_pred = model1.predict(X_test)
plt.scatter(X, y, color='red')
plt.plot(X_test, y_pred, color='g')

从下图可以看出线性回归生成图像和真实的红点差距很大

2、多项式回归实战

# 特征升维
X_ = np.c_[X, X ** 2]
model1.fit(X_, y)
print(model1.coef_, model1.intercept_)

# 预测值
X_test_ = np.c_[X_test, X_test ** 2]
y_pred1 = model1.predict(X_test_)
plt.scatter(X,y,color='r')
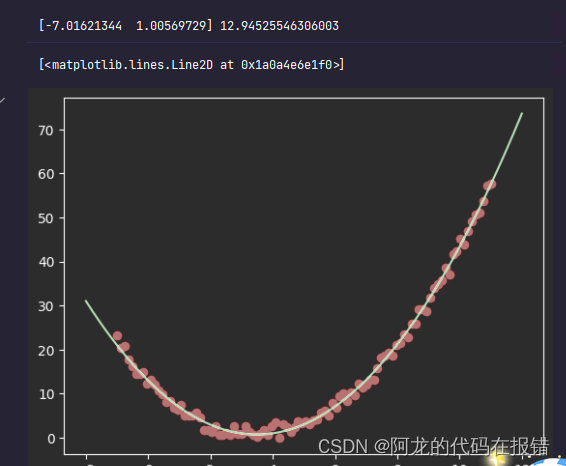
plt.plot(X_test,y_pred1,color='g')

经过多项式回归推导的线性回归的图像和基本和真实的图形重合

3、梯度下降

新导入包

from sklearn.linear_model import SGDRegressor
# 用于构造新特征
from sklearn.preprocessing import PolynomialFeatures

# 1.对数据进行升维
ploy = PolynomialFeatures(interaction_only=False)
x_poly = ploy.fit_transform(X) # 0次幂，1次幂,2次幂
x_poly

X = np.linspace(-1, 11, num=100)
y = (X - 5) ** 2 + 3 * X - 12 + np.random.randn(100)
X = X.reshape(-1, 1)
plt.scatter(X, y, color='red')

model2 = SGDRegressor(eta0=0.001,fit_intercept=False)
model2.fit(x_poly,y)
X_test_poly = ploy.transform(X_test)
y_pred2 = model2.predict(X_test_poly)
plt.scatter(X,y,color='red')
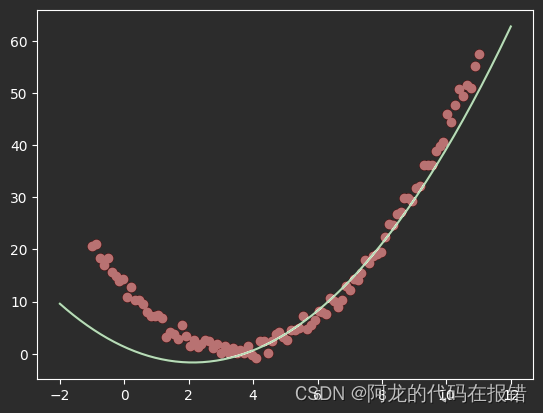
plt.plot(X_test,y_pred2,color='g')
print(model2.coef_,model2.intercept_)

归一化处理

from sklearn.preprocessing import StandardScaler
model3 = SGDRegressor(eta0=0.1,fit_intercept=True)
scaler = StandardScaler()
X_poly_scaler = scaler.fit_transform(x_poly)
model3.fit(X_poly_scaler,y)

x_test_poly = ploy.transform(X_test)
x_test_poly_scaler = scaler.transform(x_test_poly)

y_pred3 = model3.predict(x_test_poly_scaler)
plt.scatter(X,y,color ='red')
plt.plot(X_test,y_pred3,color='g')
print(model3.coef_,model3.intercept_)

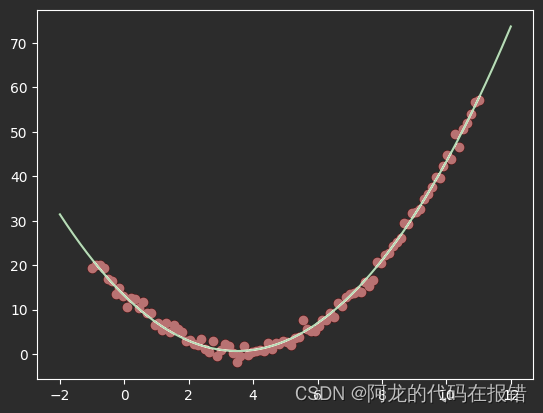
经过归一化处理和参数调优后预测值和真实点基本上重合

坚持学习，整理复盘