C++ OJ题测试—排序算法效率

2023-12-19 22:47:13

OJ链接

一、直接插入排序

二、希尔排序

OJ链接

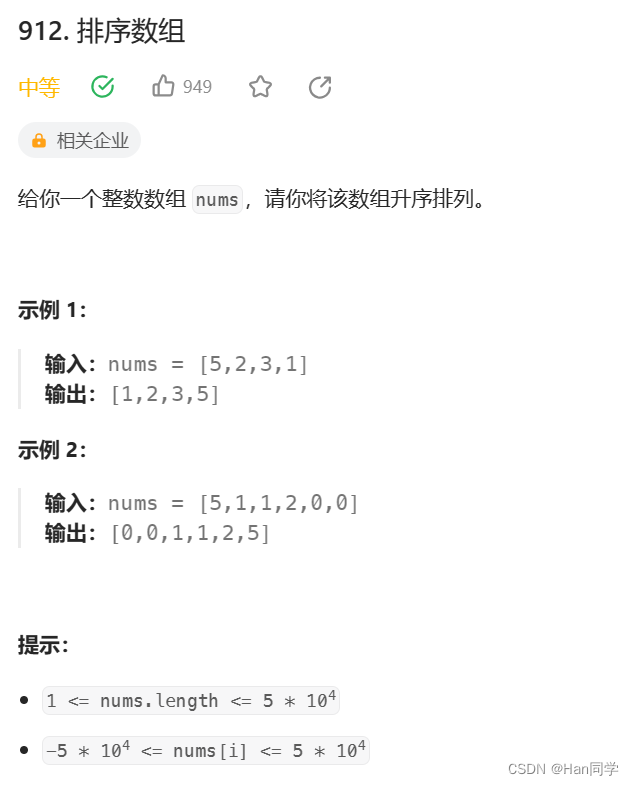一、直接插入排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for(int i=0;i<nums.size()-1;i++)
        {
            int end=i;
            int tmp=nums[i+1];
            while(end>=0)
            {
                if(nums[end]>tmp)
                {
                    nums[end+1]=nums[end];
                    --end;
                }
                else
                    break;
            }
            nums[end+1]=tmp;
        }
        return nums;
    }
};

二、希尔排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int gap=nums.size();
        while(gap>1){
            gap=gap/3+1;
            for(int i=0;i<nums.size()-gap;i++){
                int end=i;
                int tmp=nums[end+gap];
                while(end>=0){
                    if(nums[end]>tmp){
                        nums[end+gap]=nums[end];
                        end-=gap;
                    }
                    else
                        break;
                }
                nums[end+gap]=tmp;
            }
        }
        return nums;
    }
};

三、直接选择排序

常规：?

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int i,j,minIndex,temp;
        for(i=0;i<nums.size()-1;i++){
            minIndex=i;
            for(j=i+1;j<nums.size();j++){
                if(nums[j]<nums[minIndex])
                    minIndex=j;
            }
            temp=nums[i];
            nums[i]=nums[minIndex];
            nums[minIndex]=temp;
        }
        return nums;
    }
};

?第二种：

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int begin=0,end=nums.size()-1;
        while(begin<end){
            int maxi=begin,mini=begin;
            for(int i=begin;i<=end;i++){
                if(nums[i]>nums[maxi])
                    maxi=i;
                if(nums[i]<nums[mini])
                    mini=i;
            }
            swap(nums[begin],nums[mini]);
            if(begin==maxi)
                maxi=mini;
            swap(nums[maxi],nums[end]);
            ++begin;
            --end;
        }
        return nums;
    }
};

四、堆排序

class Solution {
public:
    void AdjustDown(vector<int>& a,int n,int parent)
    {
        int child=parent*2+1;
        while(child<n){
            if(child+1<n&&a[child+1]>a[child])
                ++child;
            if(a[child]>a[parent]){
                swap(a[child],a[parent]);
                parent=child;
                child=parent*2+1;
            }
            else{
                break;
            }
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        for(int i=(nums.size()-1-1);i>=0;i--){
            AdjustDown(nums,nums.size(),i);
        }
        int end=nums.size()-1;
        while(end>0){
            swap(nums[0],nums[end]);
            AdjustDown(nums,end,0);
            --end;
        }
        return nums;
    }
};

五、冒泡排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for (int j = 0; j < nums.size(); ++j){
            bool exchange = false;
            for (int i = 1; i < nums.size() - j; i++)
            {
                if (nums[i - 1] > nums[i])
                {
                    int tmp = nums[i];
                    nums[i] = nums[i - 1];
                    nums[i - 1] = tmp;
    
                    exchange = true;
                }
            }
    
            if (exchange == false)
            {
                break;
            }
        }
        return nums;
    }
};

六、快速排序

常规：

class Solution {
public:
    int GetMidIndex(vector<int>& a, int left, int right)
    {
        int mid = (left + right) >> 1;
        if (a[left] < a[mid])
        {
            if (a[mid] < a[right])
            {
                return mid;
            }
            else if (a[left] < a[right])
            {
                return right;
            }
            else
            {
                return left;
            }
        }
        else // a[left] > a[mid]
        {
            if (a[mid] > a[right])
            {
                return mid;
            }
            else if (a[left] > a[right])
            {
                return right;
            }
            else
            {
                return left;
            }
        }
    }
    void QuickSort(vector<int>& a, int begin, int end)
    {
        if (begin >= end)
            return;
    
        int keyi = PartSort3(a, begin, end);
        QuickSort(a, begin, keyi - 1);
        QuickSort(a, keyi + 1, end);
    }
    
    int PartSort3(vector<int>& a, int left, int right)
    {
        int midi = GetMidIndex(a, left, right);
        swap(a[left], a[midi]);
    
        int prev = left;
        int cur = left + 1;
        int keyi = left;
        while (cur <= right){
            if (a[cur] < a[keyi] && ++prev != cur){
                swap(a[prev], a[cur]);
            }
            ++cur;
        }
       swap(a[prev], a[keyi]);
        keyi = prev;
        return keyi;
    }
    vector<int> sortArray(vector<int>& nums) {
        QuickSort(nums,0,nums.size()-1);
        return nums;
    }
};

三路划分优化效率

class Solution {
public:
    int GetMidIndex(vector<int>& a, int left, int right)
    {
        int mid = left + (rand()%(right-left));
        if (a[left] < a[mid])
        {
            if (a[mid] < a[right])
            {
                return mid;
            }
            else if (a[left] < a[right])
            {
                return right;
            }
            else
            {
                return left;
            }
        }
        else // a[left] > a[mid]
        {
            if (a[mid] > a[right])
            {
                return mid;
            }
            else if (a[left] > a[right])
            {
                return right;
            }
            else
            {
                return left;
            }
        }
    }

    void QuickSort(vector<int>& a, int begin, int end)
    {
        if (begin >= end)
            return;

        int left = begin;
        int right = end;
        int cur = left + 1;

        int midi = GetMidIndex(a, left, right);
        swap(a[left], a[midi]);
        int key = a[left];

        while (cur <= right)
        {
            if (a[cur] < key)
            {
                swap(a[left], a[cur]);
                ++left;
                ++cur;
            }
            else if (a[cur] > key)
            {
                swap(a[right], a[cur]);
                --right;
            }
            else
            {
                ++cur;
            }
        }

        QuickSort(a, begin, left - 1);
        QuickSort(a, right + 1, end);
    }

    vector<int> sortArray(vector<int>& nums)
    {
        srand(time(0));

        QuickSort(nums, 0, nums.size() - 1);

        return nums;
    }
};

?GetMidIndex：这个方法用于在快速排序的过程中选择一个"基准"元素。它首先随机选择一个索引mid，然后比较数组a在left、mid和right这三个位置的元素，返回这三个元素中的中位数的索引。这种方式可以有效地避免在处理近乎有序的数组时，快速排序退化为O(n^2)的情况。
QuickSort：这是快速排序的主要方法。它首先调用GetMidIndex方法获取基准元素的索引，然后将基准元素与数组的第一个元素交换位置，接着遍历数组，将小于基准的元素放到左边，大于基准的元素放到右边，等于基准的元素不动。最后，递归地对基准元素左边和右边的子数组进行同样的操作。?
sortArray：这是对外的接口方法，它首先初始化随机数种子，然后调用QuickSort方法对输入的数组nums进行排序，最后返回排序后的数组。

这段代码的主要优点是它使用了随机化的快速排序算法，可以在平均情况下达到O(n log n)的时间复杂度，而且它的空间复杂度为O(log n)，因为它只需要递归调用栈的空间。

七、归并排序

class Solution {
public:
    void InsertSort(vector<int>& a, int begin, int end)
    {
        for(int i=begin+1; i<=end; i++)
        {
            int tmp=a[i];
            int j=i;
            while(j>begin && a[j-1]>tmp){
                a[j]=a[j-1];
                j--;
            }
            a[j]=tmp;
        }
    }
    void _MergeSort(vector<int>& a,int begin,int end,vector<int>& tmp)
    {
        if (begin >= end) {
            return;
        }
        if (end - begin + 1 < 10){
	    	InsertSort(a, begin, end);
	    	return;
	    }
        int mid=(begin+end)/2;
        _MergeSort(a,begin,mid,tmp);
        _MergeSort(a,mid+1,end,tmp);
        int begin1=begin,end1=mid;
        int begin2=mid+1,end2=end;
        int i=begin;
        while(begin1<=end1&&begin2<=end2)
        {
            if(a[begin1]<a[begin2])
                tmp[i++]=a[begin1++];
            else
                tmp[i++]=a[begin2++];
        }
        while(begin1<=end1)
            tmp[i++]=a[begin1++];
        while(begin2<=end2)
            tmp[i++]=a[begin2++];
        for (i = begin; i <= end; i++)
        {
            a[i] = tmp[i];
        }
    }
    vector<int> sortArray(vector<int>& nums)
    {
         vector<int> tmp(nums.size());
        _MergeSort(nums,0,nums.size()-1,tmp);
        return nums;
    }
};

八、计数排序

class Solution {
public:
    
    vector<int> sortArray(vector<int>& nums)
    {
        // 找到数组中的最大值和最小值
        int minVal = INT_MAX, maxVal = INT_MIN;
        for (int num : nums) {
            minVal = min(minVal, num);
            maxVal = max(maxVal, num);
        }
        
        // 统计每个元素出现的次数
        vector<int> count(maxVal - minVal + 1, 0);
        for (int num : nums) {
            count[num - minVal]++;
        }
        
        // 根据统计结果重新构造排序后的数组
        vector<int> sortedArray;
        for (int i = 0; i < count.size(); i++) {
            for (int j = 0; j < count[i]; j++) {
                sortedArray.push_back(i + minVal);
            }
        }
        
        return sortedArray;
    }
};

当我们使用计数排序算法时，我们首先需要找到待排序数组中的最大值和最小值。这是为了确定计数数组的大小，以及后续构造排序后的数组时的索引范围。
接下来，我们创建一个计数数组?count，其大小为?maxVal - minVal + 1，其中?maxVal?是数组中的最大值，minVal?是数组中的最小值。计数数组用于统计每个元素出现的次数。
然后，我们遍历待排序数组?nums，对于每个元素?num，我们将其在计数数组中对应的位置的值加1，表示该元素出现了一次。
接着，我们根据统计结果重新构造排序后的数组?sortedArray。我们从计数数组的第一个位置开始遍历，对于每个计数数组的索引?i，我们将其对应的值?count[i]?表示的元素值（即?i + minVal）按照出现次数依次添加到?sortedArray?中。
最后，我们返回排序后的数组?sortedArray。

计数排序算法的时间复杂度为 O(n+k)，其中 n 是待排序数组的长度，k 是待排序元素的范围。由于计数排序是一种稳定的排序算法，它可以在线性时间内完成排序。

文章来源:https://blog.csdn.net/m0_73800602/article/details/135032247
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！