【电机控制】PMSM无感foc控制(七)滑模观测器的应用
0. 前言
????????前面我们讲解了foc的整个流程框图,如图0-1所示,其中的坐标变换、PID控制以及SVPWM都已讲解完毕,接下来会用通俗易懂的方式(不会涉及到特别复杂难以理解的公式)来讲解滑模观测器是如何得到的反电动势,从而提取出转子位置及转速。

图0-1 FOC双环控制系统框图
1. 滑模观测器
??????? 建议大家先看一下滑模观测器的大致概念,不用完全理解,但是在后面看完滑模观测器在电机控制中的应用后能将后面的内容与前面的概念一一对应起来。
1.1 滑模观测器的概念
??????? 通俗点讲滑模观测器(Sliding Mode Observer,SMO)就是一种在控制工程中用来估计系统未知变量的观测技术。它的基本思想是利用系统的输入和输出信号来估计出那些无法直接测量的状态或参数。
??????? 比如你有一个控制系统,比如一个电机,你想知道它当前的速度或者位置,但这些信息可能很难直接获取。这时,滑模观测器就能派上用场。它通过构造一个虚拟的“滑动面”,并让系统在这个面上以一种特定的方式运动(也就是“滑动”),这样就可以从系统的输入和输出数据推算出电机的速度和位置等信息。
具体来说,滑模观测器的应用可以分为以下几个步骤:
定义滑动面:首先,我们需要找到一个能反映系统状态的函数,这个函数通常被称为滑动面函数。当系统的实际状态满足这个函数时,我们说系统处于“滑动模态”。
设计控制函数:接下来,我们要设计一个控制器(控制函数),使得系统能够尽可能快地到达滑动面,并且一旦到达就始终保持在滑动面上。这通常需要设计一个开关函数,根据系统的当前状态调整控制器的输出。
估计未知变量:最后,我们在滑动面上观察系统的动态行为。由于在滑动面上系统的行为与一些不可观测的参数无关,因此可以通过分析滑动面上的系统行为来估计这些未知变量。
????????通俗来讲,滑模观测器就像是一个侦探,它通过观察系统的外在表现(输入和输出),然后运用一些特殊的技巧(滑动模态),来推测出系统内部的一些秘密(未知状态或参数)。这种观测方法具有鲁棒性好、对噪声不敏感的特点,所以在许多工程应用中都得到了广泛的应用。
??????? 这个概念可能有点模糊,大家结合后面的实例就能理解了。
1.2 滑模观测器在观测什么
??????? 首先既然它叫滑模观测器,那我们到底是想通过它观测什么?
????????答案就是观测了α和β轴的反电动势。
??????? 为什么要观测α和β轴的反电动势?
????????因为我们要知道转子的角度和速度,而这两个变量刚好包含在反电动势中。
??????? 根据电机的数学模型(此处是针对表贴式PMSM建立的电压方程,Ld = Lq)可知,电机在静止坐标系α-β中的电压方程(式1.1):

????????其中α和β轴的反电动势方程(式1.2):

????????
????????Uα、Uβ为定子在α和β轴上的电压;
????????Rs为定子电阻;
??????? Ls为定子电感;
????????Iα、Iβ为定子在α和β轴上的电流;
????????p代表微分;
????????eα、eβ为α和β轴的反电动势;
??????? ωr为转子电角速度;
????????ψf为永磁体磁链;
????????θr为定子角度;
????????可见α和β轴的反电动势包含了转子转速以及角度信息,所以我们得想办法得到反电动势,并从中提取出需要的信息。
????????我们整理上式可以得出电流方程(式1.3):
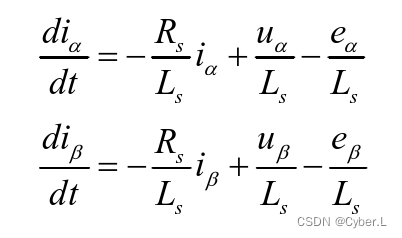
??????? (这个方程很重要,滑模观测器的应用就是基于这个方程来的。)
????????通过式1.3我们发现通过αβ轴的电流微分、电流的大小、电压大小、定子电阻、定子电感我们就能直接计算出αβ轴的反电动势。
????????那既然αβ轴的反电动势能直接能计算出来是不是就不需要通过滑模去观测了?
??????? 答案是可以的,在电机控制中确实可以直接通过αβ轴的电流方程来求解反电动势。这种方法被称为“解析法”,它基于电磁学原理和电机模型。
????????但是在实际应用中,电机参数可能因为温度、老化等原因发生变化,或者存在测量误差等干扰因素。解析法在这种情况下可能会导致计算结果不准确,而滑模观测器则能更好地抵抗这些扰动。
1.3 滑模观测器的大致原理
??????? 注意本节只是引导大家理解滑模观测器估算反电动势的大致原理,有些说法并不严谨,是为了大家先去理解从而引出后面的内容。
??????? 之前我们说过式1.3这个方程很重要,滑模观测器的应用就是基于这个方程来的,那具体怎么应用的呢?
????????我们先看一下这两组方程,实际电流方程与估算电流方程如图1-1:
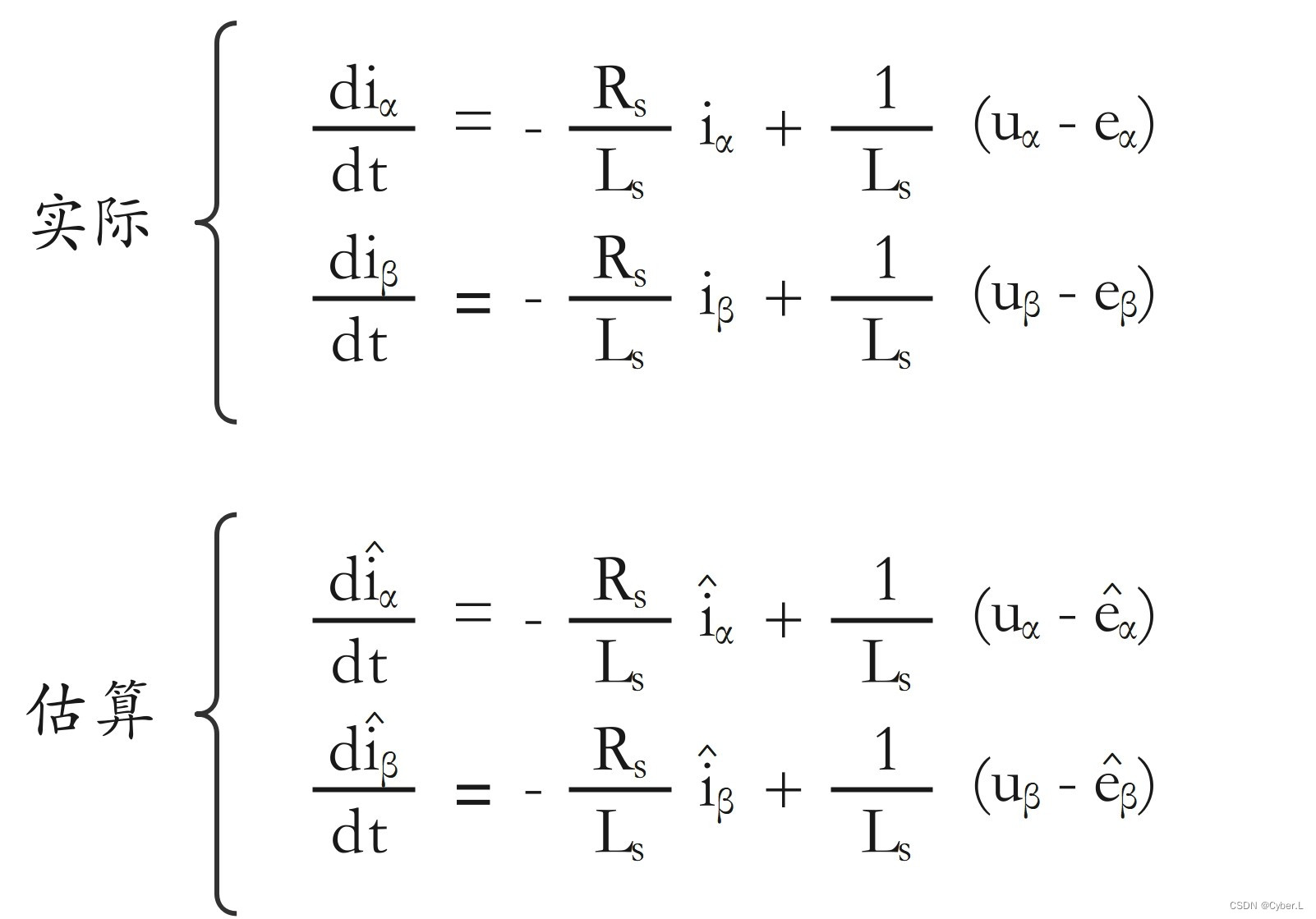
图1-1 实际电流方程与估算电流方程
????????上面一组方程代表实际电流方程,下面一组代表估算的电流方程。
??????? 两个方程组趋于一致时估算的反电动势是不是就等效于实际的反电动势,那么怎么判断估算的电流方程是否和实际的电流方程趋于一致呢?
??????? 当实际的αβ轴电流随时间的变化率、实际的αβ轴电流、实际的αβ轴反电动势与估算的αβ轴电流随时间的变化率、估算的αβ轴电流、估算的αβ轴反电动势一致时就趋于一致了。
??????? 我们用估算电流减去实际电流,得到差值用下面方程组表示,如图1-2:

?图1-2 估算电流与实际电流的差值
????????也就是说当 时,我们估算的反电动势的值就与实际值一致了。
时,我们估算的反电动势的值就与实际值一致了。
??????? 那我们要怎样才能达到这个 状态呢?
状态呢?
??????? 观察图1-2差值的方程式后不难发现,只要我们根据电流的差值,不断调整估算的αβ轴反电动势就能达到这个状态。
????????这么描述有点不好理解,举两个例子如下:

????????控制框图如图1-3所示:

图1-3 滑模观测器控制框图
??????? 就是我们不断地调整α轴的反电动势,使得实际的α轴电流与预估的α轴电流一直保持一致,这时候我们给出的预估的反电动势就是实际的反电动势。

2. 滑模观测器的应用
??????? 本节讲解的滑模观测器应用的步骤与1.1里面的描述一致。
2.1 定义滑动面
????????首先我们要定义一个滑动面,然后根据滑动面的状态去设计控制函数;很明显上一节我们是根据预估的αβ轴电流与实际的αβ轴电流去调整预估的反电动势大小的,所以我们选取滑动面函数S(x)为:
![]()
????????根据上式我们可以知道滑动面函数对时间t的导数为:

???????? 通过这两个函数我们就可以引出滑动模态的存在条件为:
![]()
????????是不是有点难以理解上面的式子,用通俗易懂的文字描述一下:
????????我们可以将系统状态空间看作一个二维平面,其中横坐标表示系统的实际状态,纵坐标表示滑动面函数 S 的值。滑动面则是一条垂直于横坐标的直线,即 S=0。假设初始时,系统在某个点 (x0,S0) 处,而我们希望它能尽快到达滑动面并保持在那里。
??????? 首先,我们需要设计一个控制器,使得当系统不在滑动面上S >0时,S˙<0。这意味着在控制作用下,系统状态沿着斜率为负的方向变化,也就是朝向滑动面方向运动。
????????随着控制输入的作用,系统开始沿着滑动面函数减小的方向移动,直到最终达到滑动面。此时,系统的状态满足 S=0,也就是说,系统处于滑动面上。
????????一旦系统到达滑动面,控制器会确保 S˙=0 或者 S?S˙=0,这意味着系统不会离开滑动面,而是沿着滑动面稳定地滑行。
??????? 那么我们又该如何设计控制器呢?
????????通过上一节的图1-2不难看出我们只需要将预估的反电动势那一项设计成与S相关的函数就能达到上述效果。
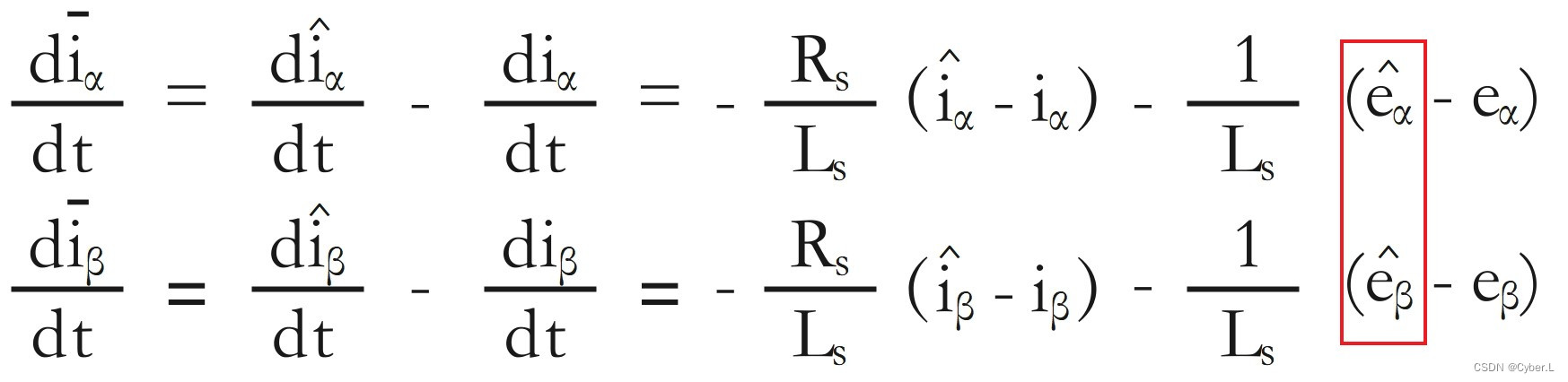
2.2 设计控制函数
??????? 我们把图1-2中的预估的反电动势用u(x)替换掉:

???????? u(x)的设计需要满足切换面到达条件的要求,使得切换面上的点都是止点, 从而形成滑动模态区。
????????滑模控制中u(x)选择形式有很多种,无论哪种形式,都要满足到达条件,既要考虑到其实现难易程度,也要防止过大,以免出现饱和失控现象,本章我们就只挑常值切换控制来讲解。
????????常值切换控制:![]() ,u0是代求常数,要确定u就是确定u0;
,u0是代求常数,要确定u就是确定u0;
??????? sgn(S(x))为:? 
??????? 那么现在的问题就是如何确定u0?
????????首先我们回顾一下上一节的电流方程把预估的反电动势用常值切换控制函数替换,u0取l1得:

??????? 用 电流滑模观测方程 - 电流状态方程 得:
????????要保证滑模到达条件![]() 成立,l1的取值尤为重要,下面分析一下的l1取值范围,由前面得结论
成立,l1的取值尤为重要,下面分析一下的l1取值范围,由前面得结论![]() 可得:
可得:

????????同理得:
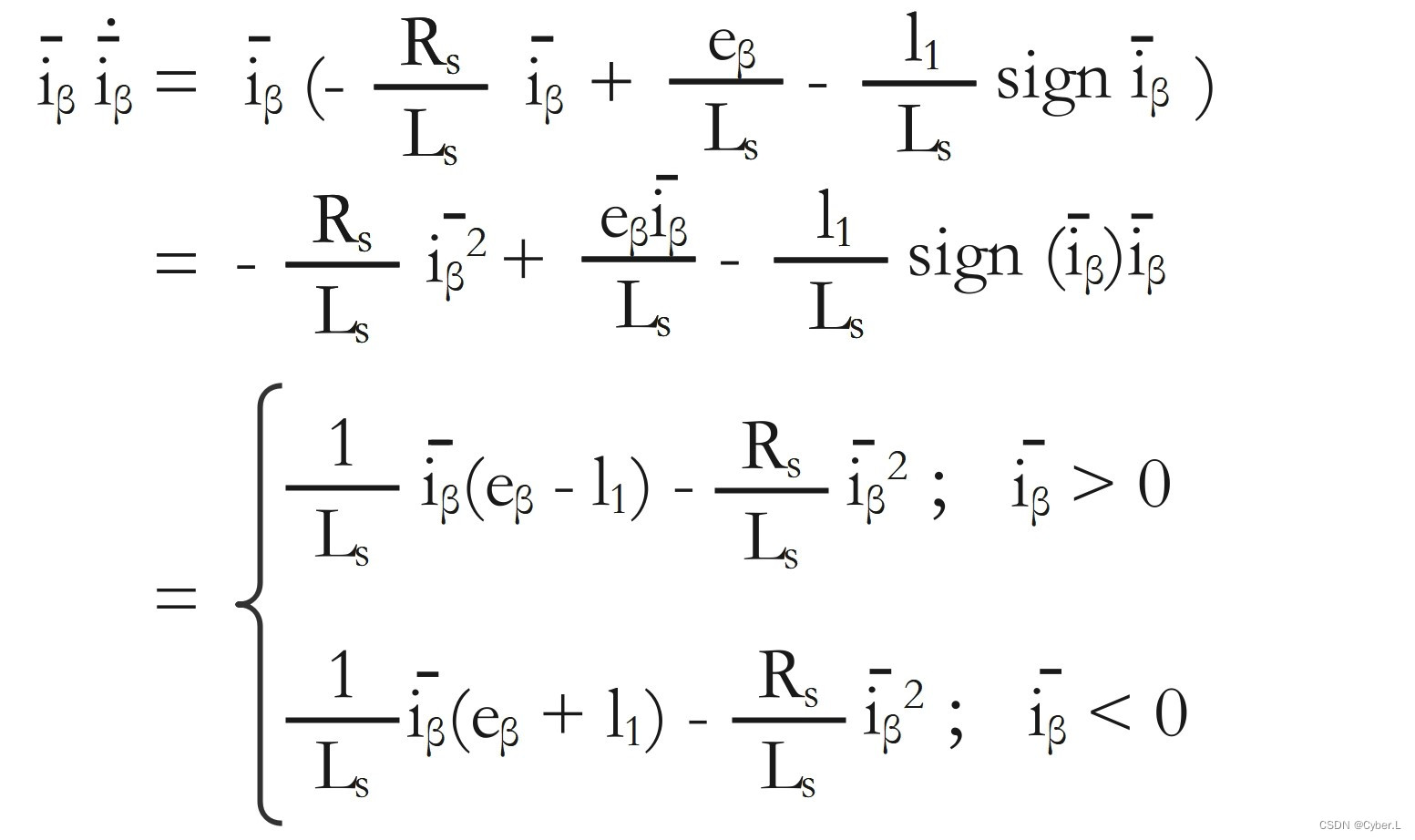
????????滑模到达条件为![]() ,即要同时满足:
,即要同时满足:

???????
????????可见只有当![]() 时,上述条件均满足,这样就可保证误差方程的渐进稳定。
时,上述条件均满足,这样就可保证误差方程的渐进稳定。
??????? 但是在实际应用中不能取的过大,否则会增加抖振噪声,引起不必要的估计误差。
2.3 估计αβ轴反电动势
????????当发生滑动模态运动时,随着S = 0,S˙ = 0,等效控制开始起作用:

????????正是在其作用下,使得定子电流估计值跟踪到实际值,从而使得等效控制分量与 电机反电动势保持一致,起到观测反电动势的效果。(这里有人可能会觉得观测的ueqα、ueqβ只有+l1和-l1这两个值。但是这样理解是有问题的,因为这里其实是类似PWM的等效控制,举个PWM波的例子,当你在一个开关周期内高频的切换开关状态让一个周期内有25%的时间10V的直流电压源加给灯泡,剩下的时间切断开关,灯泡宏观上发出的光亮就对应2.5v电压供电下灯泡的亮度。这个地方原理是一样的,观测器的控制输入反复切换自己的正负号使观测器收敛到真实值。)
????????![]() 是电流误差的开关信号,不仅包含了反电动势的信息,而且含有控制产生的高频信号,将切换控制量经过低通滤波后得到等效控制量,即估计反电动势
是电流误差的开关信号,不仅包含了反电动势的信息,而且含有控制产生的高频信号,将切换控制量经过低通滤波后得到等效控制量,即估计反电动势![]() :
:

?????????式中ω0为截止频率,不同转子速度下低通滤波器的截止频率是不一样的, 截止频率ω0和转子电角速度ωr存在如下关系:

????????式中一般取K为1~2范围内的数值。
2.4 转子位置和转速计算
??????? 通过第一节的讲解中我们知道,反电动势中包含了,转子转速及角度相关的信息,如下图所示:

????????转子位置信号可以从估计反电动势中提取出来:
![]()
????????由于低通滤波特性会带来一定的相位滞后,因此有必要在实际应用中对相位 进行滞后补偿:

????????其中Δθ为补偿量,ω'为转子观测转速,ω0为滤波器截止频率。
????????转子转速ωr = ω'为:

3. 总结
????????滑模观测器提供了一种有效的方法来实现无位置传感器控制,通过观测电机的αβ轴的反电动势,从而计算出电机的转子位置和速度信息。滑模观测器的一个重要优点是其对系统参数变化和外部扰动具有良好的鲁棒性。由于滑模控制的特性,即使在存在不确定性或噪声的情况下,一旦系统进入滑动模式,观测误差能够迅速减小并保持在可接受的范围内。
??????? 除了通过反电动势直接计算出角度和转速以外,也可以通过锁相环来获取,在下一章节我会来讲解PLL锁相环在滑模观测器中的应用,教大家如何通过锁相环获取到角度和转速。
????????
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!