Simpy简介：python仿真模拟库-02/5

二、SymPy — 简化（Simplification）

?

????????SymPy 擅长通过其多样化的简化函数来简化数学表达式。在 SymPy 中，您会发现通用的 Simply() 函数，专用于实现表达式最直接的表示。

????????简化Simplification：simple() 函数位于 sympy.simplify 模块中，旨在使用启发式方法增强输入表达式的简单性。一个例子通过简化表达式 sin2(x) + cos2(x) 来演示其用法。

from sympy import * 
x=Symbol('x')
expr=sin(x)**2 + cos(x)**2 
simplify(expr)

Output:
1

三、 展开Expand

????????Expand() 是 SymPy 中最常见的简化函数之一，用于展开多项式表达式。例如 -

a,b=symbols('a b') 
expand((a+b)**2)

expand((a+b)*(a-b))

????????Expand() 函数通常会增加表达式的大小，尽管它在应用时偶尔会减小表达式的大小。一般来说，调用expand()可能会导致更大的表达式，但也有例外，它会简化它们。

expand((x + 1)*(x - 2) - (x - 1)*x)

Output:
-2

四、因式分解

????????该函数接受多项式并将其分解为有理数领域内的不可约分量。

x,y,z=symbols('x y z') 
expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
factor(expr)

factor(x**2+2*x+1)

????????Factor() 函数是 Expand() 的逆函数，并保证不可约因子。Factor_list() 提供因子的结构化输出。

expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
factor_list(expr)

Output:
(1, [(z, 1), (x + 2*y, 2)])

五、收集collect

????????该函数根据表达式列表收集表达式的加法分量，并考虑有理指数幂。

expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 
expr

六、取消

????????cancel() 函数的目的是将任何有理函数转换为常规格式 p/q，其中 p 和 q 都是没有共享因子的展开多项式表达式。此外，p 和 q 的前导系数是整数，缺少小数部分。

expr1=x**2+2*x+1 
expr2=x+1 
cancel(expr1/expr2)

Output:
x+1

expr = 1/x + (3*x/2 - 2)/(x - 4) 
expr

cancel(expr)

七、trigsimp（三角恒等式）

????????该函数的目的是简化三角恒等式。值得一提的是，反三角函数的命名约定包括在函数名称中添加“a”作为前缀。例如，反余弦表示为“acos()”。

from sympy import trigsimp, sin, cos 
from sympy.abc import x, y
expr = 2*sin(x)**2 + 2*cos(x)**2 
trigsimp(expr)

Output:
2

????????trigsimp 函数使用启发式方法来应用最合适的三角恒等式。

八、指数项简化

该函数通过组合具有相似底数和指数的幂来简化给定的表达式。

expr=x**y*x**z*y**z 
expr

powsimp(expr)

????????您可以通过两种方式控制 powsimp() 的操作方式：仅合并底数或仅合并指数。默认的“全部”模式结合了底数和指数。将“force”设置为 True 会合并基础而不考虑假设。

powsimp(expr, combine='base', force=True)

九、梳子Combsimp

????????您可以使用 SymPy 的 Combsimp() 函数简化涉及阶乘和二项式的组合表达式。此外，SymPy 还提供了专用的 Factorial() 函数来处理阶乘。

expr=factorial(x)/factorial(x - 3) 
expr

为了简化上面的组合表达式，我们使用 Combsimp() 函数，如下所示 -

combsimp(expr)

十、对数组合

该函数采用对数并使用以下规则组合它们 -

• log(x) + log(y) == log(x*y) 如果两者均为正数
• a*log(x) == log(x**a) 如果 x 为正且 a 为实数

logcombine(a*log(x) + log(y) - log(z))

当此功能中启用“force”参数时，除非对数量存在现有假设，否则它将假设上述条件有效。

logcombine(a*log(x) + log(y) - log(z), force=True)

十一、SymPy — 导数

????????函数的导数表示其变量之一的变化速度。这对应于确定特定点处切线的斜率。在 SymPy 中，您可以使用“diff()”函数计算带有变量的数学表达式的微分。

diff(expr, variable)
from sympy import diff, sin, exp 
from sympy.abc import x,y 
expr=x*sin(x*x)+1 >>> expr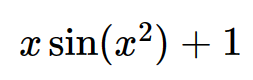

diff(expr,x)

diff(exp(x**2),x)

要计算多重导数，只需重复每个微分步骤的变量或通过在变量后指定数值来指示所需的顺序。

diff(x**4,x,3)

Output:
24x

for i in range(1,4): print (diff(x**4,x,i))

Output:
4*x**3
12*x**2
24*x

????????也可以调用表达式的 diff() 方法。它的工作原理与 diff() 函数类似。

expr=x*sin(x*x)+1 
expr.diff(x)

????????SymPy 中的 Derivative 类允许您创建未计算的导数，与 diff() 函数共享相同的语法。要获得该导数的实际结果，您可以应用 doit 方法。

from sympy import Derivative 
d=Derivative(expr) 
d

d.doit()

十二、SymPy — 集成

????????在 SymPy 包中，您将找到积分模块，该模块设计用于计算数学表达式的定积分和不定积分。当在表达式后面提供变量时，integrate() 方法可以计算原始积分或不定积分。

integrate(f, x)

????????要计算定积分，请按如下方式传递参数 -

(integration_variable, lower_limit, upper_limit)

from sympy import * 
x,y = symbols('x y') 
expr=x**2 + x + 1 
integrate(expr, x)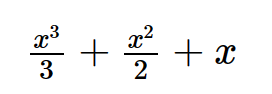

expr=sin(x)*tan(x) 
expr 
integrate(expr,x)

expr=exp(-x**2) 
integrate(expr,(x,0,oo) )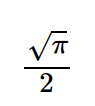

????????您可以使用 Integral 对象创建未计算的积分，该对象可以通过调用 doit() 方法进行计算。

expr = Integral(log(x)**2, x) 
expr

expr.doit()

十三、积分变换

SymPy 支持各种类型的积分变换，如下所示 -

• 拉普拉斯变换
• 傅里叶变换
• 正弦变换
• 余弦变换
• 汉克尔变换

提到的函数位于 sympy.integrals.transforms 模块内。提供的示例说明了傅立叶变换和拉普拉斯变换的计算。

实施例1

from sympy import fourier_transform, exp 
from sympy.abc import x, k 
expr=exp(-x**2) 
fourier_transform(expr, x, k)

在 python shell 中执行上述命令时，将生成以下输出 -

sqrt(pi)*exp(-pi**2*k**2)

这相当于 -

实施例2

from sympy.integrals import laplace_transform 
from sympy.abc import t, s, a 
laplace_transform(t**a, t, s)

在 python shell 中执行上述命令时，将生成以下输出 -

(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)

十四、SymPy — 矩阵

????????在数学领域，矩阵是元素的结构化排列，可以包含数字、符号或数学表达式。矩阵运算的概念涉及对这些矩阵结构执行各种数学运算，所有这些运算都遵循特定的数学准则。

????????矩阵的一个值得注意的应用在于线性变换领域，这是许多科学学科中的一个重要概念，特别是在基于矩阵的方法学广泛应用的物理领域。

????????在 SymPy 包中，有一个用于处理矩阵的专用模块。该模块介绍了 Matrix 类，它是一个基本组件，可用作矩阵的表示并促进矩阵的操作。

from sympy.matrices import Matrix

from sympy.matrices import Matrix 
m=Matrix([[1,2,3],[2,3,1]]) 
m

????????矩阵是从适当大小的列表对象创建的。您还可以通过将列表项分布在指定数量的行和列中来获取矩阵。

M=Matrix(2,3,[10,40,30,2,6,9]) 
M

矩阵是一个可变对象。矩阵模块还提供了 ImmutableMatrix 类来获取不可变矩阵。

十五、基本操控

Matrix 对象的shape属性返回其大小。

M.shape

Output:
(2,3)

row() 和 col() 方法分别返回指定数量的行或列。

M.row(0)

Output:
[10 40 30]

M.col(1)

使用 Python 的切片运算符来获取属于行或列的一项或多项。

M.row(1)[1:3]

Output:
[6, 9]

Matrix 类具有 row_del() 和 col_del() 方法，可从给定矩阵中删除指定的行/列 -

M=Matrix(2,3,[10,40,30,2,6,9]) 
M.col_del(1) 
M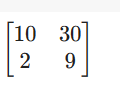

您可以使用以下命令将样式应用于输出 -

M.row_del(0) 
M

Output:
[2  6  9]

类似地，row_insert() 和 col_insert() 方法在指定的行或列索引处添加行或列

M1=Matrix([[10,30]]) 
M=M.row_insert(0,M1)
M

十六、算术运算

????????定义常用运算符 +、— 和 * 来执行加法、减法和乘法。

M1=Matrix([[1,2,3],[3,2,1]]) 
M2=Matrix([[4,5,6],[6,5,4]]) 
M1+M2

M1-M2

????????矩阵乘法可以在第一个矩阵中的列数与第二个矩阵中的行数匹配的条件下发生。此外，结果将具有与第一个矩阵相同的行数和与第二个矩阵相同的列数。

M1=Matrix([[1,2,3],[3,2,1]]) 
M2=Matrix([[4,5],[6,6],[5,4]]) 
M1*M2

十七、矩阵构造函数

????????SymPy 提供各种专门的矩阵类，例如单位矩阵和全零或全填充的矩阵。这些类分别用名称“eye”、“zeros”和“ones”表示。具体来说，单位矩阵是一个方阵，其中沿对角线的所有元素都等于 1，而所有其他元素都设置为 0。

from sympy.matrices import eye
eye(3)

????????在对角矩阵中，对角线上的元素根据提供的参数进行初始化。

from sympy.matrices import diag 
diag(1,2,3)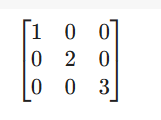

????????零矩阵中的所有元素都初始化为 0。

from sympy.matrices import zeros 
zeros(2,3)

????????同样，ones 是所有元素都设置为 1 的矩阵。

from sympy.matrices import ones
ones(2,3)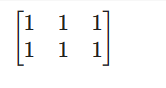

????????到目前为止，一切都很好。我们已经看到使用该库的各种简化，数学工具箱绝对是好的。在接下来的部分中，我们将了解如何定义和使用本质上构成模拟构建块的函数。