#头歌 数据结构 线性表
第2关?线性表的顺序表示和实现
任务描述
本关任务:实现 step1/Seqlist.cpp 中的SL_InsAt、SL_DelAt和SL_DelValue三个操作函数,以实现线性表中数据的插入、删除与查找等功能。
相关知识
线性表是最基本、最简单、也是最常用的一种数据结构。线性表结构中,数据元素之间通过一对一首尾相接的方式连接起来。具体实现时,线性表可以采用不同的存储策略。下面给出了一种基于顺序存储的线性表实现方案:
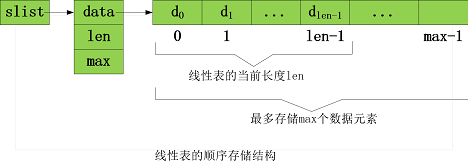
该方案将线性表存储在一片连续空间里,并通过data、len和max三个属性元素。组织成为一个结构:
data: 给出线性表存储空间的起始地址;max: 指明线性表存储空间最多可存储的数据元素个数;len: 当前线性表里的数据元素个数。
为了讨论简化,我们假设每个数据元素是一个整数:
typedef int T; // 数据元素的数据类型
该线性表的结构定义如下:
struct SeqList{T* data; // 数据元素存储空间的开始地址int len; // 线性表的当前长度int max; // 线性表的最大长度};
以上示意图中的slist是指向该结构的一个指针,只要给定slist指针,就可对线性表进行操作。
对数据元素进行操作处理是一个数据结构的重要组成部分。线性表涉及的主要操作如下:
-
创建线性表:创建一个最多可存储
max个数据元素的顺序存储的线性表,并将其初始状态设置为len=0。该操作函数具体定义如下,其返回值为slist:SeqList* SL_Create(int max) -
释放线性表存储空间:释放
slist->data所指向的用于存储线性表数据元素的存储空间。该操作函数具体定义如下:void SL_Free(SeqList* slist) -
置空线性表:将当前线性表变为一个空表,实现方法是将
slist->len设置为0。该操作函数具体定义如下:void SL_MakeEmpty(SeqList* slist) -
获取线性表当前长度:获取并返回线性表的当前长度
slist->len。该操作函数具体定义如下:int SL_Length(SeqList* slist) -
判断线性表是否为空:若当前线性表是空表,则返回
false,否则返回true。该操作函数具体定义如下:BOOL SL_IsEmpty(SeqList* slist) -
判断线性表是否已满:若线性表达到最大长度,则返回
true,否则返回false。该操作函数具体定义如下:BOOL SL_IsFull(SeqList* slist) -
返回线性表第
i个数据元素:返回线性表的第i个数据元素slist->data[i]。该操作函数具体定义如下:T SL_GetAt(SeqList* slist, int i)
-
修改线性表第
i个数据元素: 将线性表的第i个数据元素的值修改为x。该操作函数具体定义如下:void SL_SetAt(SeqList* slist, int i, T x) -
在线性表位置
i插入数据元素x: 将x插入slist->data[i]之前。若插入失败(i>slist->len或i<0时,无法插入),返回false,否则返回true。该操作函数具体定义如下:BOOL SL_InsAt(SeqList* slist, int i, T x) -
删除线性表位置
i处的数据元素: 删除线性表的i号数据元素。输入参数i范围应在[0,slist->len-1]内,否则会产生不能预料的异常或错误。返回被删除的数据元素的值。该操作函数具体定义如下:T SL_DelAt(SeqList* slist, int i) -
查找线性表中第一个值为
x的数据元素的位置: 找到线性表中第一个值为x的数据元素的编号。返回值-1表示没有找到,返回值>=0表示该元素位置。该操作函数具体定义如下:int SL_FindValue(SeqList* slist, T x) -
删除线性表中第一个值为
x的数据元素: 删除第一个值为x的数据元素,返回该数据元素的编号。如果不存在值为x的数据元素,则返回-1。该操作函数具体定义如下:int SL_DelValue(SeqList* slist, T x) -
打印线性表: 打印整个线性表。该操作函数具体定义如下:
void SL_Print(SeqList* slist)
编程要求
本关任务是实现 step1/Seqlist.cpp 中的SL_InsAt、SL_DelAt和SL_DelValue三个操作函数,以实现线性表中数据的插入、删除与查找等功能。具体要求如下:
-
SL_InsAT: 在顺序表的位置i插入结点x,即插入d[i]之前,i的有效范围[0,slist->len]; -
SL_DelAt:删除顺序表slist的第i号结点,i的有效范围应在[0,slist->len)内,否则会产生异常或错误。返回被删除的数据元素的值; -
SL_DelValue:删除第一个值为x的结点,存在值为x的结点则返回结点编号,未找到返回-1; -
输入输出格式请参见后续测试样例。
注意:本关必读中提及的其他操作已经由平台实现,你在实现本关任务的三个操作函数时,在函数体内可调用其他操作。`
本关涉及的代码文件 Seqlist.cpp 中的 3 个操作函数的代码框架如下:
bool SL_InsAt(SeqList* slist, int i, T x)// 在顺序表的位置i插入结点x, 插入在d[i]之前。i的有效范围[0,slist->len]{// 请在这里补充代码,完成本关任务/********** Begin *********//********** End **********/}
T SL_DelAt(SeqList* slist, int i)// 删除顺序表slist的第i号结点(i的有效范围应在[0,slist->len)内,否则会产生异常或错误)。返回被删除的数据元素的值。{// 请在这里补充代码,完成本关任务/********** Begin *********//********** End **********/}
int SL_DelValue(SeqList* slist, T x)// 删除第一个值为x的结点。存在值为x的结点则返回结点编号, 未找到则返回-1{// 请在这里补充代码,完成本关任务/********** Begin *********//********** End **********/}
测试说明
本关的测试文件是 step1/Main.cpp ,负责对实现的代码进行测试。具体代码如下:
#include <stdio.h>#include <stdlib.h>#include "SeqList.h"#pragma warning(disable:4996)void main(){//设置线性表最多可存储的元素个数maxint max=100;//创建一个长度为max的空线性表SeqList* slist=SL_Create(max);//声明并读入线性表当前长度nint n;scanf("%d", &n);int i;int item;//循环读入n个整数,并存入到线性表中for (i=0; i<n; i++){scanf("%d", &item);SL_InsAt(slist, i, item);}//读入一个整数idel,并将线性表中位置idel处的数据元素删除int idel;scanf("%d", &idel);SL_DelAt(slist, idel);//读入一个整数整itemdel,并将线性表中第一次出现该值的数据元素删除int itemdel;scanf("%d", &itemdel);SL_DelValue(slist, itemdel);SL_Print(slist);//释放线性表空间SL_Free(slist);}
注意:step1/Main.cpp的代码不能被修改。
以下是平台对 step1/Main.cpp 的测试样例:
样例输入:
5 //输入线性表的长度8 9 12 33 45 //依次输入线性表的数据元素2 //删除线性表的2号数据元素33 //删除值为33的数据元素
样例输出 8 9 45 //输出当前线性表的数据元素
开始你的任务吧,祝你成功!
截止后通关代码:
// 顺序表操作实现文件
//
#include <stdio.h>
#include <stdlib.h>
#include "Seqlist.h"
SeqList* SL_Create(int maxlen)
// 创建一个顺序表。
// 与SqLst_Free()配对。
{
? ? SeqList* slist=(SeqList*)malloc(sizeof(SeqList));
? ? slist->data = (T*)malloc(sizeof(T)*maxlen);
? ? slist->max=maxlen;
? ? slist->len=0;
? ? return slist;
}
void SL_Free(SeqList* slist)
// 释放/删除 顺序表。
// 与SqLst_Create()配对。
{
? ? free(slist->data);
? ? free(slist);
}
void SL_MakeEmpty(SeqList* slist)
// 置为空表。
{
? ? slist->len=0;
}
int SL_Length(SeqList* slist)
// 获取长度。
{
? ? return slist->len;
}
bool SL_IsEmpty(SeqList* slist)
// 判断顺序表是否空。
{
? ? return 0==slist->len;
}
bool SL_IsFull(SeqList* slist)
// 判断顺序表是否满。
{
? ? return slist->len==slist->max;
}
T SL_GetAt(SeqList* slist, int i)
// 获取顺序表slist的第i号结点数据。
// 返回第i号结点的值。
{
? ? if(i<0||i>=slist->len) {
? ? ? ? printf("SL_GetAt(): location error when reading elements of the slist!\n"); ? ?
? ? ? ? SL_Free(slist);
? ? ? ? exit(0);
? ? }
? ? else
? ? ? ? return slist->data[i];
}
void SL_SetAt(SeqList* slist, int i, T x)
// 设置第i号结点的值(对第i号结点的数据进行写)。
{
? ? if(i<0||i>=slist->len) {
? ? ? ? printf("SL_SetAt(): location error when setting elements of the slist!\n"); ? ?
? ? ? ? SL_Free(slist);
? ? ? ? exit(0);
? ? }
? ? else
? ? ? ? slist->data[i]=x;
}
bool SL_InsAt(SeqList* slist, int i, T x)
// 在顺序表的位置i插入结点x, 插入d[i]之前。
// i 的有效范围[0,plist->len]。
{
? ? // 请在下面的Begin-End之间补充代码,插入结点。
? ? /********** Begin *********/
? ? int j;
? ? if((i<0)||(i>slist->len)) ?return false;
? ? if(slist->len==slist->max) ?return false;
? ? for(j=i+1;j<slist->len;j++)
? ? slist[j]=slist[j-1];
? ? slist->data[i]=x;
? ? slist->len++;
? ? return true;
? ? /********** End **********/
}
T SL_DelAt(SeqList* slist, int i)
// 删除顺序表plist的第i号结点。
// i的有效范围应在[0,plist->len)内,否则会产生异常或错误。
// 返回被删除的数据元素的值。
{
? ? // 在下面的Begin-End之间补充代码,删除第i号结点。
? ? /********** Begin *********/
? ? int j;
? ? if((i<0)||(i>slist->len)) ?return false;
? ? T t=slist->data[i];
? ? for(j=i;j<slist->len-1;j++)
? ? slist->data[j]=slist->data[j+1];
? ? slist->len--;
? ? return t;
? ? /********** End **********/
}
int SL_FindValue(SeqList* slist, T x)
// 在顺序表表中查找第一个值为x的结点,返回结点的编号。
// 返回值大于等于0时表示找到值为x的结点的编号,-1表示没有找到。
{
? ? int i=0;
? ? while(i<slist->len && slist->data[i]!=x) i++;
? ? if (i<slist->len) return i;
? ? else return -1;
}
int SL_DelValue(SeqList* slist, T x)
// 删除第一个值为x的结点。
// 存在值为x的结点则返回结点编号, 未找到返回-1。
{
? ? // 在下面的Begin-End之间补充代码,删除第一个值为 x 的结点。
? ? /********** Begin *********/
? ? int j=SL_FindValue(slist,x);
? ? if(j!=-1)
? ? {
? ? ? ? SL_DelAt(slist,j);
? ? }
? ? return j;
}
? ? /********** End **********/
void SL_Print(SeqList* slist)
// 打印整个顺序表。
{
? ? if (slist->len==0) {
? ? ? ? printf("The slist is empty.\n"); ? ? ? ?
? ? ? ? return;
? ? }
? ? //printf("The slist contains: ");
? ? for (int i=0; i<slist->len; i++) {
? ? ? ? printf("%d ?", slist->data[i]);
? ? }
? ? printf("\n"); ?
? ?
}
第3关:线性表的链式表示和实现
任务描述
本关任务:完成一个链接存储的线性表的小程序。
相关知识
线性表的存储也可以采用链接存储方式来实现。链接存储方式包括单链表、双链表和循环链表等形式。
下面描述了一种基于单链表的线性表实现方案:
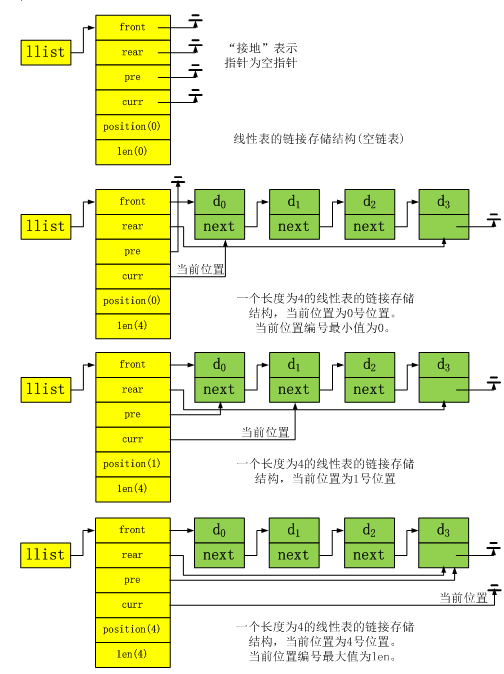
为了讨论简单,假设数据元素的类型为整型:
typedef int T;
在链表中,每个数据元素为一个链表结点,结点的具体定义为:
struct LinkNode {T data;LinkNode* next;};
如上面的单链表示意图所示,一个链表主要有front、rear、curr、position和len等属性要素组织成一个结构:
front: 指向链表的首结点;rear: 指向尾结点;curr: 指向操作的当前位置(见后文特别说明)的结点;pre: 指向当前位置的前一个结点;position: 是当前位置的编号(编号从 0 开始);len: 数据元素的个数(即链表的长度)。
基于这些属性要素,可以将线性表组织为一个链表结构:
struct LinkList {LinkNode* front; // 指向头结点LinkNode* rear; // 指向尾结点LinkNode* pre; // 指向当前位置结点的前一个结点LinkNode* curr; // 指向当前位置结点int position; // 当前位置结点的编号int len; // 线性表的大小(链表结点数)};
给定指向该结构的一个指针llist,就可以对链接存储的线性表进行操作。
特别说明:
“当前位置”:当前位置由curr指针给出,当前位置的前一个位置由pre指针给出,当前位置的编号由position给出。后面将定义的若干操作与当前位置有关,例如:在当前位置结点之前插入结点,在当前位置结点之后插入结点,等等。当为空链表时,curr和pre都为空指针,position为0。当前位置在非空链表的最左端时,pre为空指针,curr指向头结点,position=0。当前位置在非空链表的最右端时,pre指向尾结点,curr为空指针,position等于len。
针对链表数据,我们定义如下操作:
-
创建空线性表:创建一个链接存储的线性表,初始为空表,返回
llist指针。具体操作函数定义如下:LinkList* LL_Create() -
释放线性表结点:释放链表的结点,然后释放
llist所指向的结构。具体操作函数定义如下:void LL_Free(LinkList* llist) -
置空线性表:释放链表的所有结点,将当前线性表变为一个空表。具体操作函数定义如下:
void LL_MakeEmpty(LinkList* llist) -
获取线性表当前长度: 返回线性表的当前长度。具体操作函数定义如下:
int LL_Length(LinkList* llist) -
判断线性表是否为空: 若当前线性表是空表,则返回
true,否则返回false。具体操作函数定义如下:bool LL_IsEmpty(LinkList* llist) -
设置线性表当前位置: 设置线性表的当前位置为
i号位置。设置成功,则返回true,否则返回false(线性表为空,或i不在有效范围)。假设线性表当前长度为len,那么i的有效范围为[0,len]。具体操作函数定义如下:bool LL_SetPosition(LinkList* llist, int i) -
获取线性表当前位置结点编号: 获取线性表的当前位置结点的编号。具体操作函数定义如下:
int LL_GetPosition(LinkList* llist) -
设置线性表当前位置的下一位置为当前位置: 设置成功,则返回
true,否则返回false(线性表为空,或当前位置为表尾)。具体操作函数定义如下:bool LL_NextPosition(LinkList* llist) -
获取线性表当前位置的数据元素的值: 具体操作函数定义如下:
T LL_GetAt(LinkList* llist) -
修改线性表当前位置数据元素的值: 将线性表的当前位置的数据元素的值修改为
x。具体操作函数定义如下:void LL_SetAt(LinkList* llist, T x) -
在线性表当前位置之前插入数据元素: 在线性表的当前位置之前插入数据元素
x。空表允许插入,当前位置指针将指向新结点。若插入失败,返回false,否则返回true。具体操作函数定义如下:bool LL_InsAt(LinkList* llist, T x) -
在线性表当前位置之后插入数据元素: 在线性表的当前位置之后插入数据元素
x。空表允许插入,当前位置指针将指向新结点。若插入失败,返回false,否则返回true。具体操作函数定义如下:bool LL_InsAfter(LinkList* llist, T x) -
删除线性表当前位置数据元素结点: 若删除失败(为空表),则返回
false,否则返回true。具体操作函数定义如下:bool LL_DelAt(LinkList* llist) -
删除线性表当前位置后面的那个数据元素结点: 若删除失败(为空表,或当前位置是表尾),则返回
false,否则返回true。具体操作函数定义如下:bool LL_DelAfter(LinkList* llist) -
查找线性表中第一个值为
x的数据元素的编号: 返回值-1表示没有找到,返回值>=0表示编号。具体操作函数定义如下:int LL_FindValue(LinkList* llist, T x) -
删除线性表中第一个值为
x的数据元素: 删除第一个值为x的数据元素,返回该数据元素的编号。如果不存在值为x的数据元素,则返回-1。具体操作函数定义如下:int LL_DelValue(LinkList* llist, T x) -
打印整个线性表: 具体操作函数定义如下:
void LL_Print(LinkList* llist)
编程要求
本关任务是实现 step2/LinkList.cpp中的LL_InsAfter操作函数,以实现线性表数据插入功能。具体要求如下:
-
在线性表的当前位置之后插入数据元素
x。空表允许插入,当前位置指针将指向新结点。若插入失败,返回false,否则返回true; -
输入输出格式请参见后续测试样例。
注意:本关必读中提及的其他操作函数已经由平台实现,你在实现操作函数LL_InsAfter时,在函数体内可调用其他操作函数。
本关涉及的 LinkList.cpp 中的LL_InsAfter操作函数的代码框架如下:
bool LL_InsAfter(LinkList* llist, T x)// 在线性表的当前位置之后插入数据元素x。空表允许插入。当前位置指针将指向新结点。若插入失败,返回false,否则返回true。{// 请在这里补充代码,完成本关任务/********** Begin *********//********** End **********/}
测试说明
本关的测试文件是 step2/Main.cpp ,负责对你实现的代码进行测试。具体代码如下:
#include <stdio.h>#include <stdlib.h>#include "LinkList.h"#pragma warning(disable:4996)int main(){//创建一个线性表LinkList* llist=LL_Create();//向线性表中插入a个数据元素int i;int x;int a;scanf("%d", &a);for(i=0; i<a; i++) {scanf("%d",&x);LL_InsAfter(llist,x);}//设置线性表当前位置为0LL_SetPosition(llist, 0);//在线性表表头顺序插入a个元素scanf("%d", &a);for(i=0; i<a; i++) {scanf("%d", &x);LL_SetPosition(llist,0);LL_InsAfter(llist,x);}//删除线性表中第一个值为x的元素节点scanf("%d", &x);LL_DelValue(llist, x);//设置当前位置为i,并删除该位置的元素节点scanf("%d", &i);LL_SetPosition(llist, i);LL_DelAt(llist);//打印整个线性表然后释放线性表空间LL_Print(llist);system("PAUSE");LL_Free(llist);}
注意: step2/Main.cpp 的代码不能被修改。
以下是平台对 step2/Main.cpp 的测试样例: 样例输入:
3 //输入一个数a,后面将输入a个数据元素8 9 3 //a个数据元素,依次插入尾结点后。形成单链表结点序列:8,9,33 //输入一个数b,后面将再输入b个数据元素10 89 22 //b个数据元素,依次插入0号结点后。形成单链表结点序列:8,22,89,10,9,389 //删除一个值为89的结点1 //删除1号结点
样例输出 8 10 9 3
开始你的任务吧,祝你成功!
截止后通关代码:
/*************************************************************
? ? date: April 2017
? ? copyright: Zhu En
? ? DO NOT distribute this code without my permission.
**************************************************************/
// 单链表实现文件
#include <stdio.h>
#include <stdlib.h>
#include "LinkList.h"
// 1)
LinkList* LL_Create()
// 创建一个链接存储的线性表,初始为空表,返回llist指针。
{
? ? LinkList* llist=(LinkList*)malloc(sizeof(LinkList));
? ? llist->front=NULL;
? ? llist->rear=NULL;
? ? llist->pre=NULL;
? ? llist->curr=NULL;
? ? llist->position=0;
? ? llist->len=0;
? ? return llist;
}
// 2) ?
void LL_Free(LinkList* llist)
// 释放链表的结点,然后释放llist所指向的结构。
{
? ? LinkNode* node=llist->front;
? ? LinkNode* nextnode;
? ? while(node){
? ? ? ? nextnode=node->next;
? ? ? ? free(node);
? ? ? ? node=nextnode;
? ? }
? ? free(llist);
}
// 3) ?
void LL_MakeEmpty(LinkList* llist)
// 将当前线性表变为一个空表,因此需要释放所有结点。
{
? ? LinkNode* node=llist->front;
? ? LinkNode* nextnode;
? ? while(node){
? ? ? ? nextnode=node->next;
? ? ? ? free(node);
? ? ? ? node=nextnode;
? ? }
? ? llist->front=NULL;
? ? llist->rear=NULL;
? ? llist->pre=NULL;
? ? llist->curr=NULL;
? ? llist->position=0;
? ? llist->len=0;
}
// 4) ?
int LL_Length(LinkList* llist)
// 返回线性表的当前长度。
{
? ? return llist->len;
}
// 5) ?
bool LL_IsEmpty(LinkList* llist)
// 若当前线性表是空表,则返回true,否则返回 False。
{
? ? return llist->len==0;
}
// 6) ?
bool LL_SetPosition(LinkList* llist, int i)
// 设置线性表的当前位置为i号位置。
// 设置成功,则返回true,否则返回false(线性表为空,或i不在有效的返回)。
// 假设线性表当前长度为len,那么i的有效范围为[0,len]。
{ ?
? ? int k;
? ? /* 若链表为空,则返回*/
? ? if (llist->len==0) return false;
? ? /*若位置越界*/
? ? if( i < 0 || i > llist->len)
? ? { ? printf("LL_SetPosition(): position error");
? ? ? ? return false;
? ? }
? ? /* 寻找对应结点*/
? ? llist->curr = llist->front;
? ? llist->pre = NULL;
? ? llist->position = 0;
? ? for ( k = 0; k < i; k++) ? ?{
? ? ? ? llist->position++;
? ? ? ? llist->pre = llist->curr;
? ? ? ? llist->curr = (llist->curr)->next;
? ? }
? ?
? ? /* 返回当前结点位置*/
? ? return true;
}
// 7) ?
int LL_GetPosition(LinkList* llist)
// 获取线性表的当前位置结点的编号。
{
? ? return llist->position;
}
// 8) ?
bool LL_NextPosition(LinkList* llist)
// 设置线性表的当前位置的下一个位置为当前位置。
// 设置成功,则返回true,否则返回false(线性表为空,或当前位置为表尾)。
{
? ? if (llist->position >= 0 && llist->position < llist->len)
? ? /* 若当前结点存在,则将其后继结点设置为当前结点*/
? ? {
? ? ? ? llist->position++;
? ? ? ? llist->pre = llist->curr;
? ? ? ? llist->curr = llist->curr->next;
? ? ? ? return true;
? ? }
? ? else
? ? ? ? return false;
}
// 9) ?
T LL_GetAt(LinkList* llist)
// 返回线性表的当前位置的数据元素的值。
{
? ? if(llist->curr==NULL)
? ? {
? ? ? ? printf("LL_GetAt(): Empty list, or End of the List.\n");
? ? ? ? LL_Free(llist);
? ? ? ? exit(1);
? ? }
? ? return llist->curr->data;
}
// 10) ?
void LL_SetAt(LinkList* llist, T x)
// 将线性表的当前位置的数据元素的值修改为x。
{
? ? if(llist->curr==NULL)
? ? {
? ? ? ? printf("LL_SetAt(): Empty list, or End of the List.\n");
? ? ? ? LL_Free(llist);
? ? ? ? exit(1);
? ? }
? ? llist->curr->data=x;
}
// 11) ?
bool LL_InsAt(LinkList* llist, T x)
// 在线性表的当前位置之前插入数据元素x。当前位置指针指向新数据元素结点。
// 若插入失败,返回false,否则返回true。
{ ?
? ? LinkNode *newNode=(LinkNode*)malloc(sizeof(LinkNode));
? ? if (newNode==NULL) return false;
? ? newNode->data=x;
? ? if (llist->len==0){
? ? ? ? /* 在空表中插入*/
? ? ? ? newNode->next=NULL;
? ? ? ? llist->front = llist->rear = newNode;
? ? }
? ? //当前位置为表头。
? ? else if (llist->pre==NULL)
? ? {
? ? ? ? /* 在表头结点处插入*/
? ? ? ? newNode->next = llist->front;
? ? ? ? llist->front = newNode;
? ? }
? ? else { ?
? ? ? ? /* 在链表的中间位置或表尾后的位置插入*/
? ? ? ? newNode->next = llist->curr;
? ? ? ? llist->pre->next=newNode;
? ? }
? ? //插入在表尾后。
? ? if (llist->pre==llist->rear)
? ? ? ? llist->rear=newNode;
? ? /* 增加链表的大小*/
? ? llist->len++;
? ? /* 新插入的结点为当前结点*/
? ? llist->curr = newNode;
? ? return true;
}
// 12) ?
bool LL_InsAfter(LinkList* llist, T x)
// 在线性表的当前位置之后插入数据元素x。空表允许插入。当前位置指针将指向新结点。
// 若插入失败,返回false,否则返回true。
{
? ? // 请在Begin-End之间补充代码,实现结点插入。
? ? /********** Begin *********/
? ? LinkNode * newNode=(LinkNode*)malloc(sizeof(LinkNode));
? ? if(newNode==NULL) return false;
? ? newNode->data=x;
? ? if(llist->len==0)
? ? {
? ? //在空表插入
? ? ? ? newNode->next=NULL;
? ? ? ? llist->front=llist->rear=newNode;
? ? }
? ? else if(llist->curr==llist->rear)
? ? {
? ? ? ? //在尾结点插入
? ? ? ? newNode->next=NULL;
? ? ? ? llist->rear->next=newNode;
? ? ? ? llist->pre=llist->rear;
? ? ? ? llist->rear=newNode;
? ? ? ? llist->position=llist->len;
? ? }
? ? else
? ? { ?
? ? ? ? //在中间插入
? ? ? ? newNode->next=llist->curr->next;
? ? ? ? llist->curr->next=newNode;
? ? ? ? llist->pre=llist->curr;
? ? ? ? llist->position++;
? ? }
? ? llist->len++;//增加链表的长度
? ? llist->curr=newNode;
? ? return true;
? ? /********** End **********/
}
// 13) ?
bool LL_DelAt(LinkList* llist)
// 删除线性表的当前位置的数据元素结点。
// 若删除失败(为空表,或当前位置为尾结点之后),则返回false,否则返回true。
{ ?
? ? LinkNode *oldNode;
? ? /* 若表为空或已到表尾之后,则给出错误提示并返回*/
? ? if (llist->curr==NULL)
? ? { ?
? ? ? ? printf("LL_DelAt(): delete a node that does not exist.\n");
? ? ? ? return false;
? ? }
? ? oldNode=llist->curr;
? ? /* 删除的是表头结点*/
? ? if (llist->pre==NULL)
? ? { ?
? ? ? ? llist->front = oldNode->next;
? ? }
? ? /* 删除的是表中或表尾结点*/
? ? else if(llist->curr!=NULL){
? ? ? ? llist->pre->next = oldNode->next;
? ? }
? ? if (oldNode == llist->rear) {
? ? ? ? /* 删除的是表尾结点,则修改表尾指针和当前结点位置值*/
? ? ? ? llist->rear = llist->pre;
? ? }
? ? /* 后继结点作为新的当前结点*/
? ? llist->curr = oldNode->next;
? ? /* 释放原当前结点*/
? ? free(oldNode);
? ? /* 链表大小减*/
? ? llist->len --;
? ? return true;
}
// 14) ?
bool LL_DelAfter(LinkList* llist)
// 删除线性表的当前位置的后面那个数据元素。
// 若删除失败(为空表,或当前位置时表尾),则返回false,否则返回true。
{
? ? LinkNode *oldNode;
? ? /* 若表为空或已到表尾,则给出错误提示并返回*/
? ? if (llist->curr==NULL || llist->curr== llist->rear)
? ? {
? ? ? ? printf("LL_DelAfter(): ?delete a node that does not exist.\n");
? ? ? ? return false;
? ? }
? ? /* 保存被删除结点的指针并从链表中删除该结点*/
? ? oldNode = llist->curr->next;
? ? llist->curr->next=oldNode->next;
? ?
? ? if (oldNode == llist->rear)
? ? ? ? /* 删除的是表尾结点*/
? ? ? ? llist->rear = llist->curr;
? ? /* 释放被删除结点*/
? ? free(oldNode);
? ? /* 链表大小减*/
? ? llist->len --;
? ? return true;
}
// 15) ?
int LL_FindValue(LinkList* llist, T x)
// 找到线性表中第一个值为x的数据元素的编号。
// 返回值-1表示没有找到,返回值>=0表示编号。
{
? ? LinkNode* p=llist->front;
? ? int idx=0;
? ? while(p!=NULL && p->data!=x) {
? ? ? ? idx++;
? ? ? ? p = p->next;
? ? }
? ? if (idx>=llist->len) return -1;
? ? else return idx;
}
// 16) ?
int LL_DelValue(LinkList* llist, T x)
// 删除第一个值为x的数据元素,返回该数据元素的编号。如果不存在值为x的数据元素,则返回-1。
{
? ? int idx=LL_FindValue(llist, x);
? ? if (idx<0) return -1;
? ? LL_SetPosition(llist, idx);
? ? LL_DelAt(llist);
? ? return idx;
}
// 17) ?
void LL_Print(LinkList* llist)
// 打印整个线性表。
{
? ? LinkNode* node=llist->front;
? ? while (node) {
? ? ? ? printf("%d ", node->data);
? ? ? ? node=node->next;
? ? }
? ? printf("\n");
}
第4关:线性链表
任务描述
本关任务:根据所学线性链表的基础知识,完成线性链表插入数据功能的程序编写并通过所有测试用例。
相关知识
为了完成本关任务,你需要掌握:
1、线性链表的基础知识;
2、线性链表的实现。
线性链表简介
线性表的链式存储结构称为线性链表,如图1所示,线性链表将存储空间划分成若干的小块,每块占用若干个字节,这些小块称为存储结点。将其中的存储结点分为两个部分,一部分用于存储数据元素的值,称为数据域;另一部分用于存储元素之间的前后件关系,即存放下一个元素在存储序号(存储地址),指向后件结点。在线性链表中用一个专门的指针 HEAD 指向线性链表中第一个数据元素的结点(即存放第一个元素的地址)。线性表中最后一个元素没有后件,因此,线性链表中的最后一个结点的指针域为空(用 NULL 或0表示),表示链终结。
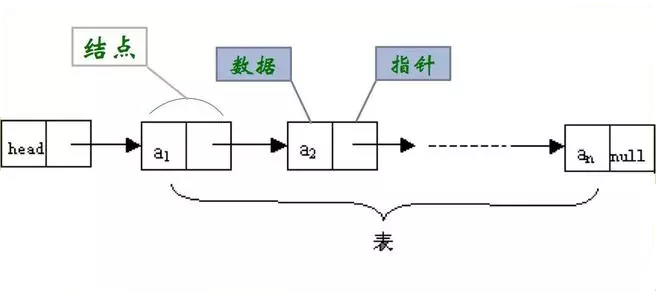
图 1 线性链表
线性链表中各元素的存储序号是不连续的,元素间的前后件关系与位置关系同时也是不一致的,前后件的关系依靠各结点的指针来指示,指向表的第一个元素的指针 HEAD 称为头指针,当HEAD=NULL时,表示该链表为空。对于线性链表,可以从头指针开始,沿着各结点的指针扫描到链表中的所有结点。这种线性链表称为线性单链表,即可以从表头开始向后扫描链表中的所有结点,而不能从中间或表尾结点向前扫描位于该结点之前的元素。
线性链表的实现
1、插入结点
当需要向链表中插入结点时,根据插入位置的不同,可分为3种情形:插入到链表的首部,也就是头结点和首元结点中间;插入到链表中间的某个位置;插入到链表最末端。虽然插入位置有区别,但使用的插入方法是一样的,如图2所示,首先,需要将新结点的 next 指针指向所插入位置后的结点;再插入位置前的结点的 next 指针指向插入结点,即可完成插入操作。
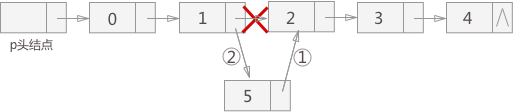
图 2 插入结点
代码示例:
link * insertElem(link * p,int elem,int add){link * temp=p; //创建临时结点temp//首先找到要插入位置的上一个结点for (int i=1; i<add; i++) {if (temp==NULL) {printf("插入位置无效\n");return p;}temp=temp->next;}//创建插入结点clink * c=(link*)malloc(sizeof(link));c->elem=elem;//向链表中插入结点c->next=temp->next;temp->next=c;return p;}
2、查找与更新
当需要查找线性链表的某个数据时,一般情况下,链表只能通过头结点或者头指针进行访问,所以实现查找某结点最常用的方法就是对链表中的结点进行逐个遍历。代码示例如下:
int selectElem(link * p,int elem){link * t=p;int i=1;while (t->next) {t=t->next;if (t->elem==elem) {return i;}i++;}return -1;}
若需要对链表中的某个结点数据进行修改与更新,首先我们需要通过遍历的方式找到对应的结点,再对其数据域进行更新即可。代码示例如下:
//更新函数,其中,add 表示更改结点在链表中的位置,newElem 为新的数据域的值link *amendElem(link * p,int add,int newElem){link * temp=p;temp=temp->next;//在遍历之前,temp指向首元结点//遍历到被删除结点for (int i=1; i<add; i++) {temp=temp->next;}temp->elem=newElem;return p;}
编程要求
在右侧编辑器中的 Begin-End 之间补充 C 语言代码,完成对线性链表插入功能的实现,其数据内容通过 scanf 从后台获取。
测试说明
平台将使用测试集运行你编写的程序代码,若全部的运行结果正确,则通关。
测试输入:
张三李四王五
预期输出:
线性链表创建成功!张三李四王五
开始你的任务吧,祝你成功!
截止后通关代码:
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
struct stu{
? ? char ?name[32];
? ? struct stu ?*next;
};
/*创建链表,参数n是初始化链表时建立的数据个数
prev:指向当前结点的前一个结点
cur:指向当前结点
head:保存表头结点的指针*/
struct stu* CreatList(int n){
? ? int i;
? ? struct stu *prev,*cur,*head;
? ? head=(struct stu*)malloc(sizeof(struct stu));
? ? if(head==NULL){
? ? ? ? printf("Can't alloc memory\n");
? ? ? ? return NULL;
? ? }
? ? prev=head;
? ? head->name[0]='\0';
? ? head->next=NULL;
? ? for(i=1;i<=n;i++){
? ? ? ? cur=(struct stu*)malloc(sizeof(struct stu));
? ? ? ? if(cur==NULL){
? ? ? ? ? ? printf("Can't alloc memory\n");
? ? ? ? ? ? return NULL; ? ? ? ? ? ? ? ?
? ? ? ? }
? ? scanf("%s",cur->name);
? ? // 请在下面的Begin-End之间补充代码,插入结点。
? ? /********** Begin *********/
prev->next=cur;
prev=cur;
?
? ? /********** End **********/
? ? }
? ? printf("线性链表创建成功!\n");
? ? return head;
}
/*遍历链表,打印链表数据*/
void Print(struct stu *head){
? ? struct stu *cur;
? ? cur=head->next;
? ? while(cur!=NULL){
? ? ? ? printf("%s\n",cur->name);
? ? ? ? cur=cur->next;
? ? }
}
int main(){
? ? int number=3;
? ? struct stu *head;
? ? head=CreatList(number);
? ? if(head==NULL)
? ? ? ? return -1;
? ? Print(head);
? ? return 0; ?
}
第5关:循环链表
任务描述
本关任务:根据所学循环链表的基础知识,完成循环链表删除数据功能的程序编写并通过所有测试用例。
相关知识
为了完成本关任务,你需要掌握:1.如何获取数组的长度,2.如何遍历数组。
循环链表简介
简单来说,单链表像一个小巷,无论怎么样最终都能从一端走到另一端,循环链表则像一个有传送门的小巷,因为循环链表当你以为你走到结尾的时候,其实你又回到了开头。循环链表和非循环链表其实创建的过程以及思路几乎完全一样,唯一不同的是,非循环链表的尾结点指向空(NULL),而循环链表的尾指针指向的是链表的开头。通过将单链表的尾结点指向头结点的链表称之为循环单链表(Circular linkedlist)。
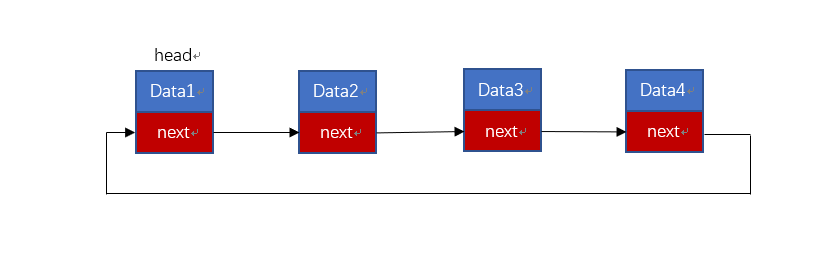
图 1 循环链表
如图1所示,循环链表将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环。循环链表与单链表的主要差异在于循环的判断上,原来是判断p->next是否为空,现在则是p->next不等于头结点,则循环未结束。
循环链表的实现
1、创建链表
如同单链表的创建,我们需要先创建一个头结点并且给其开辟内存空间,但与单链表不同的是,我们需要在开辟内存空间成功之后将头结点的next指向head自身。当需要进行插入时,我们首先创建一个新的节点,将原有链表尾结点的next指针修改指向到新的结点,新结点的next指针再重新指向头部结点,然后逐步进行这样的插入操作,最终完成整个单项循环链表的创建。代码示例如下:
int insert_list(list *head){int data; //插入的数据类型printf("请输入要插入的元素:");scanf("%d",&data);list *node=initlist();node->data=data; //初始化一个新的结点,准备进行链接if(head!=NULL){list *p=head;//找到最后一个数据while(p->next!=head){p=p->next;}p->next=node;node->next=head;return 1;}else{printf("头结点已无元素\n");return 0;}}
2、删除操作
如图2所示,循环单链表的删除操作可以参考单链表的删除操作,其都是找到需要删除的结点,将其前一个结点的next指针直接指向删除结点的下一个结点即可,但需要注意的是尾节点和头结点的特判,尤其是尾结点,因为删除尾节点后,尾节点前一个结点就成了新的尾节点,这个新的尾节点需要指向的是头结点而不是空,其重点可以记录为当前的前一节点.next=自身结点.next这样的操作可以省去头尾结点的特判。
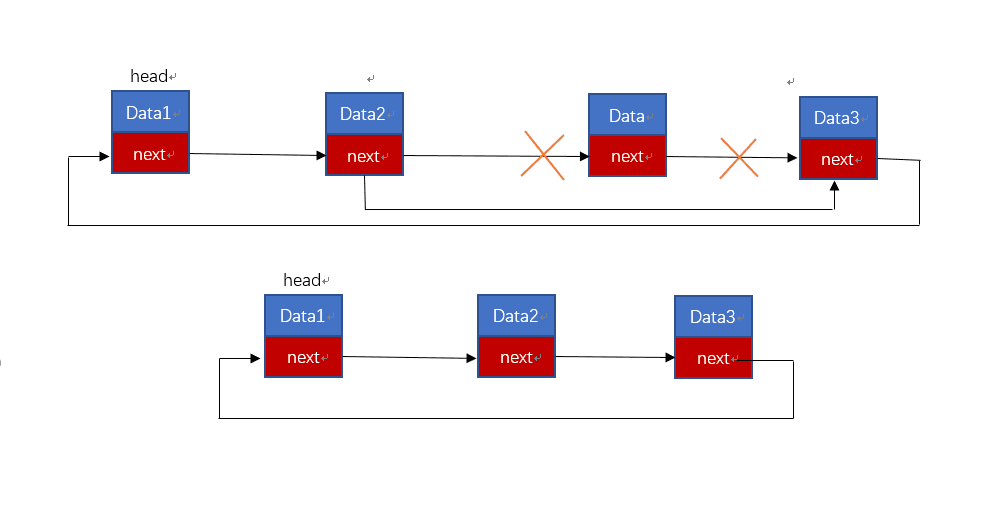
图 2 循环链表的删除操作
示例代码:
int delete_list(list *head) {if(head == NULL) {printf("链表为空!\n");return 0;}list *temp = head;list *ptr = head->next;int del;printf("请输入你要删除的元素:");scanf("%d",&del);while(ptr != head) {if(ptr->data == del) {if(ptr->next == head) {temp->next = head;free(ptr);return 1;}temp->next = ptr->next;//核心删除操作代码free(ptr);//printf("元素删除成功!\n");return 1;}temp = temp->next;ptr = ptr->next;}printf("没有找到要删除的元素\n");return 0;}
编程要求
在右侧编辑器中的 Begin-End 之间补充 C 语言代码,完成对循环链表删除功能的实现,其数据内容通过 scanf 从后台获取。
测试说明
平台将使用测试集运行你编写的程序代码,若全部的运行结果正确,则通关。
测试输入:
9 8 10 2 0 // 0是结束输入的信号
预期输出:
输入结点数据中...--------循环链表初始元素------9 8 10 2--------删除第二个结点后------9 10 2
开始你的任务吧,祝你成功!
截止后通关代码:
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include<stdlib.h>
#define ERROR 0
#define OK 1
typedef int EleType;
typedef struct CLinkNode
{
? ? EleType data;
? ? struct CLinkNode *next;
}CLinkNode,*CLinkList;
/*
初始化循环链表
*/
int InitCLinkList(CLinkList *list)
{
? ? if (list == NULL)
? ? {
? ? ? ? return ERROR;
? ? }
? ? int data = 0;
? ? CLinkNode* target = NULL;
? ? CLinkNode* head_node = NULL;
? ? printf("输入结点数据中...\n");
? ? while (1)
? ? {
? ? ? ? scanf("%d", &data);
? ? ? ? if (data == 0)
? ? ? ? {
? ? ? ? ? ? //退出循环标志,用户输入0 表示结束输入数据
? ? ? ? ? ? break;
? ? ? ? }
? ? ? ? if (*list == NULL)
? ? ? ? {
? ? ? ? ? ? CLinkNode* head= (CLinkNode*)malloc(sizeof(CLinkNode));
? ? ? ? ? ? //分配结点空间失败
? ? ? ? ? ? if (head == NULL)
? ? ? ? ? ? {
? ? ? ? ? ? ? ? exit(0);
? ? ? ? ? ? }
? ? ? ? ? ? *list = head;//链表指向头结点
? ? ? ? ? ? CLinkNode* node = (CLinkNode*)malloc(sizeof(CLinkNode));
? ? ? ? ? ? if (node == NULL)
? ? ? ? ? ? {
? ? ? ? ? ? ? ? exit(0);
? ? ? ? ? ? }
? ? ? ? ? ? node->data = data;
? ? ? ? ? ? node->next = head;
? ? ? ? ? ? head->next = node;
? ? ? ? }
? ? ? ? else
? ? ? ? {
? ? ? ? ? ? for (target = (*list)->next; target->next != *list; target = target->next);
? ? ? ? ? ? head_node = target->next;
? ? ? ? ? ? CLinkNode* node = (CLinkNode*)malloc(sizeof(CLinkNode));
? ? ? ? ? ? if (node == NULL)
? ? ? ? ? ? {
? ? ? ? ? ? ? ? exit(0);
? ? ? ? ? ? }
? ? ? ? ? ? node->data = data;
? ? ? ? ? ? node->next = head_node;
? ? ? ? ? ? target->next = node;//将新结点插入尾部
? ? ? ? }
? ? }
? ? return OK;
}
/*
往链表指定位置插入数据
list 循环链表
loc 第loc位置插入元素,loc 从1 开始计数
data 插入元素的数据域
*/
int InsertCLinkNode(CLinkList list,int loc, EleType data)
{
? ? if (list == NULL || loc < 1)
? ? ? ? return ERROR;
? ? /*
? ? 循环目的:找到第loc-1位置结点
? ? */
? ? int i = 1;
? ? CLinkNode* node = list;//刚开始node指向头结点
? ? while (node->next!=list && i < loc)
? ? {
? ? ? ? node = node->next;
? ? ? ? i++;
? ? }
? ? if (i == loc)
? ? {
? ? ? ? CLinkNode* new_node = (CLinkNode*)malloc(sizeof(CLinkNode));
? ? ? ? if (new_node == NULL)
? ? ? ? {
? ? ? ? ? ? exit(0);
? ? ? ? }
? ? ? ? new_node->data = data;
? ? ? ? new_node->next = node->next;//新结点指针域 指向前驱结点的后继结点
? ? ? ? node->next = new_node;//将新结点加入链表
? ? }
? ? else
? ? {
? ? ? ? return ?ERROR;
? ? }
? ? return OK;
}
/*
删除指定结点,通过指针返回删除结点的数据,并保存至data
*/
int DelCLinkNode(CLinkList list,int loc, EleType* data)
{
? ? if (list == NULL || loc < 1)
? ? ? ? return ERROR;
? ? /*
? ? 循环目的:找到第loc-1位置结点
? ? */
? ? int i = 1;// 按人类的读法 i表示第i个位置 和 loc 表达意思一致
? ? CLinkNode* node = list;//刚开始node指向头结点
? ? while (node->next != list && i < loc)
? ? {
? ? ? ? node = node->next;
? ? ? ? i++;
? ? }
? ? //循环结束 node 指向 loc-1 位置 且 node 不能为尾结点,为什么不能为尾结点?因为不能删除 位置上没有元素的结点!
? ? if (i == loc && node->next != list)
? ? {
? ? ? ? // 请在下面的Begin-End之间补充代码,完成对结点的删除。
? ? ? ? /********** Begin *********/
?CLinkNode* del_node = node->next;
? ? ? ? *data = del_node->data;
? ? ? ? node->next = del_node->next;
? ? ? ? free(del_node) ;
? ? ? ? /********** End **********/
? ? }
? ? return OK;
}
/*
展示循环链表元素
*/
int ShowCLinkList(CLinkList list)
{
? ? if (list == NULL)
? ? {
? ? ? ? return ERROR;
? ? }
? ? CLinkNode* target = NULL;
? ?
? ? for (target = list->next; target != list; target = target->next)
? ? ? ? printf("%d \t",target->data);
? ? printf("\n");
? ? return OK;
}
int main(int argc, char *argv[])
{
? ? int flag = 0;
? ? CLinkList list = NULL;
? ? list = NULL;
? ? InitCLinkList(&list);
? ? printf("--------循环链表初始元素------\n");
? ? ShowCLinkList(list);
? ? int loc = 2;
? ? int data = 0;
? ? DelCLinkNode(list, loc, &data);
? ? printf("--------删除第二个结点后------\n");
? ? ShowCLinkList(list);
? ? return 0;
}
第6关:双向链表
任务描述
本关任务:根据所学双向链表的基础知识,完成双向链表插入结点功能的程序编写并通过所有测试用例。
相关知识
为了完成本关任务,你需要掌握:
1、双向链表的基本概念;
2、双向链表的实现。
双向链表简介
双向链表可以简称为双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。使用这种数据结构,我们可以不再拘束于单链表的单向创建于遍历等操作,大大减少了在使用中存在的问题。

图 1 双链表结点
在单链表中,我们有一个数据域,还有一个指针域,数据域用来存储相关数据,而指针域则负责链表之间的“联系”。而在双向链表中,如图1所示,我们需要有两个指针域,一个负责向后连接,一个负责向前连接。一个完整的双向链表中应该是头结点的pre指针指为空,尾结点的next指针指向空,其余结点前后相链。双向链表中的结点可用代码表示为:
typedef struct List{int data; // 数据域struct List *next; // 向后的指针struct List *front; // 向前的指针};
双链表的实现
1、创建双链表
对于创建双向链表,我们需要先创建头结点再逐步的进行添加,请注意,双向链表的头结点是有数据元素的,也就是头结点的data域中是存有数据的,这与一般的单链表是不同的。对于逐步添加数据,我们采取的做法是,开辟一段新的内存空间作为新的结点,为这个结点的data进行赋值,然后将已有链表的上一个结点的next指针指向自身,自身的pre指针指向上一个结点。参考代码如下:
//创建双链表line* initLine(line * head){int number,pos=1,input_data;//三个变量分别代表结点数量,当前位置,输入的数据printf("请输入创建结点的大小\n");scanf("%d",&number);if(number<1){return NULL;} //输入非法直接结束head=(line*)malloc(sizeof(line)); //头结点创建head->pre=NULL;head->next=NULL;printf("输入第%d个数据\n",pos++);scanf("%d",&input_data);head->data=input_data;line * list=head;while (pos<=number) {line * body=(line*)malloc(sizeof(line));body->pre=NULL;body->next=NULL;printf("输入第%d个数据\n",pos++);scanf("%d",&input_data);body->data=input_data;list->next=body;body->pre=list;list=list->next;}return head;}
2、插入操作
对于每一次双向链表的插入操作,我们首先需要创建一个独立的结点并通过malloc操作开辟相应的空间,其次我们选中这个新创建的独立节点,将其的pre指针指向所需插入位置的前一个结点,同时,其所需插入的前一个结点的next指针修改指向为该新的结点,同理,该新的结点的next指针将会指向一个原本的下一个结点,而修改下一个结点的pre指针为指向新结点自身,这样的一个操作我们称之为双向链表的插入操作。
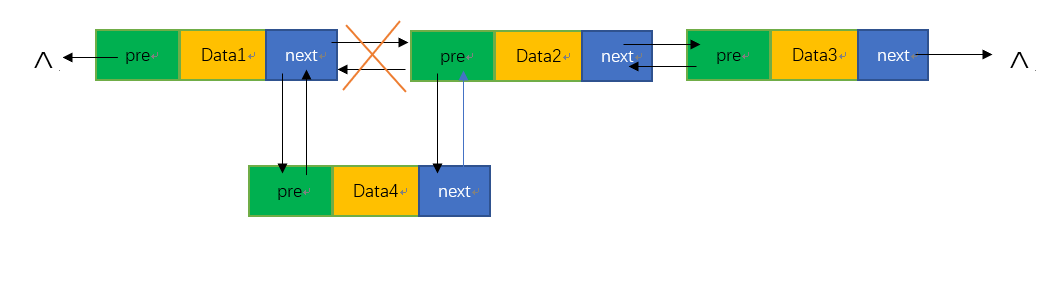
图 2 双链表的插入
3、删除操作
如图3所示,双链表的删除操作过程为:选择需要删除的结点,选中这个结点的前一个结点,将前一个结点的next指针指向自己的下一个结点,同时,选中该节点的下一个结点,将下一个结点的pre指针修改指向为自己的上一个结点,这样产生的效果就是在进行遍历的时候直接将这一个结点给跳过了。在这样的指针修改操作之后,我们释放删除结点,归还空间给内存,这样的操作我们称之为双链表的删除操作。
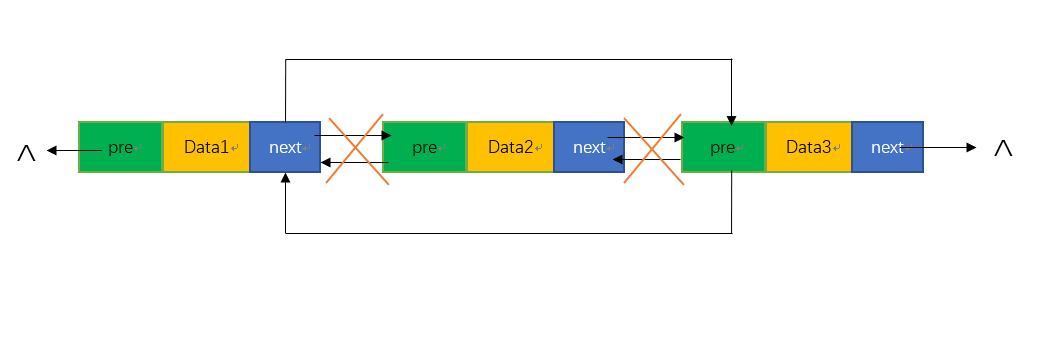
图 3 双链表的删除
4、遍历
如同单链表的遍历一样,利用next指针逐步向后进行索引即可,注意判断这里,我们既可以用while(list)的操作直接判断是否链表为空,也可以使用while(list->next)的操作判断该链表是否为空,其下一节点为空和本结点是否为空的判断条件是一样的效果,当然了,善用双向链表的pre指针进行有效的遍历也是值得去尝试的。
编程要求
在右侧编辑器中的 Begin-End 之间补充 C 语言代码,完成对双向链表插入结点功能的实现,其数据内容通过 scanf 从后台获取。
测试说明
平台将使用测试集运行你编写的程序代码,若全部的运行结果正确,则通关。
测试输入:
31 32 1 7 3 0
预期输出:
输入数据中...链表结构为:31 <-> 32 <-> 1 <-> 7 <-> 3 <-> 0链表中第 4 个节点的直接前驱是:1
开始你的任务吧,祝你成功!
截止后通关代码:
#include <stdio.h>
#include <stdlib.h>
//节点结构
typedef struct line {
? ? struct line * prior;
? ? int data;
? ? struct line * next;
}line;
//双链表的创建函数
line* initLine(line * head);
//输出双链表的函数
void display(line * head);
int main() {
? ? //创建一个头指针
? ? line * head = NULL;
? ? //调用链表创建函数
? ? head = initLine(head);
? ? printf("链表结构为:");
? ? //输出创建好的链表
? ? display(head);
? ? //显示双链表的优点
? ? printf("链表中第 4 个节点的直接前驱是:%d", head->next->next->next->prior->data);
? ? return 0;
}
line* initLine(line * head) {
? ? printf("输入数据中...\n");
? ? int data[6]={0};
? ? for(int i=0;i<6;i++){
? ? ? ? scanf("%d",&data[i]);
? ? }
? ? line * list = NULL;
? ? //创建一个首元节点,链表的头指针为head
? ? head = (line*)malloc(sizeof(line));
? ? //对节点进行初始化
? ? head->prior = NULL;
? ? head->next = NULL;
? ? head->data = data[0];
? ? //声明一个指向首元节点的指针,方便后期向链表中添加新创建的节点
? ? list = head;
? ? for (int i = 1; i <= 5; i++) {
? ? ? ? // 请在下面的Begin-End之间补充代码,插入结点,其中结点数据为data[i]。
? ? ? ? /********** Begin *********/
? ? ? ? //创建新的节点并初始化
? ? ? ? line * body = (line*)malloc(sizeof(line));
? ? ? ? body->prior = NULL;
? ? ? ? body->next = NULL;
? ? ? ? body->data = data[i];
? ? ? ? list->next = body;
? ? ? ? body->prior = list;
? ? ? ? list = list->next;
? ? ? ? /********** End **********/
? ? }
? ? //返回新创建的链表
? ? return head;
}
void display(line * head) {
? ? line * temp = head;
? ? while (temp) {
? ? ? ? //如果该节点无后继节点,说明此节点是链表的最后一个节点
? ? ? ? if (temp->next == NULL) {
? ? ? ? ? ? printf("%d\n", temp->data);
? ? ? ? }
? ? ? ? else {
? ? ? ? ? ? printf("%d <-> ", temp->data);
? ? ? ? }
? ? ? ? temp = temp->next;
? ? }
}
第7关:一元多项式的表示及相加
任务描述
本关任务:根据所学链表的基础知识,完成基于链表进行一元多项式相加的程序编写并通过所有测试用例。
相关知识
为了完成本关任务,你需要掌握:
1、如何表示一元多项式;
2、一元多项式相加。
一元多项式相加
1、任务描述
求两个一元多项式 A(x)=a0?+a1?x+a2?x2+…+an?xn 和 B(x)=b0?+b1?x+b2?x2+…+bm?xm 的和。一元多项式相加的运算规则非常简单,两个多项式中指数相同的项对应系数相加,若相加的和不为零,则构成相加结果多项式中的一项,所有指数不相同的项均复制到相加结果多项式中。
2、实现思路
通过链表实现,会更为简单直观。用链表中的每个结点表示多项式中的每一项,多项式每一项都是由数据域(包含系数和指数)和指针域构成的,所以在定义表示结点的结构体时,可如下所示进行定义:
typedef struct PLnode{//数据域,coef 表示系数,expn 表示指数float coef;int expn;//指针域struct PLnode *next;}PLnode,*PLinkList;
如图1所示,为一元多项式 A(x)=7+3x+9x8+5x17 和 B(x)=8x+22x7?9x8 的链表示意图。假设指针qa和qb分别指向多项式 A 和多项式 B 中当前进行比较的某个结点,则比较两个结点的指数项,有以下3种情况:
-
指针
qa所指结点的指数值小于指针qb所指结点的指数值,则应摘除qa所指结点插入到“和多项式”链表中去; -
指针
qa所指结点的指数值大于指针qb所指结点的指数值,则应摘除qb所指结点插入到“和多项式”链表中去; -
指针
qa所指结点的指数值等于指针qb所指结点的指数值,则将两个结点的系数相加:若和不为0,则修改qa所指结点的系数值,同时释放qb所指结点;若和为0,则应从多项式A的链表中删除相应结点,并释放指针qa和qb所指结点。

图 1 一元多项式
编程要求
在右侧编辑器中的 Begin-End 之间补充 C 语言代码,完成基于链表的一元多项式相加功能的实现,其数据内容通过 scanf 从后台获取。
测试说明
平台将使用测试集运行你编写的程序代码,若全部的运行结果正确,则通关。
测试输入:
41 92 49 17 419 2
预期输出:
La=x^9+2x^4+9x+7x^4Lb=9x^2计算结果为:Lc=9x^2+x^9+2x^4+9x+7x^4
开始你的任务吧,祝你成功!
截止后通关代码:
?#include <stdio.h>
#include <stdlib.h>
typedef struct PLnode{
? ? //数据域,coef 表示系数,expn 表示指数
? ? float coef;
? ? int expn;
? ? //指针域
? ? struct PLnode *next;
}PLnode,*PLinkList;
//一元多项式的链表表示创建函数,输入 m 项的系数和指数,建立表示一元多项式的有序链表L
void creatpolyn(PLinkList L, int m){
? ? int i;
? ? float coef;
? ? int expn;
? ? PLinkList tail,n;
? ? L->coef = m;
? ? L->expn = -1;
? ? tail = L;
? ? for(i=1 ; i<=m ; i++){
? ? ? ? ?n = (PLinkList)malloc(sizeof(PLnode));
? ? ? ? ?scanf("%f",&coef);
? ? ? ? ?scanf("%d",&expn);
? ? ? ? ?n->coef = coef;
? ? ? ? ?n->expn = expn;
? ? ? ? ?n->next = NULL;
? ? ? ? ?tail->next = n;
? ? ? ? ?tail = n;
? ? }
}
//完成多项式相加运算,即 Lc = La + Lb,并销毁一元多项式 Lb
PLinkList addpolyn(PLinkList La , PLinkList Lb){
? ? int x,len;
? ? float y;
? ? PLinkList Lc,pa,pb,pc,u;
? ? Lc = La;
? ? len = 0;
? ? pc = Lc;
? ? //另pa,pb 指向La 、Lb 的首元结点
? ? pa = La->next;
? ? pb = Lb->next;
? ? //通过 pa,pb 遍历链表 La、Lb,只有两指针同时存在时,才需要讨论
? ? while(pa && pb){
? ? ? ? x = pa->expn-pb->expn;
? ? ? ? //判断pa 所指结点的指数与pb 所指结点指数的大小关系
? ? ? ? if(x<0){
? ? ? ? ? ? //如果小,则找去 qa 结点到Lc 上
? ? ? ? ? ? pc = pa;
? ? ? ? ? ? len++;
? ? ? ? ? ? pa = pa->next;
? ? ? ? }
? ? ? ? //如果相等,则判断两结点的系数和是否为0
? ? ? ? else if(x == 0){
? ? ? ? ? ? // 请在下面的Begin-End之间补充代码,完成一元多项式的相加。
? ? ? ? ? ? /********** Begin *********/
y = pa-> coef +pb->coef;
if(y != 0)
{pa -> coef =y;
pc = pa;
len++;
}else{
pc ->next = pa->next;
free(pa);
? ? ? ? }
pa=pc ->next;
u= pb;
pb=pb->next;
free(u);
? ?
? ? ? ? ? ? /********** End **********/
? ? ? ? }
? ? ? ? //如果pb 所指结点指数值小,则摘取pb所指结点到 LC链表上
? ? ? ? else{
? ? ? ? ? ? u = pb->next;
? ? ? ? ? ? pb->next= pa;
? ? ? ? ? ? pc->next=pb;
? ? ? ? ? ? pc = pb;
? ? ? ? ? ? len++;
? ? ? ? ? ? pb = u;
? ? ? ? }
? ? }
? ? //由于是在 La 上进行一元多项式的加和,所以如果运行过程 pa 不再有结点,而pb 上有,则需要将pb剩余结点链接到 Lc 上
? ? if(pb){
? ? ? ? pc->next = pb;
? ? }
? ? //计算 Lc 的长度
? ? while(pc){
? ? ? ? pc = pc->next;
? ? ? ? if(pc){
? ? ? ? ? ? len++;
? ? ? ? }
? ? }
? ? //Lc 的头结点中记录Lc 链表的长度
? ? Lc->coef = len;
? ? //加和完成的同时,释放Lb 结点
? ? free(Lb);
? ? return Lc;
}
//根据链表存储信息。输出结点 q
void printpoly(PLinkList q){
? ? if(q->expn == 0){
? ? ? ? printf("%.0f",q->coef);
? ? }
? ? else if(q->expn == 1){
? ? ? ? if(q->coef == 1){
? ? ? ? ? ? printf("x");
? ? ? ? }
? ? ? ? else if (q->coef == -1){
? ? ? ? ? ? printf("-x");
? ? ? ? }
? ? ? ? else{
? ? ? ? ? ? printf("%.0f",q->coef);
? ? ? ? ? ? printf("x");
? ? ? ? }
? ? }
? ? else if (q->coef == 1){
? ? ? ? printf("x^%d",q->expn);
? ? }
? ? else if(q->coef == -1){
? ? ? ? printf("-x^%d",q->expn);
? ? }
? ? else{
? ? ? ? printf("%.0fx^%d",q->coef,q->expn);
? ? }
}
//输出一元多项式L
void printpolyn(PLinkList L){
? ? int n;
? ? PLinkList p;
? ? p = L->next;
? ? n = 0;
? ? while(p){
? ? ? ? n++;
? ? ? ? if(n == 1){
? ? ? ? ? ? printpoly(p);
? ? ? ? }else if(p->coef>0){
? ? ? ? ? ? printf("+");
? ? ? ? ? ? printpoly(p);
? ? ? ? }else{
? ? ? ? ? ? printpoly(p);
? ? ? ? }
? ? ? ? p = p->next;
? ? }
}
int main(){
? ? PLinkList La,Lb,Lc;
? ? int m,n;
? ? //根据 n 的值,创建链表La
? ? scanf("%d",&n);
? ? La = (PLinkList)malloc(sizeof(PLnode));
? ? creatpolyn(La,n);
? ? //根据 m 的值,创建 Lb
? ? scanf("%d",&m);
? ? Lb = (PLinkList)malloc(sizeof(PLnode));
? ? creatpolyn(Lb,m);
? ? //输出La和Lb
? ? printf("La=");
? ? printpolyn(La);
? ? printf("\nLb=");
? ? printpolyn(Lb);
? ? //计算La+Lb,结果保存在 Lc中
? ? printf("\n计算结果为:");
? ? Lc = addpolyn(La,Lb);
? ? printf("\nLc=");
? ? printpolyn(Lc);
? ? return 0;
}
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!