代码随想录算法训练营第50天| 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
JAVA代码编写
123.买卖股票的最佳时机III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1]
输出:0
提示:
1 <= prices.length <= 1050 <= prices[i] <= 105
方法一:动态规划
思路:
关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。
接来下我用动态规划五部曲详细分析一下:
1.确定dp数组以及下标的含义
一天一共就有五个状态,
| 0 | 没有操作 (其实我们也可以不设置这个状态) |
|---|---|
| 1 | 第一次持有股票 |
| 2 | 第一次不持有股票 |
| 3 | 第二次持有股票 |
| 4 | 第二次不持有股票 |
dp[i] [j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i] [j]表示第i天状态j所剩最大现金。
需要注意:dp[i] [1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区。
例如 dp[i] [1] ,并不是说 第i天一定买入股票,有可能 第 i-1天 就买入了,那么 dp[i] [1] 延续买入股票的这个状态。
2.确定递推公式
达到dp[i] [1]状态,有两个具体操作:
- 操作一:第i天买入股票了,那么dp[i] [1] = dp[i-1] [0] - prices[i]
- 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i] [1] = dp[i - 1] [1]
那么dp[i] [1]究竟选 dp[i-1] [0] - prices[i],还是dp[i - 1] [1]呢?
一定是选最大的,所以 dp[i] [1] = max(dp[i-1] [0] - prices[i], dp[i - 1] [1]);
同理dp[i] [2]也有两个操作:
- 操作一:第i天卖出股票了,那么dp[i] [2] = dp[i - 1] [1] + prices[i]
- 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i] [2] = dp[i - 1] [2]
所以dp[i] [2] = max(dp[i - 1] [1] + prices[i], dp[i - 1] [2])
同理可推出剩下状态部分:
dp[i] [3] = max(dp[i - 1] [3], dp[i - 1] [2] - prices[i]);
dp[i] [4] = max(dp[i - 1] [4], dp[i - 1] [3] + prices[i]);
3.dp数组如何初始化
第0天没有操作,这个最容易想到,就是0,即:dp[0] [0] = 0;
第0天做第一次买入的操作,dp[0] [1] = -prices[0];
第0天做第一次卖出的操作,这个初始值应该是多少呢?
此时还没有买入,怎么就卖出呢? 其实大家可以理解当天买入,当天卖出,所以dp[0] [2] = 0;
第0天第二次买入操作,初始值应该是多少呢?应该不少同学疑惑,第一次还没买入呢,怎么初始化第二次买入呢?
第二次买入依赖于第一次卖出的状态,其实相当于第0天第一次买入了,第一次卖出了,然后再买入一次(第二次买入),那么现在手头上没有现金,只要买入,现金就做相应的减少。
所以第二次买入操作,初始化为:dp[0] [3] = -prices[0];
同理第二次卖出初始化dp[0] [4] = 0;
4.确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
5.举例推导dp数组
以输入[1,2,3,4,5]为例
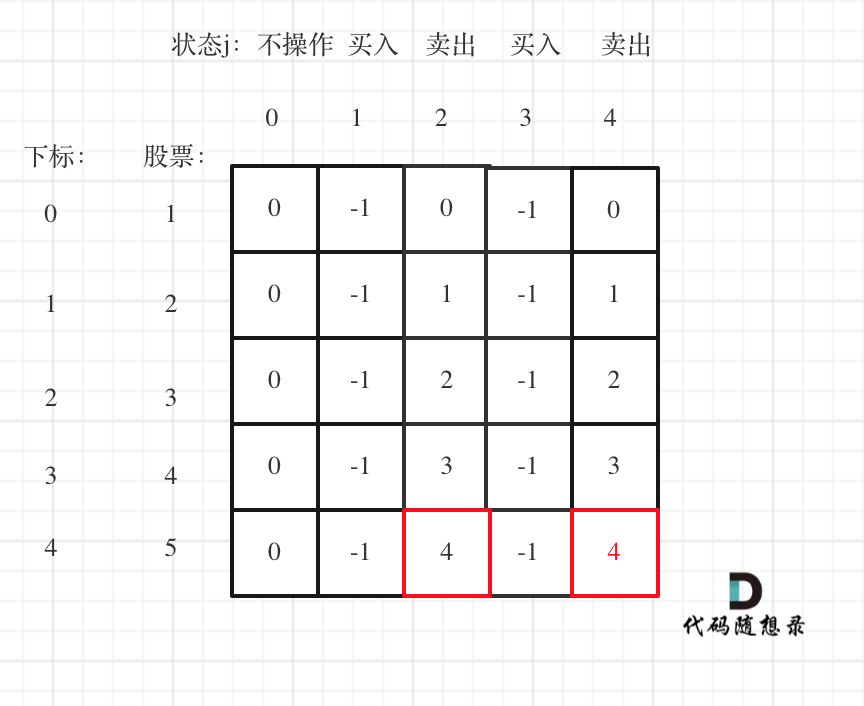
复杂度分析:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
// 边界判断, 题目中 length >= 1, 所以可省去
if (prices.length == 0) return 0;
/*
* 定义 5 种状态:
* 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出
*/
int[][] dp = new int[len][5];
dp[0][1] = -prices[0];
// 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润
dp[0][3] = -prices[0];
for (int i = 1; i < len; i++) {
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[len - 1] [4];
}
}
188.买卖股票的最佳时机IV
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
方法一:动态规划
**思路:**在123.买卖股票的最佳时机III的基础上,增加了进行k笔交易的限制
1.定义数组
一天一共就有五个状态,
| 0 | 没有操作 (其实我们也可以不设置这个状态) |
|---|---|
| 1 | 第一次持有股票 |
| 2 | 第一次不持有股票 |
| 3 | 第二次持有股票 |
| 4 | 第二次不持有股票 |
| … | |
| 2k-1 | 第k次持有股票 |
| 2k | 第k次不持有股票 |
dp[i] [j]中 i表示第i天,j为 [0 - 2k] (2k+1)个状态,dp[i] [j]表示第i天状态j所剩最大现金。
需要注意:dp[i] [1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区。
例如 dp[i] [1] ,并不是说 第i天一定买入股票,有可能 第 i-1天 就买入了,那么 dp[i] [1] 延续买入股票的这个状态。
2.确定递推公式
达到dp[i] [1]状态,有两个具体操作:
- 操作一:第i天买入股票了,那么dp[i] [1] = dp[i-1] [0] - prices[i]
- 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i] [1] = dp[i - 1] [1]
那么dp[i] [1]究竟选 dp[i-1] [0] - prices[i],还是dp[i - 1] [1]呢?
一定是选最大的,所以 dp[i] [1] = max(dp[i-1] [0] - prices[i], dp[i - 1] [1]);
同理dp[i] [2]也有两个操作:
- 操作一:第i天卖出股票了,那么dp[i] [2] = dp[i - 1] [1] + prices[i]
- 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i] [2] = dp[i - 1] [2]
所以dp[i] [2] = max(dp[i - 1] [1] + prices[i], dp[i - 1] [2])
同理可推出剩下状态部分:
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
3.dp数组如何初始化
第0天没有操作,这个最容易想到,就是0,即:dp[0] [0] = 0;
第0天做第一次买入的操作,dp[0] [1] = -prices[0];
所以同理可以推出dp[0] [j]当j为奇数的时候都初始化为 -prices[0]
代码如下:
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
在初始化的地方同样要类比j为偶数是卖、奇数是买的状态。
4.确定遍历顺序:从前向后遍历
5.举例推导dp数组
以输入[1,2,3,4,5],k=2为例。
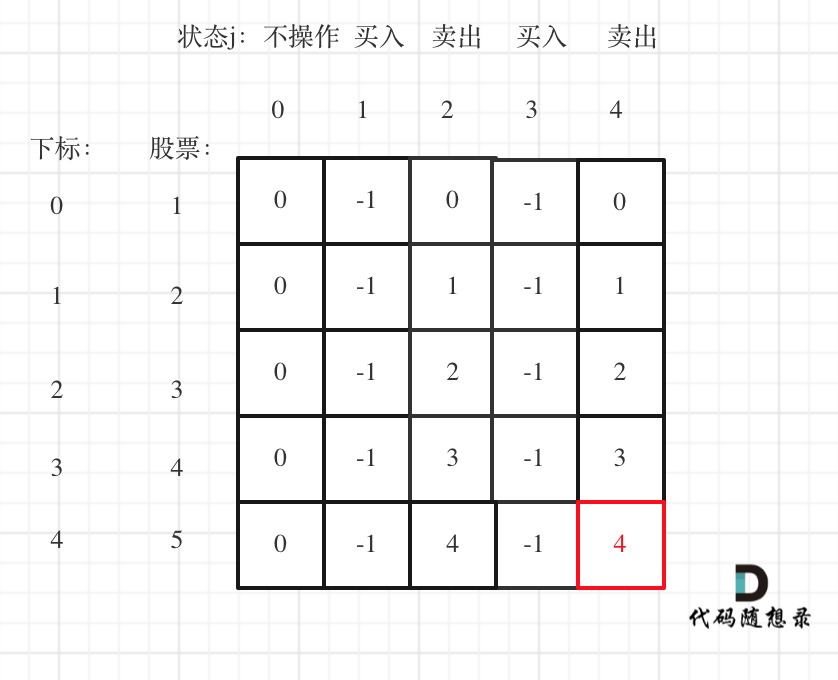
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)
- 空间复杂度:O(n)
class Solution {
public int maxProfit(int k, int[] prices) {
if (prices.length == 0) return 0;
// [天数][股票状态]
// 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作
int len = prices.length;
int[][] dp = new int[len][k*2 + 1];
// dp数组的初始化, 与版本一同理
for (int i = 1; i < k*2; i += 2) {
dp[0][i] = -prices[0];
}
for (int i = 1; i < len; i++) {
for (int j = 0; j < k*2 - 1; j += 2) {
dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[len - 1][k*2];
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!