Matlab:遗传算法,模拟退火算法练习题
2024-01-10 09:30:30
1、遗传算法
(1)遗传算法是一种基于自然选择原理和自然遗传机 制的搜索(寻优)算法,它是模拟自然界中的生命进化机制,在人工系统中实现特定目 标的优化。遗传算法的实质是通过群体搜索技术,根据适者生存的原则逐代进化,最终 得到最优解或准最优解。它必须做以下操作:初始群体的产生、求每一个体的适应度、 根据适者生存的原则选择优良个体、被选出的优良个体两两配对,通过随机交叉其染色 体的基因并随机变异某些染色体的基因后生成下一代群体,按此方法使群体逐代进化, 直到满足进化终止条件。其实现方法如下:
【1】根据具体问题确定可行解域,确定一种编码方法,能用数值串或字符串表示
可行解域的每一解。
【2】对每一解应有一个度量好坏的依据,它用一函数表示,叫做适应度函数。
【3】确定进化参数群体规模
M
、交叉概率
p
c
、变异概率
p
m
、进化终止条件。
为便于计算,一般来说,每一代群体的个体数目都取相等。群体规模越大、越容
易找到最优解,但由于受到计算机的运算能力的限制,群体规模越大,计算所需要的时
间也相应的增加。进化终止条件指的是当进化到什么时候结束,它可以设定到某一代进
化结束,也可以根据找出近似最优是否满足精度要求来确定。表
2
列出了生物遗传概念
在遗传算法中的对应关系。
(2)例:已知100个目标的经纬度,我方有一个基地,经度和纬度为(70,40)。假设我方飞机的速度为 1000 公里/小时。 我方派一架飞机从基地出发,侦察完所有目标,再返回原基地。在每一目标的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
tic
clc,clear
load sj.txt %加载100个目标的数据
x=sj(:,1:2:8); x=x(:);
y=sj(:,2:2:8); y=y(:);
sj=[x y]; d1=[70,40];
sj0=[d1;sj;d1]; sj=sj0*pi/180;
d=zeros(102); %距离矩阵d
for i=1:101
for j=i+1:102
temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
d(i,j)=6370*acos(temp);
end
end
d=d+d';L=102;w=50;dai=100;
%通过改良圈算法选取优良父代A
for k=1:w
c=randperm(100);
c1=[1,c+1,102];
flag=1;
while flag>0
flag=0;
for m=1:L-3
for n=m+2:L-1
if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
flag=1;
c1(m+1:n)=c1(n:-1:m+1);
end
end
end
end
J(k,c1)=1:102;
end
J=J/102;
J(:,1)=0;J(:,102)=1;
rand('state',sum(clock));
%遗传算法实现过程
A=J;
for k=1:dai %产生0~1间随机数列进行编码
B=A;
c=randperm(w);
%交配产生子代B
for i=1:2:w
F=2+floor(100*rand(1));
temp=B(c(i),F:102);
B(c(i),F:102)=B(c(i+1),F:102);
B(c(i+1),F:102)=temp;
end
%变异产生子代C
by=find(rand(1,w)<0.1);
if length(by)==0
by=floor(w*rand(1))+1;
end
C=A(by,:);
L3=length(by);
for j=1:L3
bw=2+floor(100*rand(1,3));
bw=sort(bw);
C(j,:)=C(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]);
end
G=[A;B;C];
TL=size(G,1);
%在父代和子代中选择优良品种作为新的父代
[dd,IX]=sort(G,2);temp(1:TL)=0;
for j=1:TL
for i=1:101
temp(j)=temp(j)+d(IX(j,i),IX(j,i+1));
end
end
[DZ,IZ]=sort(temp);
A=G(IZ(1:w),:);
end
path=IX(IZ(1),:)
long=DZ(1)
toc
xx=sj0(path,1);yy=sj0(path,2);
plot(xx,yy,'-o')
2、模拟退火算法
(1)模拟退火算法得益于材料的统计力学的研究成果。统计力学表明材料中粒子的不 同结构对应于粒子的不同能量水平。在高温条件下,粒子的能量较高,可以自由运动和 重新排列。在低温条件下,粒子能量较低。如果从高温开始,非常缓慢地降温(这个过 程被称为退火),粒子就可以在每个温度下达到热平衡。当系统完全被冷却时,最终形成处于低能状态的晶体。
(2)例:已知100个目标的经纬度,我方有一个基地,经度和纬度为(70,40)。假设我方飞机的速度为 1000 公里/小时。 我方派一架飞机从基地出发,侦察完所有目标,再返回原基地。在每一目标的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
tic
clc,clear
load sj.txt %加载100个目标的数据
x=sj(:,1:2:8);
x=x(:);
y=sj(:,2:2:8);
y=y(:);
sj=[x y];
d1=[70,40];
sj=[d1;sj;d1];
sj=sj*pi/180;
d=zeros(102); %距离矩阵d
for i=1:101
for j=i+1:102
temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
d(i,j)=6370*acos(temp);
end
end
d=d+d';
S0=[];Sum=inf;
rand('state',sum(clock));
for j=1:1000
S=[1 1+randperm(100),102];
temp=0;
for i=1:101
temp=temp+d(S(i),S(i+1));
end
if temp<Sum
S0=S;Sum=temp;
end
end
e=0.1^30;L=20000;at=0.999;T=1;
%退火过程
for k=1:L
%产生新解
c=2+floor(100*rand(1,2));
c=sort(c);
c1=c(1);
c2=c(2);
%计算代价函数值
df=d(S0(c1-1),S0(c2))+d(S0(c1),S0(c2+1))-d(S0(c1-1),S0(c1))-d(S0(c2),S0(c2+1));
%接受准则
if df<0
S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)];
Sum=Sum+df;
elseif exp(-df/T)>rand(1)
S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)];
Sum=Sum+df;
end
T=T*at;
if T<e
break;
end
end
%输出巡航路径及路径长度
S0,Sum
toc
xx=sj(S0,1);
yy=sj(S0,2);
plot(xx,yy,'-*')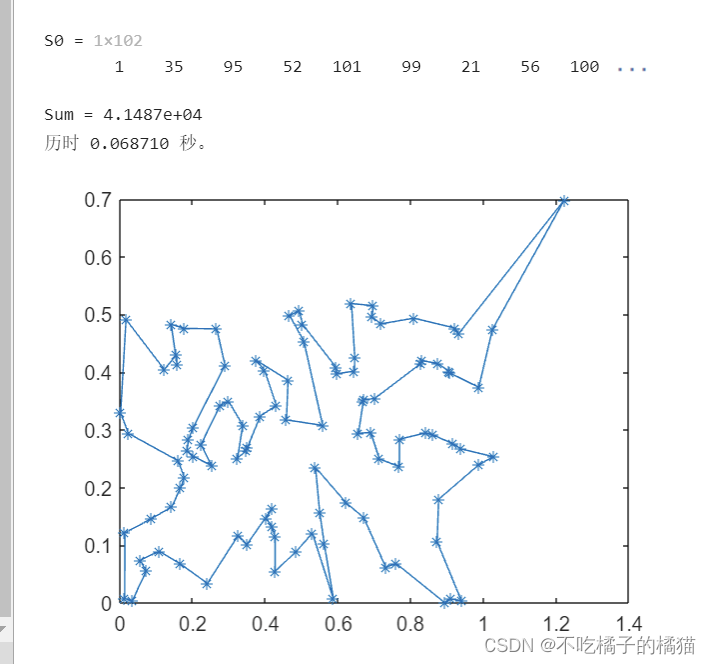
文章来源:https://blog.csdn.net/weixin_73011353/article/details/135429479
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!