【笔记】左偏树

---

算法进阶课整理

CSDN个人主页：更好的阅读体验

左偏树功能简介

左偏树本质上是一个二叉堆，支持 $O(1)$ 求最值，$O(\log n)$ 删除最值。

不过由于它还支持 $O(\log n)$ 合并两个二叉堆，所以一般左偏树相关的题目都是若干棵左偏树构成森林。

定义与一些性质

左偏树中每个节点维护两个值，点权 $v$ 和与最近空节点的距离 $dist$。

点权 $v$ 满足堆性质，即当前点点权小于任意一个儿子的点权。这种二叉堆我们一般称为“小根堆”。同样的，大根堆中当前点点权大于任意一个儿子的点权。为了方便，本篇文章主要探究小根堆的性质。

与最近空节点的距离 $dist$ 满足：

1. 叶子节点的 $dist=1$；
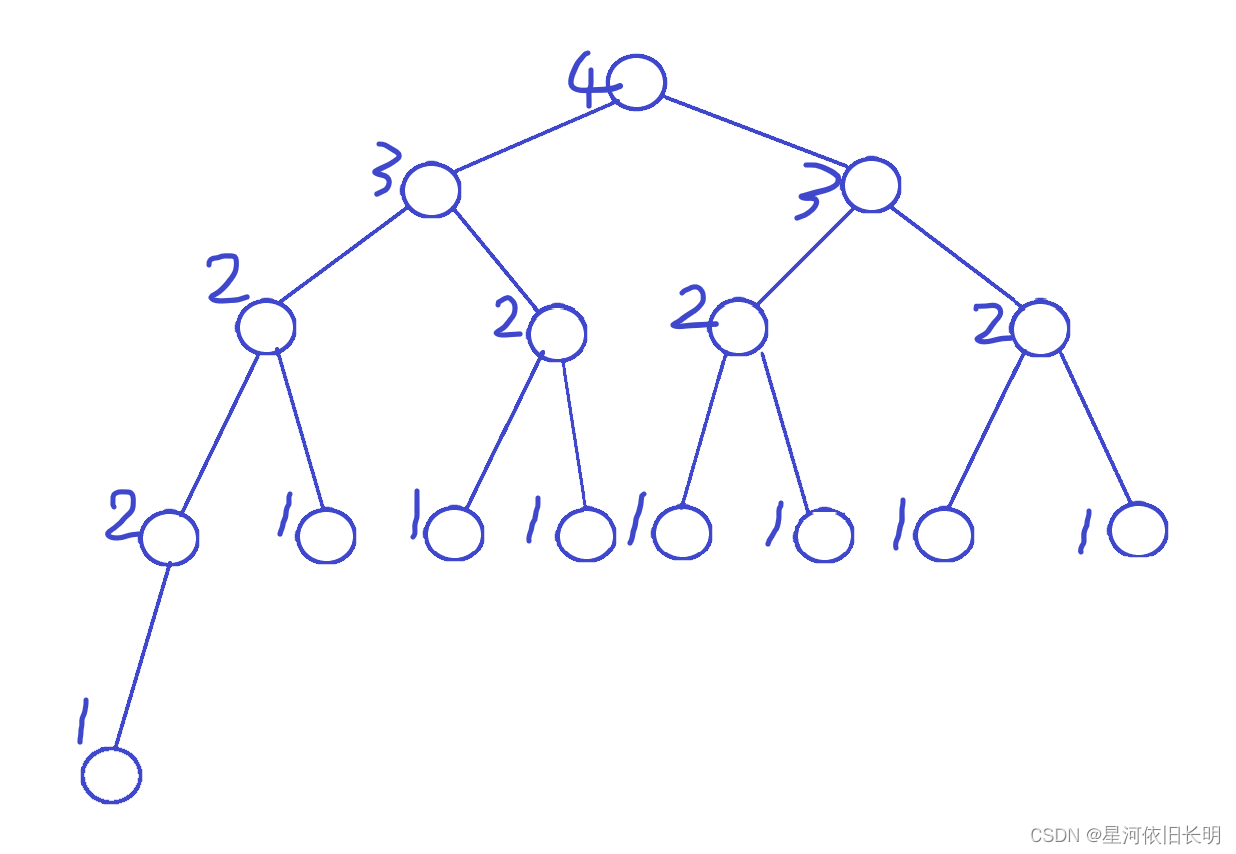
2. 每个节点左儿子的 $dist$ 都大于等于右儿子的 $dist$。这就会导致整棵树是一个向左偏的形状，因此被称为左偏树。

因此，每个节点的 $dist$ 都是右儿子的 $dist+1$。

下图就是一棵左偏树。

一棵有 $n$ 个节点的左偏树，根的 $dist\le {\log }_2(n+1)$，因为一棵根的 $dist$ 为 $x$ 的二叉树至少有 $x?1$ 层是满二叉树，那么就至少有 $2^x?1$ 个节点。

由于左偏树的时间复杂度与 $dist$ 正相关，所以左偏树操作的复杂度也为 $O(\log n)$。

---

核心操作：合并

算法流程

1. 比较两棵左偏树 $x,y$ 根节点点权的大小。不妨设 $v_{\text{root}x}\le v_{\text{root}y}$（如果不满足的话交换 $x,y$ 即可）。
2. 易证 $?u\in y,v_u\ge v_{\text{root}x}$。因此将 $\text{root}x$ 作为合并后的左偏树的根节点是合法的。
3. 由于堆没有限制左右儿子点权的关系，所以 $x$ 左子树也不需要改变，$y$ 直接递归地合并到 $x$ 的右子树即可。
4. 合并结束后，右子树的 $dist$ 会改变，因此如果此时不满足左偏树性质，交换当前节点的左右儿子即可。

时间复杂度

由于每次合并会向下跳一级，所以最多跳 $dis{t}_x+dis{t}_y$ 次就会跳到空节点。

而 $dis{t}_x,dis{t}_y\le {\log }_{2}n$，因此合并的时间复杂度为 $O(\log n)$。

代码

int merge(int x, int y)
{
    if (!x || !y) return x + y; // 如果左右子树有一个为空就返回那个非空的
    if (cmp(y, x)) swap(x, y); // 保证dist较大的在左边
    tr[x].r = merge(tr[x].r, y); // 递归，将dist较小的向左合并
    if (tr[tr[x].l].dist < tr[tr[x].r].dist) swap(tr[x].l, tr[x].r);
    // 如果合并之后不满足左偏性质就交换左右子树
    tr[x].dist = tr[tr[x].r].dist + 1;
    // 更新当前节点dist为右子树dist+1
    return x; // 返回合并之后根节点编号
}

---

其他的操作

插入

算法流程

插入操作没有专门的做法，我们考虑新建一个仅含有要插入节点的左偏树，将其合并到想要合并的树中即可。

时间复杂度 $O(\log n)$

找最值

算法流程

输出相应左偏树顶的点权即可。

时间复杂度 $O(1)$

删除最值

算法流程

由于最值为这个左偏树根节点的点权，因此删去这个点之后根节点就被删掉了。此时考虑合并根节点的左右子树即可。

时间复杂度 $O(\log n)$

---

例题 $1$：AcWing 2714. 左偏树

原题链接

题目描述

你需要维护一个小根堆的集合，初始时集合是空的。

该集合需要支持如下四种操作：

1. 1 a，在集合中插入一个新堆，堆中只包含一个数 $a$。
2. 2 x y，将第 $x$ 个插入的数和第 $y$ 个插入的数所在的小根堆合并。数据保证两个数均未被删除。若两数已在同一堆中，则忽略此操作。
3. 3 x，输出第 $x$ 个插入的数所在小根堆的最小值。数据保证该数未被删除。
4. 4 x，删除第 $x$ 个插入的数所在小根堆的最小值（若最小值不唯一，则优先删除先插入的数）。数据保证该数未被删除。

输入格式

第一行包含整数 $n$，表示总操作数量。

接下来 $n$ 行，每行包含一个操作命令，形式如题所述。

输出格式

对于每个操作 $3$，输出一个整数，占一行，表示答案。

数据范围

$1\le n\le 2\times 10^5$,
$1\le a\le 10^9$,
$1\le x,y\le$ 当前插入数的个数。
数据保证所有操作合法。

思路

发现题目输入的是第 $x$ 个加入的数，并且还需要维护连通性，因此考虑并查集。

使用并查集维护连通块，连通块的根节点就是对应的左偏树的根节点。这样能快速地找到每个节点对应的根节点编号。

• 操作 $1$：按加入的顺序分配编号即可。
• 操作 $2$：如果两个点不在同一个连通块内，就合并两个左偏树，同时合并两个连通块。
• 操作 $3$：直接输出根节点值即可。
• 操作 $4$：左偏树的删除操作较好实现，不过并查集一般难以实现删除操作，于是考虑换根。由于我们删除的肯定是根节点，而根节点的父亲指针指向自身，所以考虑将根节点父指针指向合并后的新根。同时，新根的父指针指向自己。这样就维护了新根节点的信息。至于还在连通块中的那个应该被删除的节点，反正遍历不到，就不用管了。

---

代码

#include <iostream>

using namespace std;

const int N = 200010;

struct Leftist_Tree_Node
{ // 定义左偏树节点
    int l, r; // 左右儿子
    int v, dist; // 点权、距离
    void init(int _v)
    {
        v = _v, dist = 1;
    }
}tr[N];

int n, idx; // idx时间戳，记录插入点的顺序
int p[N]; // 并查集父指针

int find(int x) // 并查集
{
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

inline bool cmp(int x, int y) // 比较两个点点权，如果x的点权较小就返回1，否则返回0
{
    if (tr[x].v != tr[y].v) return tr[x].v < tr[y].v;
    return x < y; // 题目要求先删早加入的点
}

int merge(int x, int y) // 合并
{
    if (!x || !y) return x + y;
    if (cmp(y, x)) swap(x, y);
    tr[x].r = merge(tr[x].r, y);
    if (tr[tr[x].l].dist < tr[tr[x].r].dist) swap(tr[x].l, tr[x].r);
    tr[x].dist = tr[tr[x].r].dist + 1;
    return x;
}

int main()
{
    int op, x, y;
    scanf("%d", &n);
    tr[0].init(1e9); // 处理边界情况
    while (n -- )
    {
        scanf("%d%d", &op, &x);
        if (op == 1)
        {
            tr[ ++ idx].init(x); // 新建节点，分配编号
            p[idx] = idx; // 初始化并查集
        }
        else if (op == 2)
        {
            scanf("%d", &y);
            int r1 = find(x), r2 = find(y); // 找到两个根节点
            if (r1 != r2) // 如果不在一个连通块内
            {
                if (cmp(r2, r1)) swap(r1, r2); // 比大小，将点权小的放前面
                merge(r1, r2); // 左偏树合并
                p[r2] = r1; // 连通块合并
            }
        }
        else if (op == 3) printf("%d\n", tr[find(x)].v); // x所在连通块根节点的权值
        else
        {
            int rt = find(x);
            if (cmp(tr[rt].r, tr[rt].l)) swap(tr[rt].l, tr[rt].r); // 交换
            merge(tr[rt].l, tr[rt].r); // 合并左右子树，即删除根节点
            p[rt] = tr[rt].l, p[tr[rt].l] = tr[rt].l; // 并查集换根
        }
    }

    return 0;
}

---

例题 $2$：洛谷 P3377 【模板】左偏树/可并堆

原题链接

题目描述

如题，一开始有 $n$ 个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

1. 1 x y：将第 $x$ 个数和第 $y$ 个数所在的小根堆合并（若第 $x$ 或第 $y$ 个数已经被删除或第 $x$ 和第 $y$ 个数在用一个堆内，则无视此操作）。

2. 2 x：输出第 $x$ 个数所在的堆最小数，并将这个最小数删除（若有多个最小数，优先删除先输入的；若第 $x$ 个数已经被删除，则输出 $?1$ 并无视删除操作）。

输入格式

第一行包含两个正整数 $n,m$，分别表示一开始小根堆的个数和接下来操作的个数。

第二行包含 $n$ 个正整数，其中第 $i$ 个正整数表示第 $i$ 个小根堆初始时包含且仅包含的数。

接下来 $m$ 行每行 $2$ 个或 $3$ 个正整数，表示一条操作，格式如下：

操作 $1$：1 x y

操作 $2$：2 x

输出格式

输出包含若干行整数，分别依次对应每一个操作 $2$ 所得的结果。

数据范围

对于 $30\%$ 的数据：$n\le 10$，$m\le 10$。
对于 $70\%$ 的数据：$n\le 10^3$，$m\le 10^3$。
对于 $100\%$ 的数据：$n\le 10^5$，$m\le 10^5$，初始时小根堆中的所有数都在 int 范围内。

---

思路

本题与上题大致相同，但需要手动判断一个数是否已经被删除。由于并查集不能删除元素，所以考虑为每个节点维护一个标记表示是否被删除。

注意读题。

将 这个最小数 删除（若有多个最小数，优先删除先输入的；若 第 $x$ 个数 已经被删除，则输出 $?1$ 并无视删除操作）。

具体细节见代码。

代码

#include <iostream>

using namespace std;

const int N = 100010;

struct Leftist_Tree_Node
{
	int l, r;
	int v, dist;
	void init(int _v)
	{
		v = _v, dist = 1;
	}
}tr[N];

int n, m;
int p[N];
bool st[N]; // 如果已经被删除，则为 true

int find(int x)
{
	if (x != p[x]) p[x] = find(p[x]);
	return p[x];
}

inline bool cmp(int x, int y)
{
	if (tr[x].v != tr[y].v) return tr[x].v < tr[y].v;
	return x < y;
}

int merge(int x, int y)
{
	if (!x || !y) return x + y;
	if (cmp(y, x)) swap(x, y);
	tr[x].r = merge(tr[x].r, y);
	if (tr[tr[x].l].dist < tr[tr[x].r].dist) swap(tr[x].l, tr[x].r);
	tr[x].dist = tr[tr[x].r].dist + 1;
	return x;
}

int main()
{
	int op, x, y;
	tr[0].init(2e9);
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++ )
	{
		scanf("%d", &x);
		tr[i].init(x), p[i] = i;
	}

	while (m -- )
	{
		scanf("%d%d", &op, &x);
		if (op == 1)
		{
			scanf("%d", &y);
			int r1 = find(x), r2 = find(y);
			if (st[x] || st[y] || r1 == r2) continue;
			// 注意 st 里是原数据而不是并查集根节点
			if (cmp(r2, r1)) swap(r1, r2);
			p[r2] = r1;
			merge(r1, r2);
		}
		else
		{
			int rt = find(x);
			if (st[x]) puts("-1");
			// 注意读题。当前点已经被删除输出-1.
			else
			{
				printf("%d\n", tr[rt].v);
				if (cmp(tr[rt].r, tr[rt].l)) swap(tr[rt].l, tr[rt].r);
				merge(tr[rt].l, tr[rt].r);
				st[rt] = true; // 注意读题。删除最小数，即删除根节点。
				p[rt] = tr[rt].l, p[tr[rt].l] = tr[rt].l;
			}
		}
	}
	return 0;
}

---

最后，如果觉得对您有帮助的话，点个赞再走吧！