C++迷宫问题完全详解

一、提出问题

迷宫我们都玩过，有些复杂的看的眼花缭乱，但是有没有想过，让机器帮你完成这个工作，想着就很酷，好，废话不多说，直接开干！！！

二、寻找解决方法

解决迷宫问题可以有多种算法，这里介绍深度优先搜索跟广度优先算法。
深度优先搜索（DFS）和广度优先搜索（BFS）是两种常用的图遍历算法，适用于不同的问题和场景。下面我将对它们进行解释，并介绍它们的适用场景以及优缺点。

深度优先搜索（DFS）：

• 深度优先搜索从起始节点开始，沿着一条路径尽可能深入地访问节点，直到无法继续或者达到目标节点为止。
• 在每个节点上，DFS首先探索一个子节点，然后再探索另一个子节点，以此类推，直到所有可能的路径都被探索完毕。
• DFS使用栈来保存需要进一步探索的节点，因此采用了后进先出（LIFO）的策略。

适用场景：

• 当问题的解决方案位于树或图的深处时，DFS通常更有效，因为它能够快速地向下搜索并深入解空间。
• 例如，在迷宫问题中，DFS可以通过在每个位置上依次探索四个方向的移动来搜索路径，直到找到终点或无法继续移动为止。

优点：

1. 实现简单，只需使用递归或堆栈即可。
2. 对于解决方案位于深处的问题，DFS通常比BFS更快。

缺点：

1. 可能陷入无限循环，如果图中存在环路。
2. 不保证找到最短路径，因为它首先遍历深度较大的节点。

广度优先搜索（BFS）：

• 广度优先搜索从起始节点开始，逐层地访问相邻节点，直到找到目标节点或者遍历完整个图。
• 在每一层上，BFS首先访问当前节点的所有未访问邻居节点，然后再依次访问下一层的节点。
• BFS使用队列来保存需要进一步探索的节点，因此采用了先进先出（FIFO）的策略。

适用场景：

• 当问题的解决方案位于树或图的较浅部分时，BFS通常更有效，因为它可以快速地扩展到距离起始节点更远的节点。
• 例如，在查找最短路径的问题中，BFS可以找到从起点到终点的最短路径。

优点：

1. 可以找到最短路径，因为它按层次遍历图。
2. 对于解决方案位于较浅部分的问题，BFS通常比DFS更快。

缺点：

1. 需要额外的空间来存储队列，可能占用较多的内存。
2. 在搜索深度较大的图时，BFS可能会变得比较慢。

总结：

• DFS适用于解决方案位于深处的问题，并且不需要找到最短路径。
• BFS适用于解决方案位于较浅部分的问题，并且需要找到最短路径。

在实际应用中，根据问题的特点和需求，选择合适的算法来进行图遍历是非常重要的。
既然两种方法都能实现，那我就两个都实现了把，广度优先算法能找到最短路径，深度优先算法能尽快找出出口，各有优点。

三、深度优先查找

3.1 深度优先实现代码

#include <iostream>
#include <stack>
#include <queue>
#include <vector>

struct Point {
	int x;
	int y;

	Point(int x, int y) : x(x), y(y) {}
};

// 检查点是否在迷宫范围内
bool isValidPoint(const std::vector<std::vector<int>>& maze, int x, int y) {
	int rows = maze.size();
	int cols = maze[0].size();

	return (x >= 0 && x < rows && y >= 0 && y < cols && maze[x][y] == 0);
}

// 解决迷宫问题-深度优先
bool solveMaze(std::vector<std::vector<int>>& maze, const Point& start, const Point& end) {
	int rows = maze.size();
	int cols = maze[0].size();

	// 创建堆栈
	std::stack<Point> stack;
	stack.push(start);

	// 创建标记矩阵，用于记录已访问的点
	std::vector<std::vector<bool>> visited(rows, std::vector<bool>(cols, false));
	visited[start.x][start.y] = true;

	// 定义四个方向上的移动
	int dx[] = { 0, 1, 0, -1 };
	int dy[] = { -1, 0, 1, 0 };

	while (!stack.empty()) {
		Point current = stack.top();

		// 如果当前点是终点，找到解决方案，返回真
		if (current.x == end.x && current.y == end.y) {
			// 标记路径上的位置为-1
			while (!stack.empty()) {
				Point point = stack.top();
				maze[point.x][point.y] = -1;
				stack.pop();
			}
			return true;
		}

		// 尝试四个方向上的移动
		bool moved = false;
		for (int i = 0; i < 4; i++) {
			int newX = current.x + dx[i];
			int newY = current.y + dy[i];

			if (isValidPoint(maze, newX, newY) && !visited[newX][newY]) {
				stack.push(Point(newX, newY));
				visited[newX][newY] = true;
				moved = true;
				break;
			}
		}

		// 如果无法移动到相邻点，则回溯到上一个点
		if (!moved) {
			stack.pop();
		}
	}

	// 没有找到解决方案，返回假
	return false;
}
// 打印迷宫图
void printMaze(const std::vector<std::vector<int>>& maze, const Point& start, const Point& end) {
	int rows = maze.size();
	int cols = maze[0].size();

	// 输出上边框
	for (int i = 0; i < cols + 2; i++) {
		std::cout << "# ";
	}
	std::cout << std::endl;

	// 输出迷宫内容
	for (int i = 0; i < rows; i++) {
		std::cout << "# "; // 左边框

		for (int j = 0; j < cols; j++) {
			if (i == start.x && j == start.y) {
				std::cout << "S "; // 起点标记为"S"
			}
			else if (i == end.x && j == end.y) {
				std::cout << "E "; // 终点标记为"E"
			}
			else if (maze[i][j] == 0) {
				std::cout << "  "; // 空路径
			}
			// 在路径上画线
			else if (maze[i][j] == -1) {
				std::cout << "x ";
			}
			else {
				std::cout << "█ "; // 墙壁
			}
		}

		std::cout << "#" << std::endl; // 右边框
	}

	// 输出下边框
	for (int i = 0; i < cols + 2; i++) {
		std::cout << "# ";
	}
	std::cout << std::endl;
}


int main() {
	std::vector<std::vector<int>> maze = {
		{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
		{ 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1 },
		{ 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1 },
		{ 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1 },
		{ 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1 },
		{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 }
	};


	Point start(1, 1);
	Point end(13, 13);

	std::cout << "初始迷宫：" << std::endl;
	printMaze(maze, start, end);

	bool isSolvable = solveMaze(maze, start, end);

	if (isSolvable) {
		std::cout << "迷宫可以解决！" << std::endl;
	}
	else {
		std::cout << "迷宫无解！" << std::endl;
	}

	std::cout << "解决后的迷宫：" << std::endl;
	printMaze(maze, start, end);
	while(1);

	return 0;
}

3.1 输出结果：

S代表起始点，E代表终点，x代表路径

3.2 原理讲解

这里使用了栈，stack是一种先进后出(First In Last Out,FILO)的数据结构，它只有一个出口

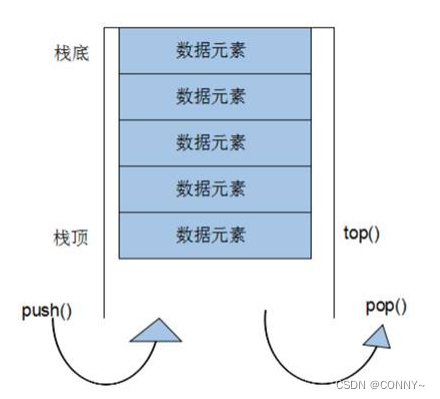
栈中只有顶端的元素才可以被外界使用，因此栈不允许有遍历行为
栈中进入数据称为 — 入栈 push
栈中弹出数据称为 — 出栈 pop
生活中的栈：

深度优先搜索（DFS）：

1. 创建一个堆栈，并将起点压入堆栈。
2. 创建一个标记矩阵，并将起点标记为已访问。
3. 循环直到堆栈为空：
   4. 取出堆栈顶部的路径。
   5. 获取该路径的最后一个点作为当前点。
   6. 如果当前点是终点，则找到了解决方案，将路径上的点标记为解决路径。
   7. 尝试当前点的四个相邻点：
   • 如果满足条件（在迷宫范围内且未被访问过），则创建新的路径并将新的点压入堆栈。
   • 将相邻点标记为已访问。
   • 退出当前循环
4. 如果堆栈为空仍未找到解决方案，则表示迷宫无解。

四、广度优先查找

4.1 广度优先实现代码

#include <iostream>
#include <queue>
#include <vector>

struct Point {
	int x;
	int y;

	Point(int x, int y) : x(x), y(y) {}
};

// 检查点是否在迷宫范围内
bool isValidPoint(const std::vector<std::vector<int>>& maze, int x, int y) {
	int rows = maze.size();
	int cols = maze[0].size();

	return (x >= 0 && x < rows && y >= 0 && y < cols && maze[x][y] == 0);
}

// 解决迷宫问题并返回最短路径
std::vector<Point> solveMaze(std::vector<std::vector<int>>& maze, const Point& start, const Point& end) {
	int rows = maze.size();
	int cols = maze[0].size();

	// 创建队列
	std::queue<std::vector<Point>> queue;
	queue.push({ start });

	// 创建标记矩阵，用于记录已访问的点
	std::vector<std::vector<bool>> visited(rows, std::vector<bool>(cols, false));
	visited[start.x][start.y] = true;

	// 定义四个方向上的移动
	int dx[] = { 0, 1, 0, -1 };
	int dy[] = { -1, 0, 1, 0 };

	while (!queue.empty()) {
		std::vector<Point> path = queue.front();
		queue.pop();

		Point current = path.back();

		// 如果当前点是终点，找到解决方案，返回最短路径
		if (current.x == end.x && current.y == end.y) {
			return path;
		}

		// 尝试四个方向上的移动
		for (int i = 0; i < 4; i++) {
			int newX = current.x + dx[i];
			int newY = current.y + dy[i];

			if (isValidPoint(maze, newX, newY) && !visited[newX][newY]) {
				std::vector<Point> newPath = path;
				newPath.push_back(Point(newX, newY));
				queue.push(newPath);
				visited[newX][newY] = true;
			}
		}
	}

	// 没有找到解决方案，返回空路径表示无解
	return {};
}

// 打印迷宫图
void printMaze(const std::vector<std::vector<int>>& maze, const Point& start, const Point& end) {
	int rows = maze.size();
	int cols = maze[0].size();

	// 输出上边框
	for (int i = 0; i < cols + 2; i++) {
		std::cout << "# ";
	}
	std::cout << std::endl;

	// 输出迷宫内容
	for (int i = 0; i < rows; i++) {
		std::cout << "# "; // 左边框

		for (int j = 0; j < cols; j++) {
			if (i == start.x && j == start.y) {
				std::cout << "S "; // 起点标记为"S"
			}
			else if (i == end.x && j == end.y) {
				std::cout << "E "; // 终点标记为"E"
			}
			else if (maze[i][j] == 0) {
				std::cout << "  "; // 空路径
			}
			else if (maze[i][j] == -1) {
				std::cout << "x "; // 解决路径上的位置用"x"表示
			}
			else {
				std::cout << "█ "; // 墙壁
			}
		}

		std::cout << "#" << std::endl; // 右边框
	}

	// 输出下边框
	for (int i = 0; i < cols + 2; i++) {
		std::cout << "# ";
	}
	std::cout << std::endl;
}

int main() {
	std::vector<std::vector<int>> maze = {
		{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
		{ 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },
		{ 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1 },
		{ 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1 },
		{ 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1 },
		{ 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1 },
		{ 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 },
		{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },
		{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 }
	};

	Point start(1, 1);
	Point end(13, 13);

	std::cout << "初始迷宫：" << std::endl;
	printMaze(maze, start, end);

	std::vector<Point> shortestPath = solveMaze(maze, start, end);

	if (!shortestPath.empty()) {
		std::cout << "迷宫可以解决！最短路径长度为：" << shortestPath.size() - 1 << std::endl;

		// 标记解决路径上的位置
		for (const auto& point : shortestPath) {
			maze[point.x][point.y] = -1;
		}
	}
	else {
		std::cout << "迷宫无解！" << std::endl;
	}

	std::cout << "解决后的迷宫：" << std::endl;
	printMaze(maze, start, end);
	while (1);
	return 0;
}

4.2 输出结果

4.3 算法讲解

广度优先使用的是Queue队列，队列是一种先进先出(First In First Out,FIFO)的数据结构，它有两个出口

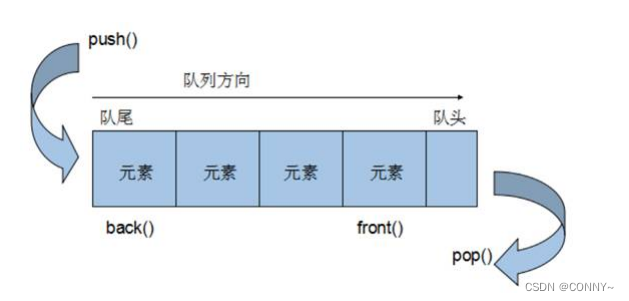
队列容器允许从一端新增元素，从另一端移除元素
队列中只有队头和队尾才可以被外界使用，因此队列不允许有遍历行为
队列中进数据称为 — 入队 push
队列中出数据称为 — 出队 pop
生活中的队列：

广度优先搜索（BFS）：

1. 创建一个队列，并将起点加入队列。
2. 创建一个标记矩阵，并将起点标记为已访问。
3. 循环直到队列为空：
   4. 从队列中取出一个路径。
   5. 获取该路径的最后一个点作为当前点。
   6. 如果当前点是终点，则找到了解决方案，返回该路径。
   7. 尝试当前点的四个相邻点：
   • 如果满足条件（在迷宫范围内且未被访问过），则创建新的路径并将新的点添加到路径中。
   • 将新的路径加入队列，并将相邻点标记为已访问。
4. 如果队列为空仍未找到解决方案，则表示迷宫无解。