D35|整数拆分+不同的二叉搜索树

96.不同的二叉搜索树

初始思路：

一开始需要推导递推公式也就是需要找规律：

我认为的规律是

dp[0] = 1;

dp[1] = 1;

dp[2] = 2;

dp[3] = dp[2]+dp[1]xdp[1]+dp[2]=5;

dp[4] = dp[3]+dp[2]xdp[1]+dp[1]xdp[2]+dp[3];

dp[5] = dp[4]+dp[1]xdp[3]+dp[2]xdp[2]+dp[3]xdp[1]+dp[4];

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        if(n<=2){return n;}
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i<n+1;i++){
            int a = i-1;
            while(a>=0){
                System.out.println("a"+a);
                dp[i]  = dp[i]+dp[a]*dp[i-1-a];
                a--;
            }
        }

        return dp[n];
    }
}

题解复盘：

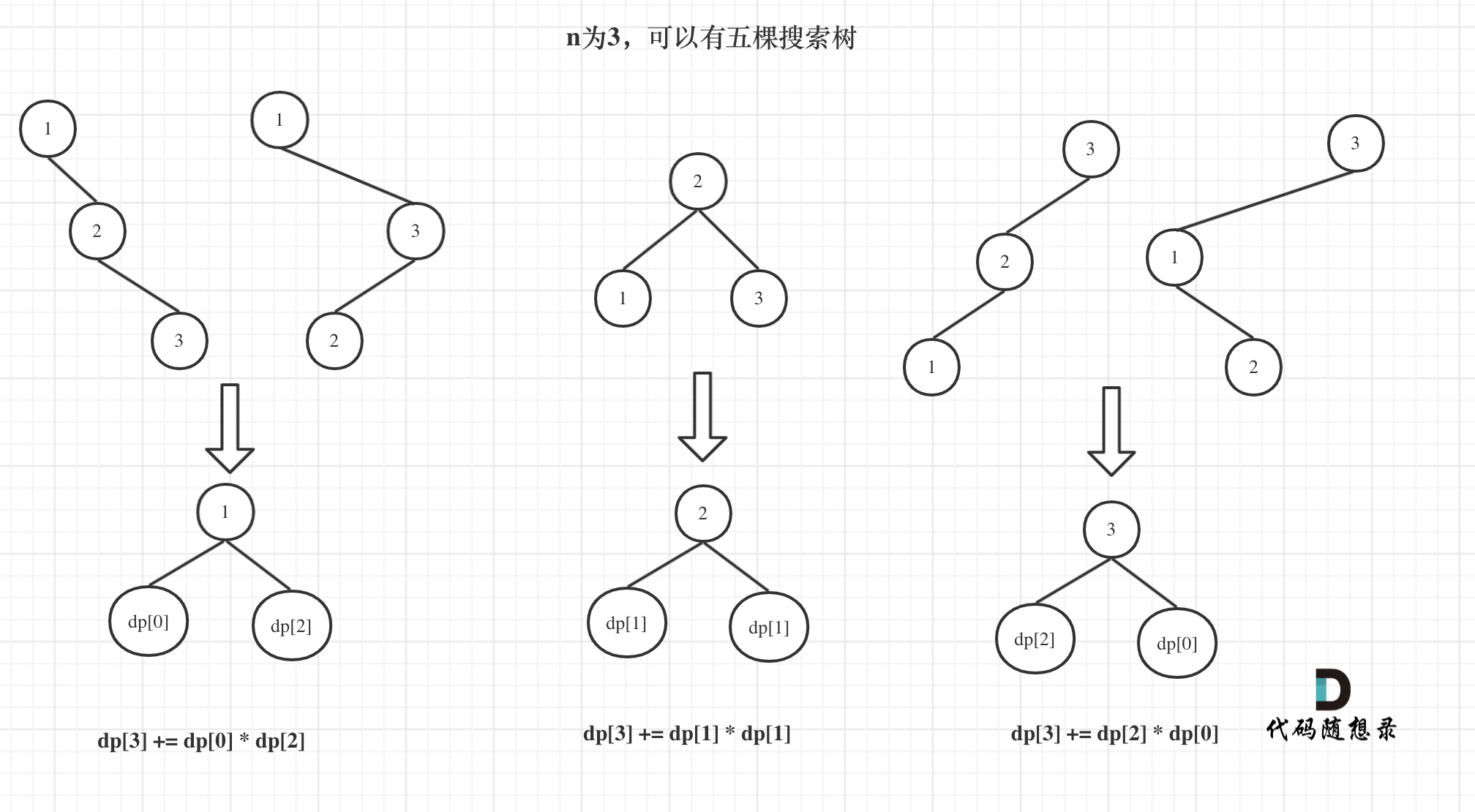
dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

如图所示：

class Solution {
    public int numTrees(int n) {
        //初始化 dp 数组
        int[] dp = new int[n + 1];
        //初始化0个节点和1个节点的情况
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

这个可能不太好想：

一共i个节点，对于根节点j时，左子树的节点个数为j-1，右子树的节点个数为i-j。

---

343.整数拆分

初始思路：

找规律，dp[i] 代表i拆分后的最大乘积

dp[2] = 1;

dp[3] = 2;

dp[4] = 4;

dp[5] = 1x4 2x3 3x2 4x1 = 6;

dp[6] = 1x5 2x4 3x3 4x2 5x1 = 9;

dp[7] = 1x6 2x5 3x4 4x3 = 12,但其实这里我们可以发现5拆为2x3x2是跟3x4的拆分结果同为最大值，也就是在拆分时2xMath.max(5,dp(5));

class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n+1];
        dp[1] = 1;
        dp[2] = 1;
        for(int i = 2;i<n+1;i++){
            for(int j = 1;j<=i/2;j++){
                dp[i] = Math.max(dp[i],Math.max(j,dp[j])*Math.max(i-j,dp[i-j]));
            }
        }
        return dp[n];
    }
}

题解复盘：

更加清晰，少了无意义的初始化

class Solution {
    public int integerBreak(int n) {
        //dp[i] 为正整数 i 拆分后的结果的最大乘积
        int[] dp = new int[n+1];
        dp[2] = 1;
        for(int i = 3; i <= n; i++) {
            for(int j = 1; j <= i-j; j++) {
                // 这里的 j 其实最大值为 i-j,再大只不过是重复而已，
                //并且，在本题中，我们分析 dp[0], dp[1]都是无意义的，
                //j 最大到 i-j,就不会用到 dp[0]与dp[1]
                dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
                // j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘
                //而j * dp[i - j]是将 i-j 拆分成两个以及两个以上的个数,再相乘。
            }
        }
        return dp[n];
    }
}j

其实不是很理解为什么不拆j。?