元旦特辑:Note5---插入排序

目录
前言🪩
Hey young fella!Welcome to my channel !我们前几篇博客学完了二叉树的一些基本内容,那么今天我们要学什么?没错👍从上次后语中,知道了我们今天要学习的是排序。本篇文章里面主要介绍插入排序的方法哦!话不多说,开始吧!
1. 排序的概念+运用🟣
1.1 排序的概念🟪
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[n]=r[m],且r[n]在r[m]之前,而在排序后的序列中,r[n]仍在r[m]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
下图是我们要学习的常见排序算法:
1.2 排序的运用💜
例如:网购的商品排序呈现、成绩排名、大学综合实力排名......

2. 直接插入排序🟢
2.1 基本思想🟩
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列?。
类似于斗地主中,拿到牌之后给自己的牌插入排序

2.2 思路分析💚

看完可视化的思路之后,相信很多小伙伴已经有了大致的思路。下面,我们来整理一下思路👇
目标:先实现升序
思路:先单趟再多趟,先局部再整体我们默认一开始前面某一部分是有序的(实际上,我们是不知道哪到哪是有序的),然后再将无序的数据开始插入进去
插入的时候会遇到以下2种情况:
情况1:该值比前面所有的数都大,那么直接接着之前的数据往后排就行
情况2: ? 该值比前面任意一个数小(这个数据不是前面有序的数据中最大的),前面比该数大的往后挪,腾出一个位置给该数插入
问题:
1. 有序的部分怎么知道?
我们假设0-end是有序的
一开始排序的时候可能只有第一个有序,那就是0-0注意??
2. 我们还需要tmp来存储end的下一个位置的数据----为什么?
情况1: ?直接在end++的位置插入数据就行
情况2: ?有一部分数据需要往后移动,end++会被覆盖掉,不保存的话,就不知道原来end++的数据是多少了
3. 循环结束的条件是什么?
2.3 代码实现?
2.3.1 sort.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//打印
void PrintArray(int* a, int n);
//直接插入排序
void InsertSort(int* a, int n);2.3.2 sort.c
#include"sort.h"
//打印
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
}
//[0,end] end+1
//直接插入排序
void InsertSort(int* a, int n)
{
//i<n-1是为了防止end+1造成数组越界
for (int i = 0; i < n - 1; i++)
{
int end=i;
int tmp = a[end + 1];
//单趟排序
while (end >= 0)//最差end走到-1,插入到最前面
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
break;
}
a[end + 1] = tmp;
}
}2.3.3 test.c

2.4 特性总结??
直接插入排序的特性总结:
1.?元素集合越接近有序,直接插入排序算法的时间效率越高
2.?时间复杂度:O(N^2)---最坏情况:逆序
3.?空间复杂度:O(1),它是一种稳定的排序算法
4.?稳定性:稳定
3. 希尔排序🟠
3.1 基本思想🟧
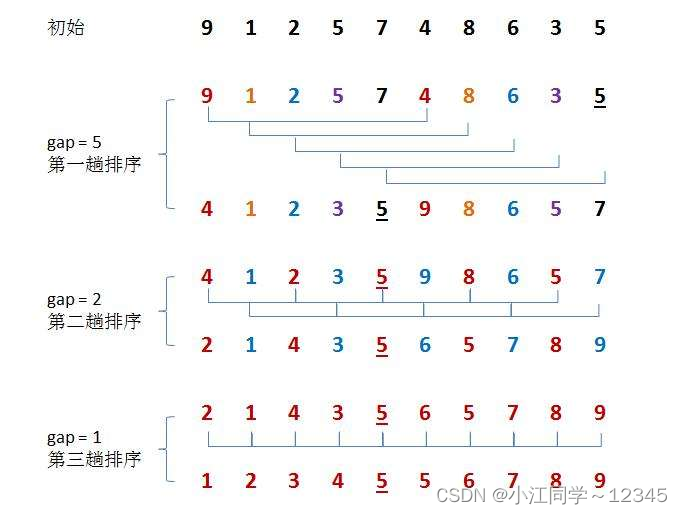
先选定一个整数---gap(我们目前还不确定gap是多少),把待排序文件中所有数据分成n/gap个组,所有距离为gap的数据分在同一组内,并对每一组内的数据进行直接插入排序。---进行预排序,使其接近有序
然后再次确定gap的值,重复上述分组和排序的工作。当最后gap=1时,(相当于直接插入排序)所有数据在统一组内排好序。
3.2 思路分析🔶
目标:实现升序
思路:先实现单趟排序,然后实现多趟排序
一、预排序:gap>1 ? 接近有序
1. 先确定gap + 分组
2. 实现单趟(一组)排序
3.实现多趟排序?
二、直接插入排序:gap==1 ? 有序
4. 所有数据进行直接插入排序
问题:
可能是后面会遇到的问题,可以和代码结合着看
1. 依据n和gap分组的时候,剩余的数据个数达不到分组的标准,出现数组越界怎么办?
3.3 预排序实现🧡
3.3.1 sort.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//打印
void PrintArray(int* a, int n);
//希尔排序
void ShellSort(int* a, int n);3.3.2 sort.c
#include"sort.h"
//打印
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
}
//希尔排序---一组一组排序
void ShellSort(int* a, int n)
{
//多趟排序
int gap = 3;
for (int j = 0; j < gap; j++)
{
//单趟排序
for (int i = j; i < n - gap; i += gap)//问题1
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
}3.3.3 优化
//希尔排序---多组并排,反复横跳
void ShellSort(int* a, int n)
{
//单趟排序
int gap = 3;
for (int i = 0; i < n - gap; i ++)//问题1
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}3.3.4?test.c
#include"sort.h"
//希尔排序
void testShellSort()
{
int a[] = { 3,2,6,8,9,7,5,10,1,4 };
int n = sizeof(a) / sizeof(int);
ShellSort(a, n);
PrintArray(a, n);
}
int main()
{
//testInsertSort();
testShellSort();
return 0;
}
3.4?完整实现??
3.4.1 gap到底设置成多少?
预排序:
1. gap过大,分组少,排序速度快,效果不好,比较不接近有序2. gap过小,分组多,排序速度慢,效果好,比较接近有序
问题来了:gap设置为多少呢?可不能是定值,数据个数不同gap定义是有差异的
注意??
gap定义的前提:我们需要保证多组预排序之后,gap==1,从而进行直接插入排序
其实,到现在并没有确切的说法说gap怎么定义是最优的,所以这里也只是一个参考:
有人觉得gap/2(可以保证最后一次的gap==1),但是还是排序太多次了,所以就提出了gap/3,但是gap/3不能保证最后一次是1(进行直接插入排序)--->gap/3+1就可以保证啦
3.4.2?sort.c
//希尔排序---多组并排,反复横跳
void ShellSort(int* a, int n)
{
int gap = n;
//预排序
while (gap > 1)
{
//单趟排序
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)//问题1
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
//直接插入排序
InsertSort(a, n);
}3.4.3?test.c

3.5 特性总结🚼
??????? 1.?希尔排序是 对直接插入排序的优化 。2.?当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3.?希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定,导致希尔排序的时间复杂度不是很好算,需要借助数学模型,感兴趣的小伙伴可以自行搜索🔍
这里,就简单说一下平均时间复杂度:O(N^1.25)-O(1.6*N^1.25)
为了方便,我们直接粗略一点:O(N^1.3)???????
4.?稳定性:不稳定
4. 性能对比--test.c🆚
// 测试排序的性能对比
// 测试排序的性能对比
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand()+i;
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
//SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
//HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
//QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
//MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
//BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort1:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BulbbleSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}
int main()
{
testInsertSort();
testShellSort();
TestOP();
return 0;
}
我们发现,希尔排序排序还是很厉害👍的
后语🪅
今天,我们学习了插入排序的实现和性能对比以及他们的特性总结。希望小伙伴们自己也可以练习一下,加强记忆和理解。
下一篇博客,我们将一起学习选择排序的相关知识点!请大家多多期待🙏
本次的分享到这里就结束了!!!
PS:小江目前只是个新手小白。欢迎大家在评论区讨论哦!有问题也可以讨论的!期待大家的互动!!!
公主/王子殿下,请给我点赞👍+收藏??+关注?(这对我真的很重要!!!)

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!