376. 摆动序列
2023-12-14 16:15:39
原题链接:
https://leetcode.cn/problems/wiggle-subsequence/description/
完成情况:
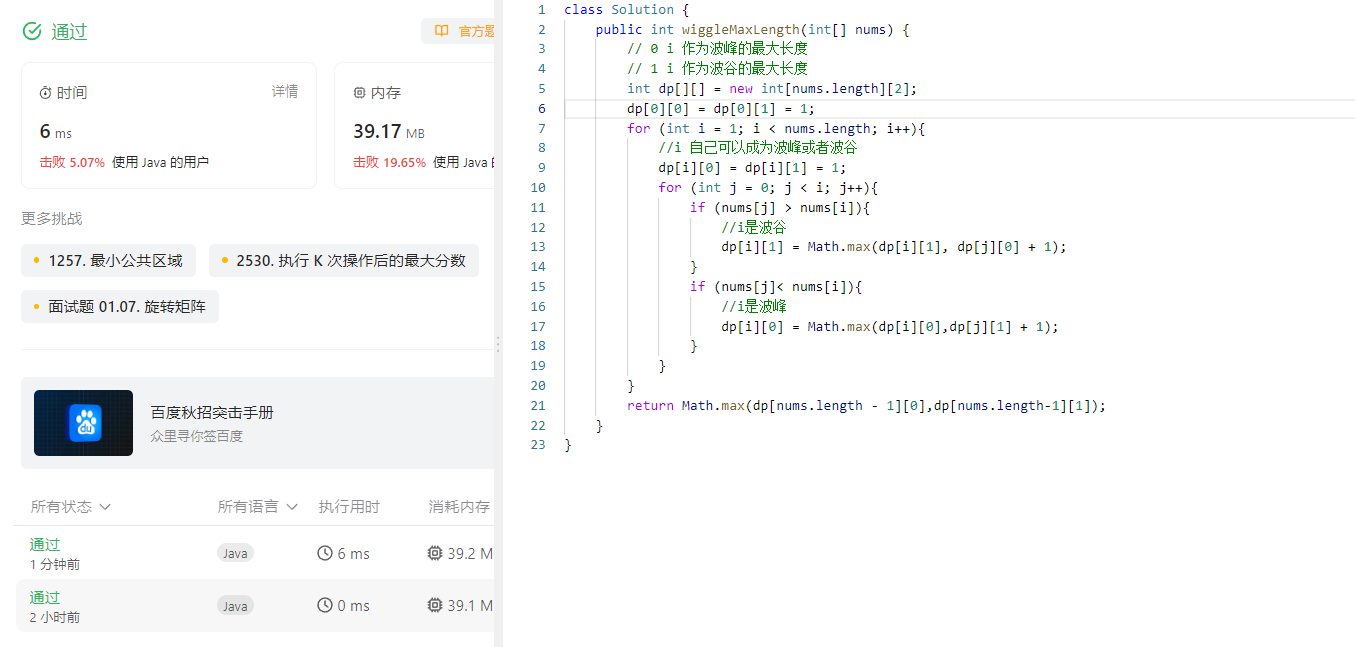
解题思路:
//就是贪心,上升的时候,选取上升数中的较大值
// 下降的时候,选取下降数中的较小值
//然后因为是摆荡数列嘛,就是要开局确认一下是先递增,还是先递减
参考代码:
_376摆动序列
package 代码随想录.贪心算法;
public class _376摆动序列 {
/**
*
* @param nums
* @return
*/
public int wiggleMaxLength(int[] nums) {
//就是贪心,上升的时候,选取上升数中的较大值
// 下降的时候,选取下降数中的较小值
//然后因为是摆荡数列嘛,就是要开局确认一下是先递增,还是先递减
if (nums.length <= 1){
return nums.length;
}
// //看增减顺序
// boolean flag = true; //true增 ,false减
//当前差值
int curDiff = 0;
//上一个差值
int prevDiff = 0;
// int preA = nums[0];
// int preB = nums[1];
// if (preB - preA < 0){
// //先减
// flag = false;
// }
// int maxValue = preB;
// for (int i=2;i< nums.length;i++){
// if (flag = )
//
// }
int count = 1;
for (int i = 1; i < nums.length; i++){
//得到当前差值
curDiff = nums[i] - nums[i-1];
//如果当前差值和上一个差值为一正一负
//等于0的情况表示初始时的preDiff
if ((curDiff > 0 && prevDiff <= 0) || (curDiff < 0 && prevDiff >= 0)){
count++;
prevDiff = curDiff;
}
}
return count;
}
}
_376摆动序列
package 代码随想录.动态规划;
import java.util.Map;
public class _376摆动序列 {
/**
*
* @param nums
* @return
*/
public int wiggleMaxLength(int[] nums) {
// 0 i 作为波峰的最大长度
// 1 i 作为波谷的最大长度
int dp[][] = new int[nums.length][2];
dp[0][0] = dp[0][1] = 1;
for (int i = 0; i < nums.length; i++){
//i 自己可以成为波峰或者波谷
dp[i][0] = dp[i][1] = 1;
for (int j = 0; j < i; j++){
if (nums[j] > nums[i]){
//i是波谷
dp[i][1] = Math.max(dp[i][1], dp[i][0] + 1);
}
if (nums[j]< nums[i]){
//i是波峰
dp[i][0] = Math.max(dp[i][0],dp[j][1] + 1);
}
}
}
return Math.max(dp[nums.length - 1][0],dp[nums.length-1][1]);
}
}
错误经验吸取
文章来源:https://blog.csdn.net/weixin_43554580/article/details/134995261
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!