寻找目标元素

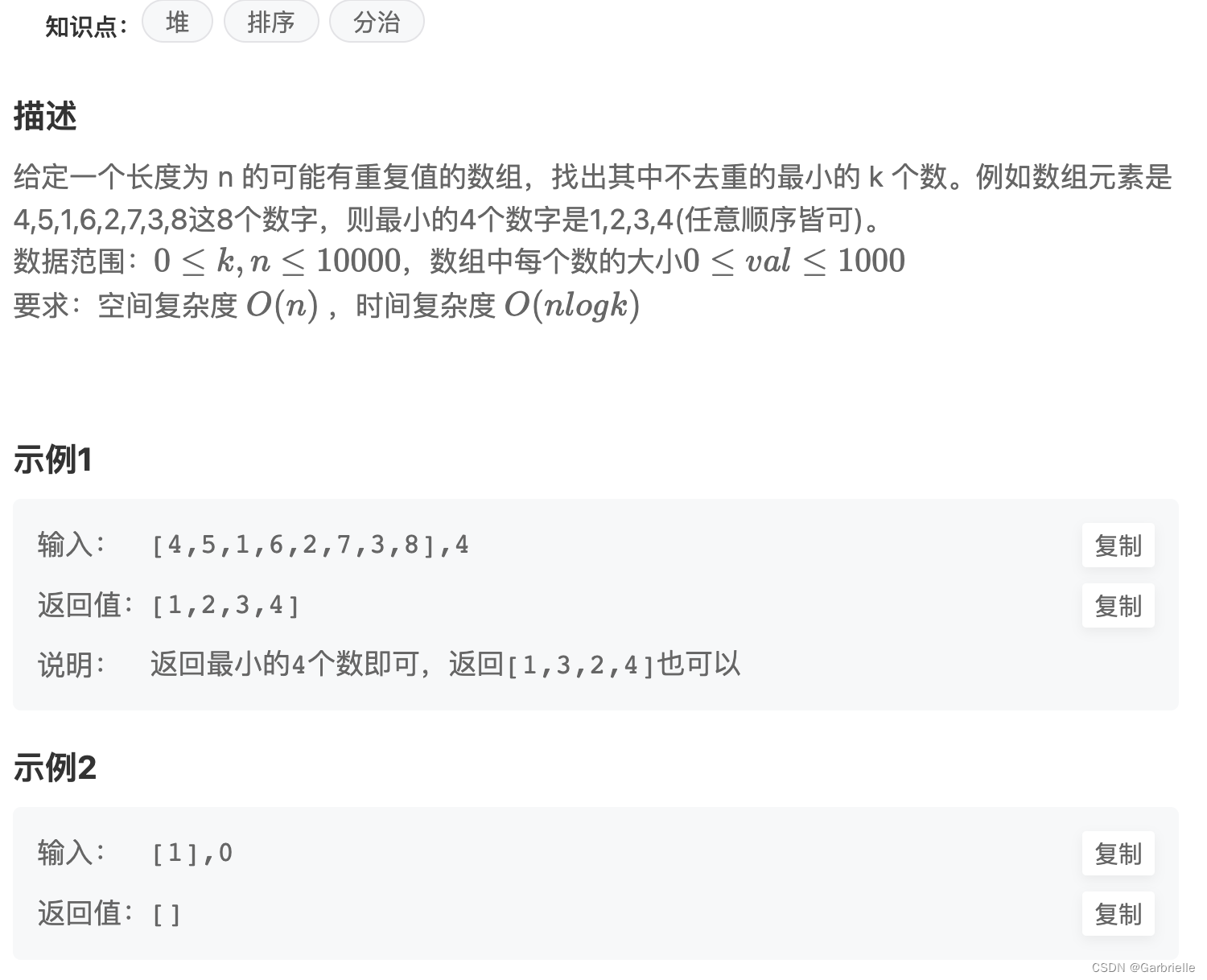
最小的K个数

要求：时间复杂度：O(nlogk),空间复杂度：O(1)

方法1: 冒泡排序

时间复杂度：O(nk),空间复杂度：O(1)

原理： 利用冒泡排序一趟排序可以使一个元素归位的性质，排序K趟，即可得到最小的K个数。

function GetLeastNumbers_Solution(input, k) {
    const res = [];
    if (k > input.length) return input;
    for (let i = 0; i < k; i++) {
        for (let j = 0; j < input.length; j++) {
            if (input[j] < input[j + 1]) {
                [input[j], input[j + 1]] = [input[j + 1], input[j]];
            }
        }
        res.push(input[input.length - i - 1]);
    }
    return res;
}

方法2: 堆排

时间复杂度：O(nlogk), 插入容量为k的大根堆时间复杂度为O(logk), 一共遍历n个元素
空间复杂度：O(k)

原理：建立一个容量为k的大根堆的优先队列。遍历一遍元素，如果队列大小 < k, 就直接入队，否则，让当前元素与队顶元素相比，如果队顶元素大，则出队，将当前元素入队。

function GetLeastNumbers_Solution(input, k) {
    const queue = [],
        res = [];
    if (k === 0 || k > input.length) return res;
    for (let i = 0; i < input.length; i++) {
        if (queue.length < k) {
            // 构建大顶堆
            queue.push(input[i]);
            buildMaxHeap(queue);
        } else {
            if (input[i] < queue[0]) {
                queue.shift();
                queue.push(input[i]);
                buildMaxHeap(queue);
            }
        }
    }
    while (queue.length) {
        res.push(queue[0]);
        queue.shift();
    }
    // 用例需要
    res.sort();
    return res;
}
function buildMaxHeap(arr) {
    // 从最底部开始
    for (let i = Math.floor(arr.length / 2); i >= 0; i--) {
        heapify(arr, i, arr.length);
    }
}

// 调整的节点的下标i, arr无序的长度len
function heapify(arr, i, len) {
    let left = 2 * i + 1;
    let right = 2 * (i + 1);
    let largest = i;
    if (left < len && arr[left] > arr[largest]) {
        largest = left;
    }
    if (right < len && arr[right] > arr[largest]) {
        largest = right;
    }
    if (largest !== i) {
        change(arr, i, largest);
        heapify(arr, largest, len);
    }
}

function change(arr, i, j) {
    let temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

方法3: 快排思想

时间复杂度：平均时间复杂度为O(n), 每次partition的大小为n + n / 2 + n / 4 +… = 2n, 最坏时间复杂度为O(n ^ 2), 因为每次partition都只减少一个元素
空间复杂度：O(1)

原理： 对数组[l, r]一次快排partition过程可得到，[l, p), p, [p + 1, r) 三个区间, [l, p) 为小于等于p的值
[p + 1, r) 为大于等于p的值。
然后再判断p，利用二分法
1. 如果[l, p), p，也就是p + 1个元素（因为下标从0开始），如果p + 1 == k, 找到答案
2. 如果p + 1 < k, 说明答案在[p + 1, r) 区间内，
3. 如果p + 1 > k, 说明答案在[l, p) 内

function GetLeastNumbers_Solution(input, k) {
    const res = [];
    if (k === 0 || k > input.length) return res;
    let l = 0, r = input.length;
    while (l < r) {
        let p = partition(input, l, r);
        if (p + 1 === k) {
            return input.slice(0, k);
        }
        if (p + 1 < k) {
            l = p + 1;
        } else {
            r = p;
        }
    }
    return res;
}
function partition(input, l, r) {
    let pivot = input[r - 1];
    let i = l;
    for (let j = l; j < r - 1; ++j) {
        if (input[j] < pivot) {
            [input[i], input[j]] = [input[j], input[i]];
            i++;
        }
    }
    [input[i], input[r - 1]] = [input[r - 1], input[i]];
    return i;
}

寻找第K大

利用最小的K个数的方法三和方法二的原理，利用堆和快排算法去处理。

function findKth(a, n, K) {
    let l = 0,
        r = n;
    let targetIndex = n - K;
    while (l < r) {
        let p = partition(a, l, r);
        if (p === targetIndex) {
            return a[targetIndex];
        }
        if (p < targetIndex) {
            l = p + 1;
        } else {
            r = p;
        }
    }
}