有趣的数学 数学建模入门三 数学建模入门示例两例 利用微积分求解
一、入门示例1
1、问题描述
???????某宾馆有150间客房,经过一段时间的经营,该宾馆经理得到一些数据:如果每间客房定价为200元,入住率为55%;定价为180元,入住率为65%;定价为160元,入住率为75%;定价为140元,入住率为85%。
????????经理想要使每天的收入最高,问每间客房的定价应为多少?
2、模型假设
????????假设1:每间客房的最高定价为200元。
????????假设2:根据题目提供的数据,可设随着房价的下降,入住率呈线性增长。
????????假设3:宾馆的每间客房的定价相等。
3、模型建立
????????设表示宾馆一天的总收入,与200元相比每间客房降低的房价为
元。由假设2可得,每降低1元房价,入住率就增加
。
????????因此,150间客房,最高房价200,1元入住率为0.005,可以如下公式:
????????由,可知
。于是问题转化为求当
时,总收入
的最大值是多少?
4、模型求解
? ? ? ? 我们整理一下上面的方程。
? ? ? ?
????????
? ? ? ? 然后利用一元函数微分,令
? ? ? ? 可得当,即房价定为155元时,可获得最高收入18018.75元。此时,相应的入住率为77.5%。
二、入门示例2
1、问题描述
????????人口统计学家已经发现:每个城市的市中心人口密度最大,离市中心越远人口越稀少、密度越小。最为常见的人口密度模型为(每平方千米人口数),其中
,
为大于0的常数,
是距市中心的距离。如何求某城市的总人口数?
????????根据相关数据:某城市市中心的人口密度为:。
????????在距离市中心10km时的人口密度为:。
????????该城市为半径30km的圆形区域。
2、问题分析
????????为了确定区间,设市中心位于坐标原点,于是,从而人口密度函数为
。
3、模型求解
????????先确定人口密度中的常数a,c。
????????由,
;
,
,可得
,
,
????????因此人口密度函数为:
????????从而该城市的总人口数就是人口密度函数的积分,其中积分区域D为,
,即
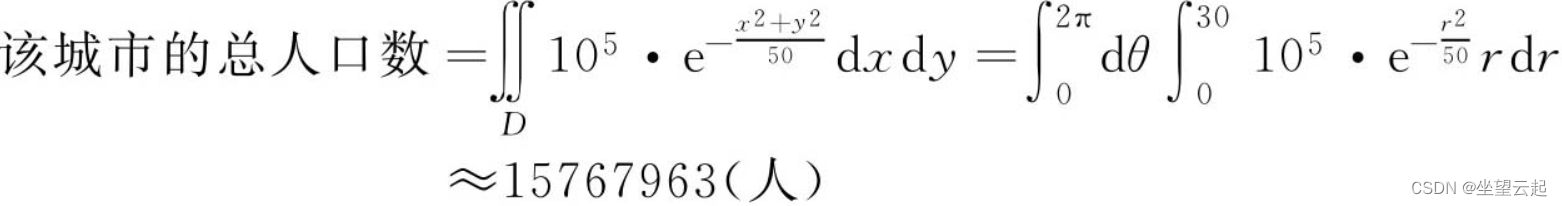
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!