《矩阵分析》笔记
来源:【《矩阵分析》期末速成 主讲人:苑长(5小时冲上90+)】https://www.bilibili.com/video/BV1A24y1p76q?vd_source=c4e1c57e5b6ca4824f87e74170ffa64d
这学期考矩阵论,使用教材是《矩阵论简明教程》,因为没时间听太长的课,就看了b站上这个视频,笔记几乎就是原视频copy,和教材相比有一些没提到(如奇异值分解、Householder矩阵、Given矩阵、广义逆矩阵等),但大部分有,可供参考。
目录
第1章 线性空间和线性变换
考点一:线性空间的基与维数
-
线性空间:若同时满足封闭性和8条规则,则称非空集合V为数域P上的线性空间
-
基底:V中线性无关的一组向量,其他元组都可以被他们线性表示, d i m V = n dimV=n dimV=n
-
子空间:W对于线性空间V所定义的加法运算和数乘运算也构成P上的线性空间,则称W为V的线性子空间,简称子空间
-
生成子空间
? 设α1,α2,…,αm是V上的m个元素,由这m个元素的任意组合构成的集合{k1α1+k2a2+…kmam}对V中的加法及数乘封闭,因而这个子集是V中的子空间,记作:L(α1,α2,…,αm)
? (1)V1∩V2 (2)V1+V2
-
求和子空间的方法
-
维数定理: d i m V ? 1 ? + d i m V ? 2 ? = d i m ( V ? 1 ? + V ? 2 ? ) + d i m ( V ? 1 ? ∩ V ? 2 ? ) dimV~1~+dimV~2~ = dim(V~1~+V~2~) + dim(V~1~∩V~2~) dimV?1?+dimV?2?=dim(V?1?+V?2?)+dim(V?1?∩V?2?)
【例1.1】求V1+V2的维数及一个基
? 向量竖写为矩阵,化为阶梯形,一组极大无关组就是一个基,维数为阶梯数
考点二:证明线性变换
-
变换:设V是P上的线性空间,从V到V的映射称为V中的变换(线性变换是常见的变换)
-
线性变换:设T是V上的变换,如果对于任意的α,β∈V,k∈P都有
? T ( a + b ) = T a + T b ; T ( k a ) = k T a T(a+b)=Ta+Tb; T(ka) = kTa T(a+b)=Ta+Tb;T(ka)=kTa ,则称T为V上的线性变换
【例1.2】定义变换T如下:TA= CA-AC。证明: T是线性变换
? 把A替换为a+b、ka,列出T(a+b),Ta+Tb,T(ka),kTa
考点三:像子空间、核子空间(用线性变换定义的子空间)
-
像子空间: T V = T α ∣ α 属于 V TV={Tα|α属于V} TV=Tα∣α属于V
像子空间是由V中所有元素的像Tα构成的(Tα是α通过线性变换T得到的,α∈V)
-
核子空间: T ? 1 ( 0 ) = k e r T = α ∣ α ∈ V , T α = 0 T^{-1}(0) = kerT = {α|α∈V,Tα=0} T?1(0)=kerT=α∣α∈V,Tα=0
核子空间中的元素α在线性变换T的作用下转换为0
-
例如:投影变换{(x1, x2, x3)}三维空间
? T(x1, x2, x3) = (x1, x2, 0)
? TV = {(x1, x2, 0)},二维空间,维数为2
? T’(0) = {(0, 0, x3)},一维空间,维数为1
- 维数定理2:设T是n维空间上的线性变换,则 d i m T V = d i m T ? 1 ( 0 ) = n dimTV = dimT^{-1}(0)=n dimTV=dimT?1(0)=n
考点四:线性变换的矩阵(求线性变换T在某基底下的矩阵)
-
用矩阵A来表达线性变换T
定义: ( T α 1 , T α 2 , . . . , T α n ) = ( α 1 , α 2 , . . . , α n ) A (Tα_1,Tα_2,...,Tα_n) = (α_1,α_2,...,α_n)A (Tα1?,Tα2?,...,Tαn?)=(α1?,α2?,...,αn?)A
-
求同一个线性变换在不同基底下的矩阵

p.s. 求逆方法:(A|E)–>(E|A-1)
【例1.4】

第2章 内积空间
考点一:内积空间的定义
-
定义:

-
元素大小:

考点二:标准正交基
-
标准正交基:

-
用施密特(Schmidt)正交化的方法求标准正交基

【例2.1】


考点三:正规矩阵的对角化
-
定义:

此时V叫作复内积空间或者酉空间 -
酉矩阵的定义:设A∈Cn×n且AHA=AAH=E,则称A为酉矩阵
-
正规矩阵的定义:设A∈Cn×n且AHA=AAH,则称A为正规矩阵
-
对角形矩阵、实对称矩阵、反实对称矩阵、厄密特矩阵、反厄密特矩阵、正交矩阵、酉矩阵都是正规矩阵
-
正规矩阵对角化:正规矩阵一定可以对角化,即存在酉矩阵U使得UHAU= Λ, Λ的对角线元素为A的特征值
第3章 矩阵的标准形
考点一:哈密顿-凯莱(Hamilton-Cayley)定理
-
哈密顿凯莱定理:每个n阶矩阵都是它的特征多项式的根。
设A为n阶矩阵,$f(λ)=|λE-A|=λn+a_{n-1}λ{n-1}+…+a_1λ+a_0 $
? 则 f ( A ) = A n + a n ? 1 A n ? 1 + . . . + a 1 A + a 0 E = 0 f(A)=A^n+a_{n-1}A^{n-1}+...+a_1A+a_0E=0 f(A)=An+an?1?An?1+...+a1?A+a0?E=0
-
简化运算:求φ(A)
? φ ( λ ) = f ( λ ) ? q ( λ ) + r ( λ ) φ(λ)=f(λ)·q(λ)+r(λ) φ(λ)=f(λ)?q(λ)+r(λ)
? φ ( A ) = f ( A ) ? q ( A ) + r ( A ) = 0 + r ( A ) = r ( A ) φ(A)=f(A)·q(A)+r(A)=0+r(A)=r(A) φ(A)=f(A)?q(A)+r(A)=0+r(A)=r(A)
【例3.1】


考点二:最小多项式
-
特征多项式: f ( λ ) = ∣ λ E ? A ∣ f(λ)=|λE-A| f(λ)=∣λE?A∣,称为矩阵A的特征多项式
-
零化多项式:若A是一个方针,φ(λ)是一个多项式, φ ( λ ) = a m λ m + a m ? 1 λ m ? 1 + . . . + a 1 λ + a 0 φ(λ)=a_mλ^m+a_{m-1}λ^{m-1}+...+a_1λ+a_0 φ(λ)=am?λm+am?1?λm?1+...+a1?λ+a0?,则称φ(λ)是A的零化多项式
-
特征多项式就是矩阵A的零化多项式;特征多项式×任一多项式还是零化多项式;零化多项式有无穷多个
-
最小多项式:设A∈Cn×n,在A的零化多项式中,次数最低的首项系数为1的多项式,称为矩阵A的最小多项式,记作m(λ)
-
最小多项式的跟<==>特征多项式(对同一矩阵而言)
设矩阵A属于Cn×n的所有特征值λ1,…,λs,A的特征多项式为f(λ)=|λE-A|
则A的最小多项式一定具有如下形式: m ( λ ) = ( λ ? λ 1 ) n 1 ( λ ? λ 2 ) n 2 . . . ( λ ? λ s ) n s m(λ)=(λ-λ_1)^{n_1}(λ-λ_2)^{n_2}...(λ-λ_s)^{n_s} m(λ)=(λ?λ1?)n1?(λ?λ2?)n2?...(λ?λs?)ns?
【例3.2】

考点三:约当标准形(Jordan标准形)
-
λ矩阵:设矩阵A的元素都是λ的多项式,形如

-
行列式因子:A(λ)中所有非零的k阶子式的首项系数为1的最大公因式,D(λ),称为A的一个k级行列式因子
-
不变因子:d1=D1,d2=D2/D1,d3=D3/D2,…,dn=Dn/Dn-1
-
初级因子:把每个次数大于零的不变因子分解为互不相同的一次因式的方幂的乘积,所有这些一次因式的方幂(相同的必须按出现次数计算),称为A的初级因子
-
约当标准形定义:称ri阶矩阵

-
求约当标准形的方法
- 法一:用行列式因子法
【例3.3】

(二阶有9个,略)

考点四:史密斯标准形(Smith标准形)
-
矩阵A的初等变换
-
互换矩阵A的任意两行/列
-
以非零的数k乘A的某一行/列
-
以多项式φ(λ)乘以A的某一行/列,加到另一行/列上
(以上三种变换不会改变行列式因子)
-
-
史密斯标准形:

-
任一个非零多项式矩阵A都可以经过初等变换化为史密斯标准形
-
化为史密斯标准形的具体步骤
-
先确定左上角第一个元素d1=D1(一阶行列式因子)
-
将d1所在的行和列的其他元素都消为0(通过初等变换),得到
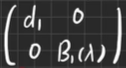
-
再确定新矩阵B1(λ)的左上角第一个元素d2=新D1‘(新D1‘为新矩阵B1(λ)的一阶行列式因子)
得到

-
重复这个过程,即可得到史密斯标准形

-
【例3.4】求Smith标准形和不变因子

考点五:用史密斯标准形方法求解约当标准形(法二)常用
- 史密斯标准形
【例3.5】求约当标准形


第4章 向量和矩阵的范数
考点一:证明向量范数
- 向量范数的定义:

则称||x||为Cn上的向量范数,简称向量范数
- 常用的向量范数

【例4.1】

考点二:证明矩阵范数
1.矩阵范数的定义:

-
常用的矩阵范数


-
相容性:

-
谱半径:

-
谱半径与范数:
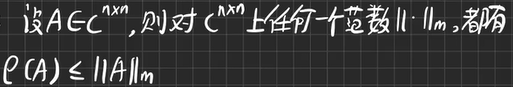
【例4.2】

考点三:范数与正规矩阵的证明题
-
正规矩阵对角化:正规矩阵一定可以对角化,即存在酉矩阵U使得UHAU= Λ, Λ的对角线元素为A的特征值
【例4.3】

第5章 矩阵的分解
考点一:矩阵的三角分解
-
Dolittle分解法(A=LR)
矩阵特点(以三阶为例)
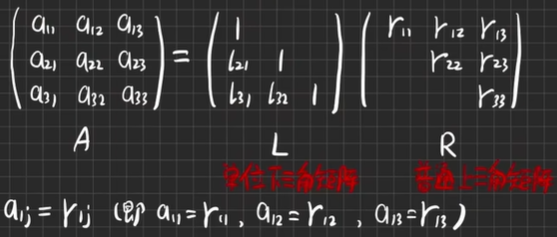
【例5.1】求矩阵的Dolittle分解

考点二:矩阵的QR分解
-
QR分解定理:A=QR(A: n阶复矩阵,Q: 酉矩阵,R: 上三角矩阵)
-
QR分解的一般步骤(以三阶方矩为例)
-
把矩阵A写成列向量的形式:A=(α1,α2,α3)
-
用施密特正交化方法,把α1,α2,α3正交化
-
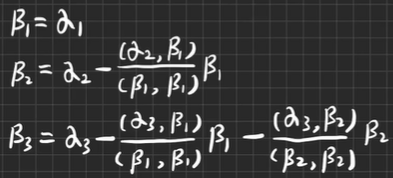


-
【例5.2】 求矩阵的QR分解



考点三:矩阵的满秩分解
-
满秩分解:将矩阵A分解为列满秩×行满秩矩阵,形如:

-
满秩分解的一般步骤
- 作初等行变换:


- 作初等行变换:
【例5.3】求矩阵的满秩分解



第6章 矩阵的函数
考点一:矩阵的导数(对一个变量的导数)
-
函数矩阵:以实变量t的实函数aij(t)为元素的矩阵

-
函数矩阵对一个变量的导数
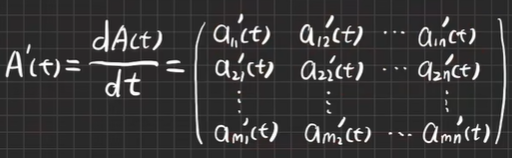
【例6.1】求dA/dt

考点二:矩阵的幂级数
-
矩阵幂级数:设 A = ( a i j ∈ C n × n ) A=(a_{ij}∈C^{n×n}) A=(aij?∈Cn×n),称形如
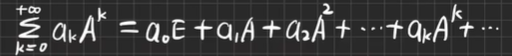
-
收敛性:设幂级数Σk=0akxk的收敛半径为R,A∈Cn×n则
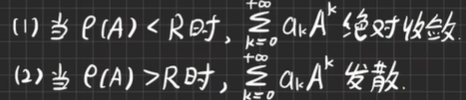
-
收敛半径:R=1/ρ,ρ=limk->∞=|ak+1/ak|
【例6.2】判断矩阵幂级数

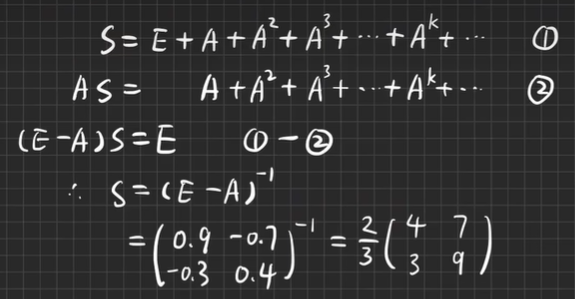
考点三:矩阵函数(A–>f(At)) 常见(A–>eAt)
-
计算矩阵函数的方法:最小多项式法
-
计算矩阵函数的一般步骤:

【例6.3】求矩阵函数eAt




考点四:矩阵函数在微分方程组中的应用
-
一阶线性常系数齐次微分方程组
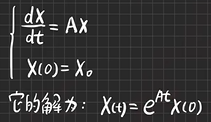
-
一阶线性常系数非齐次微分方程组
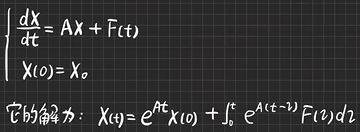
【例6.4】




考点五:矩阵函数的性质(eAt–>A)
- deAt/dt=AeAt=eAtA,则[deAt/dt]|t=0=AdeA·0=Ae0=A
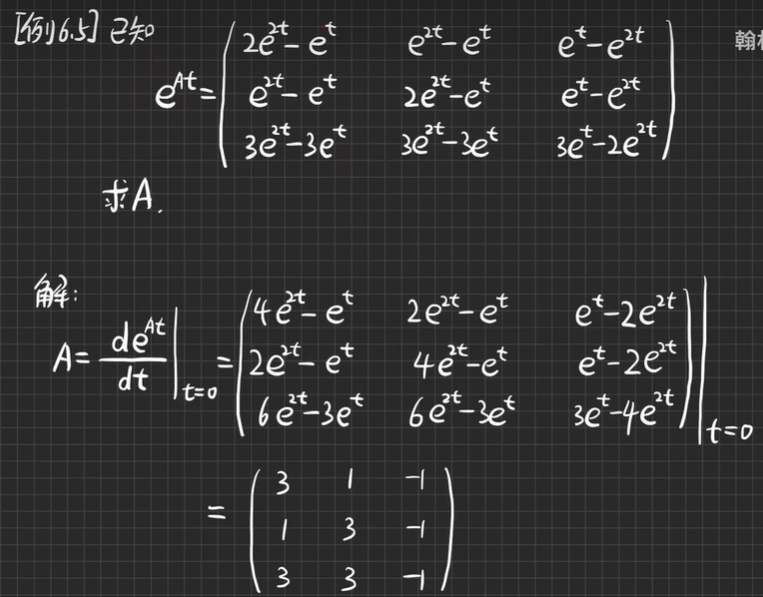
第7章 矩阵特征值的估计
考点一:Gerschgorin盖尔圆定理
-
盖尔圆定义

-
盖尔圆定理:矩阵A∈Cn×n的全体特征值都在它的n个盖尔圆构成的并集之中
-
A的列盖尔圆:A∈Cn×n与AT的特征值相同,根据盖尔圆定理A的特征值也在AT的n个盖尔圆构成的并集之中,称AT的盖尔圆为A的列盖尔圆
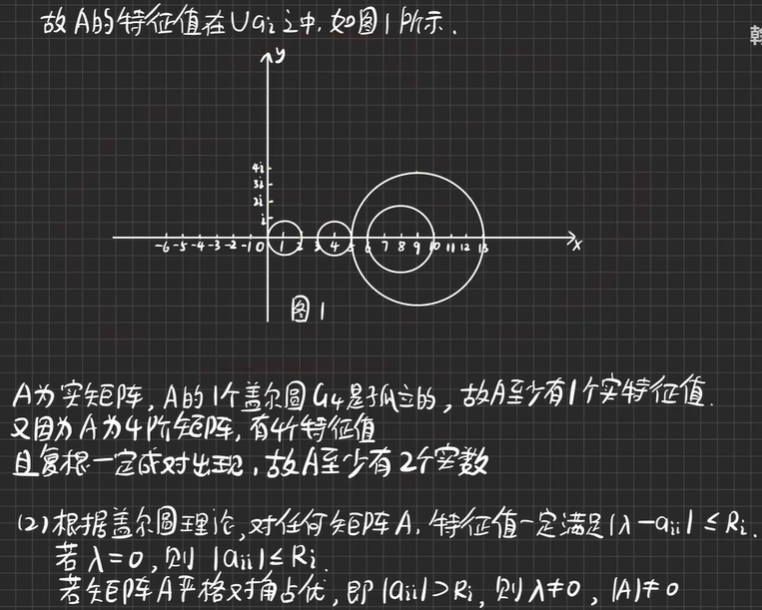
【例7.1】估计矩阵的特征分布


- 推论:若A为实矩阵A∈Rn×n,且A的n个盖尔圆是孤立的,则A有n个互不相同的实特征值
【例7.2】画出矩阵盖尔圆草图、矩阵能够对角化吗?


-
根据盖尔圆理论,对任何矩阵A,特征值一定满足|λaii|≤Ri,
若λ=0,则|λaii|≤Ri,
若矩阵A严格对角占优,即|λaii|>Ri,则λ≠0,|A|≠0
-
A为实矩阵,特征方程|λE-A|=0为实代数方程,它的复根一定成对出现,一定是共轭的,即a±ib的形式
【例7.3】

第8章 矩阵的直积(Kronecker积)
考点一:直积
- 直积的定义:设矩阵A=(aij)m×n,B=(bij)p×q,

【例8.1】

- 矩阵直积的性质


【例8.2】求A?B的一个特征值和特征向量

【例8.3】

【例8.4】

考点二:拉直
-
拉直的定义:
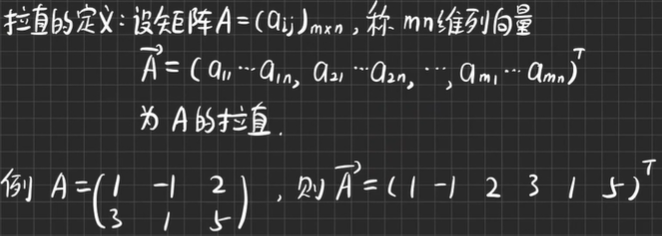
-
拉直的性质:
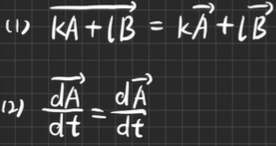

(改错) A B ( 拉直 ) = ( A ? E ? p ? ) B ( 拉直 ) AB(拉直)=(A?E~p~)B(拉直) AB(拉直)=(A?E?p?)B(拉直)(按B展开)- 定理

? A ? E ? n ? ( 改为 ) ? > A ? E ? p A?E~n-(改为)->A?E~p A?E?n?(改为)?>A?E?p
- 定理
【例8.5】

? ∵ ( A ? B ) ( x ? y ) = ( A x ) ? ( B y ) ∴ ( A ? E n ) ( E m ? B T ) = ( A ? B T ) ∵(A?B)(x?y)=(Ax)?(By) ∴(A?En)(Em?BT)=(A?BT) ∵(A?B)(x?y)=(Ax)?(By)∴(A?En)(Em?BT)=(A?BT)
- 线性矩阵方程组:设A∈Cm×m,B∈Cn×n,F∈Cm×n,X∈Cm×n

【例8.6】

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!