【数据结构—堆排序、top k问题和时间复杂度】

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

---

前言

提示：这里可以添加本文要记录的大概内容：

世上有两种耀眼的光芒，一种是正在升起的太阳，一种是正在努力学习编程的你!一个爱学编程的人。各位看官，我衷心的希望这篇博客能对你们有所帮助，同时也希望各位看官能对我的文章给与点评，希望我们能够携手共同促进进步，在编程的道路上越走越远！

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、堆排序（升序）

实现数组的排序：

方法一：利用堆来实现排序的话，但是realloc()函数来申请空间。

方法二：我们可以把一个现有数组直接建堆，可以不用申请额外的空间，直接在数组这个结构上直接动手。

1.1向上调整算法：

1.2向下调整算法：

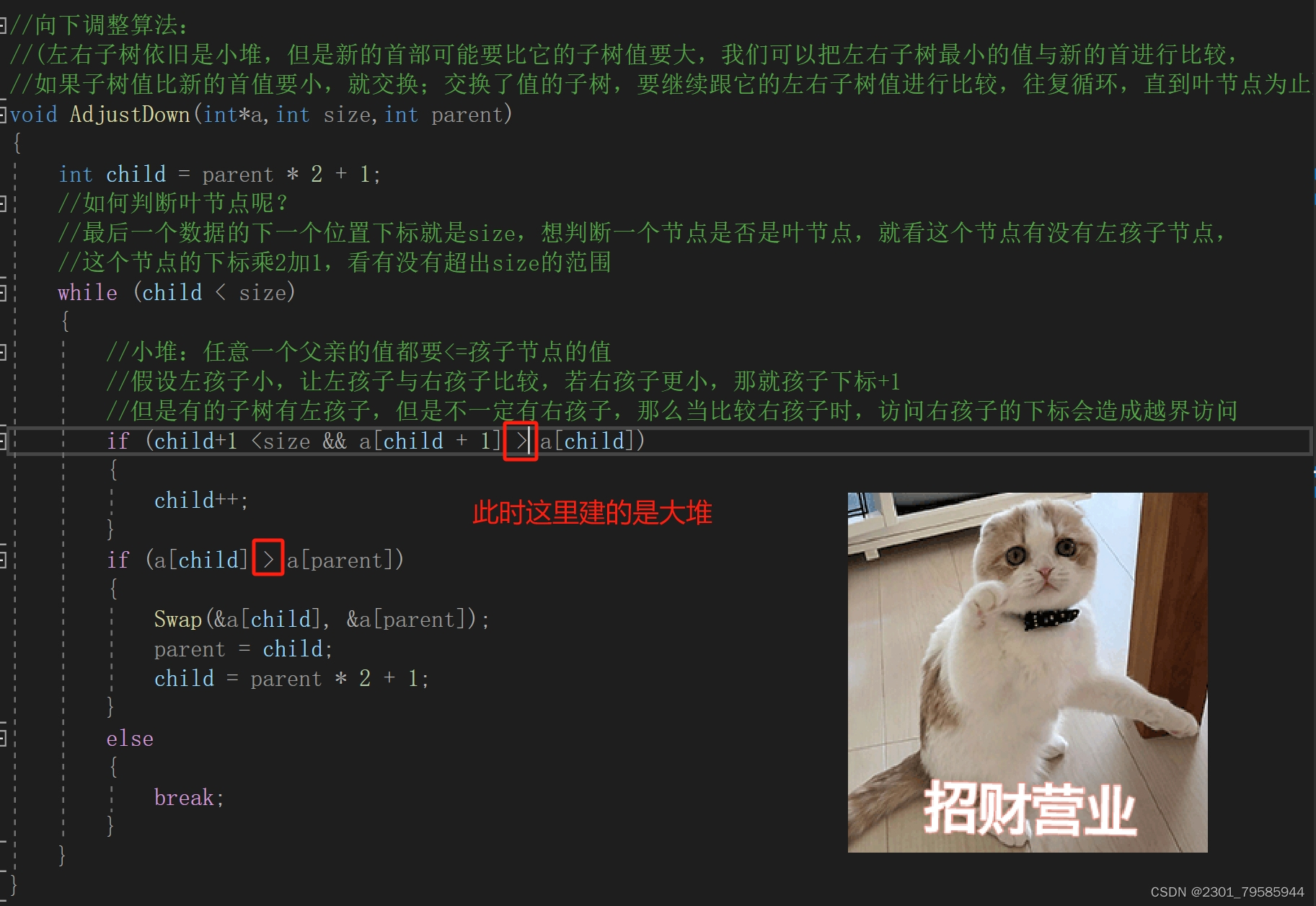
1.3、堆排序的实现：

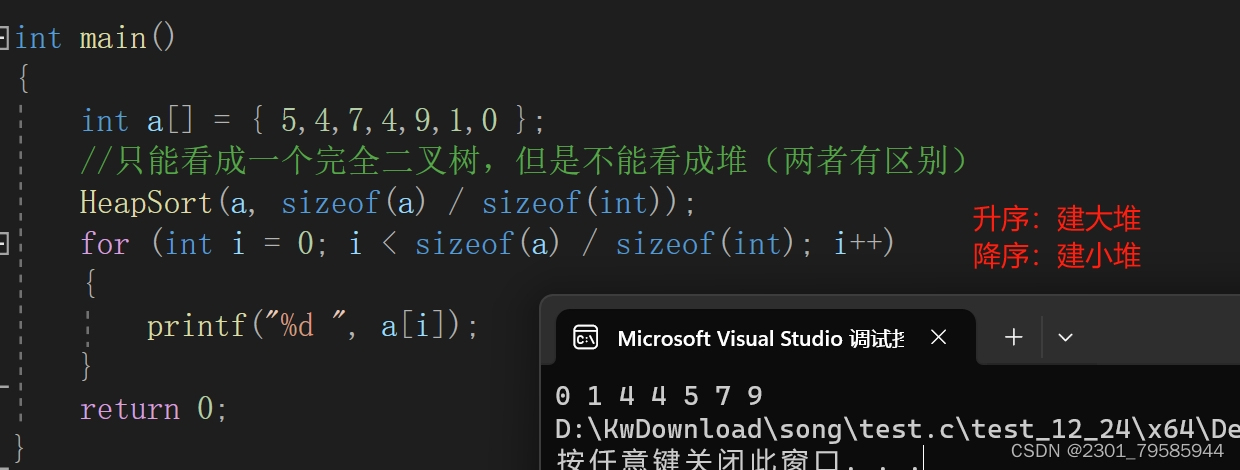
升序：要建大堆【先选出最大的数，然后把首位的值一交换，相当于最后一个数排好了，那最后一个数就不要动了，可以把最后一个数不在看作堆内的数据，此时堆的左、右子树还是堆的形式，我们便把堆的首位数向下调整，我们便可以得到第二位最大的数，我们再次首位的值交换，然后把第二位最大的数也排除堆的范围之内；循环往复。
时间复杂度：（一次建堆：1*LogN;选数：(N-1)*LogN）】
(为什么不用小堆呢？小堆的话，只能选出最小的数，但如何选出次小的数呢？
如果我们取出最小的数，剩下的数可能是堆，也可能不是堆；若把剩下的数看成堆，那么关系全乱了(兄弟和叔侄之间没有大小关系)，所以我们只能把剩下的数重新建堆，代价是：每建一次堆的时间复杂度为：O(LogN)，这个方法不好)

时间复杂度：算的是量级，有时候时间复杂度是一样的，但是他们的效率是不一样的，在性能上是有差异的。

二、top k问题

top k问题：N个数里面找最大的前k个（N远大于k)
思路1：

N个数插入到大堆里面，Pop K次。
时间复杂度：一个数插入最多是高度次：LogN;N个数插入是：N*LogN次；取K个数是：K*LogN次，最终是O(N*LogN)。
思路2：

1、读取前K个值，建立k个数的小堆；
2、依次在读取后面的值，跟堆顶比较，如果比堆顶大，就替换堆顶的值，进堆，再向下调整。

2.1top k问题的代码实现：

//创造通过的随机数
void GreateNDate()
{
	//造数据
	int n = 10000000;
	srand(time(0));
	const char* file = "data.txt";
	//以写的形式将文件打开
	FILE* fin = fopen(file, "w");
	//fin:写  fout:读
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (int i = 0; i < n; i++)
	{
		//我们产生一千万个数，直接用rand()是不行的
		//因为库里面的随机数最多只能产生三万多个，所以会有997万个数是重复的；
		//我们给rand()+i会大大减小重复
		int x = (rand() + i) % 10000000;
		fprintf(fin, "%d\n", x);//写入文件中
	}
	fclose(fin);
}

//找出top k中最大的前k个数据
void PrintTopK(const char* file, int k)
{
	//以读的形式将文件打开
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}
	//建一个k个数的小堆
	int* minheap = (int*)malloc(sizeof(int) * k);
	if (minheap == NULL)
	{
		perror("malloc error");
		return;
	}
	//读取前k个，建小堆
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minheap[i]);
		AdjustUp(minheap, i);
	}

	int x = 0;
	//把文件中的数据读取出来到x中
	while (fscanf(fout, "%d", &x) != EOF)
	{
		//剩下的数与小堆的堆顶进行比较，并把大的数替换
		if (x > minheap[0])
		{
			minheap[0] = x;
			AdjustDown(minheap, k, 0);
		}
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", minheap[i]);
	}
	printf("\n");
	fclose(fout);
}

int main()
{
	//GreateNDate();
	PrintTopK("data.txt", 3);
	return 0;
}

?2.2如何保证取出的前k个数就是N个数里面最小的前k个数呢？

我们把随机数都取模1000万，那么随机数都是1000万以内的值；我们挑10个随机位置，该它们的值，让他们的值都大于1000万；那也就意味着随便改这10个位置，都能够把它们的值取出来，就说明取出的是前k个值是最大的，如果取不出来，那就是有问题的。

2.3实际数据测试展示：

三、时间复杂度

时间复杂度：算的是量级，有时候时间复杂度是一样的，但是他们的效率是不一样的，在性能上是有差异的。

---

总结

好了，本篇博客到这里就结束了，如果有更好的观点，请及时留言，我会认真观看并学习。
不积硅步，无以至千里；不积小流，无以成江海。