【面试高频算法解析】算法练习3 双指针

前言

本专栏旨在通过分类学习算法，使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目，帮助您深度理解每种算法，避免出现刷了很多算法题，还是一知半解的状态

---

专栏导航

1. 二分查找
2. 回溯（Backtracking）
3. 双指针
4. 滑动窗口
5. 深度优先搜索
6. 广度优先搜索
7. 贪心算法
8. 单调队列
9. 堆（Heap）

---

算法解析

双指针技术是一种常用的算法策略，它使用两个指针以不同的速度或方向遍历数据结构（通常是线性结构如数组或链表），从而达到解决问题的目的。双指针技术可以帮助我们简化复杂度，减少不必要的运算，尤其是在解决一些与序列相关的问题时非常有效。

双指针通常有以下几种分类：

1. 快慢指针：
   快慢指针通常用于解决链表中的问题，例如检测链表中的循环。快指针每次移动两步，慢指针每次移动一步。如果链表中有循环，则快指针最终会追上慢指针。

2. 左右指针：
   左右指针通常用于有序数组或字符串，开始时一个指向头部（左指针），另一个指向尾部（右指针），然后向中间移动。例如在二分查找、合并两个有序数组或是计算一组数的对数（如两数之和）时会用到。

3. 滑动窗口(面试中很常见我将另开一篇详细介绍)：
   滑动窗口可以看作是一种特殊的双指针，通常用于解决数组/字符串的子区间问题。两个指针共同定义了一个窗口，可以增加或减少窗口的大小以满足特定条件，例如找出满足条件的最长/最短的子数组/子字符串。

双指针技术的优势在于它可以减少时间复杂度。例如，在排序数组中寻找两数之和等于特定值的问题中，暴力解法需要 O(n^2) 的时间复杂度，而使用双指针技术则可以降低到 O(n)。

下面是一个使用双指针（左右指针）解决“两数之和”问题的示例：

def two_sum_sorted(numbers, target):
    left, right = 0, len(numbers) - 1
    while left < right:
        current_sum = numbers[left] + numbers[right]
        if current_sum == target:
            return [left + 1, right + 1]  # 返回的是位置，不是索引
        elif current_sum < target:
            left += 1  # 和太小，移动左指针
        else:
            right -= 1  # 和太大，移动右指针
    return [-1, -1]  # 如果没有找到，返回[-1, -1]

在这个函数中，左指针从数组的开始位置向右移动，右指针从数组的结束位置向左移动，直到找到两数之和等于目标值或左右指针相遇。通过这种方式，我们只需要遍历数组一次，从而提高了算法的效率。

---

实战练习

寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：
输入：nums = [1,3,4,2,2]
输出：2

示例 2：
输入：nums = [3,1,3,4,2]
输出：3

提示：
1 <= n <= 105
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

进阶：
如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

官方题解

---

三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意： 答案中不可以包含重复的三元组。

示例 1：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：
输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：
输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

官方题解

---

删除排序链表中的重复元素II

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

示例 1：

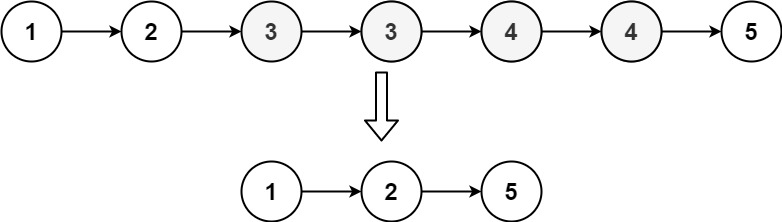
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

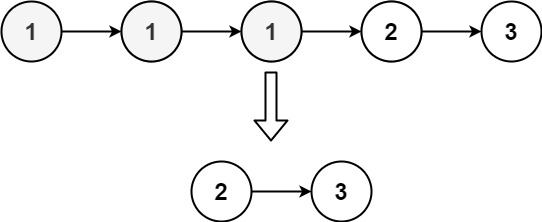
输入：head = [1,1,1,2,3]
输出：[2,3]

提示：
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列

官方题解