组间/组内(I-MR-R/S)控制图
常规控制图
1924年沃特·阿曼德·休哈特提出了控制图方法,这是一种基于统计显著性原则进行过程控制的图形工具。控制图理论用来区分两种变异。
第一种是由“偶然原因”(也称“常见原因”“自然原因”随机原因”"固有原因”或“不可控原因”)引起的随机变异。这是由于有很多种始终存在且不易区分的原因会带来变异;而相对于整个变异,它们中的每一个都只是很小的一部分,并没有产生显著的影响。然而,所有这些无法确定的随机原因的贡献总和是可测量的,并假定是过程固有的。消除或纠正常见原因,可能需要资源分配决策﹐从根本上改变过程和系统。第二种变异代表该过程的真正变化。这种变化可归因于一些可识别的原因,这些原因不是生产过程所固有的,且至少在理论上是可以被消除的。这些可识别的原因被称为变异的“可查明原因”(也称特殊原因、非自然原因、系统性原因或可控原因)。它们可归因于材料缺乏一致性,破损的工具,工艺或程序不完善,设备的性能异常或者环境变化。
如果过程变异只源于随机原因,则称该过程处于统计控制状态,或简称“受控”。该变异水平一旦确定,与该水平的任何偏差都可视为要识别和消除的可查明原因导致的结果。以上内容可以参考GB/T 17989.2-2020

常规控制图使用前提
任何工具使用都有前提,要想使用常规控制图,也需要满足一定的前提,除了大家熟悉的正态、数据独立、MSA合格这些前提外,其实还有一个前提,那就是只能有单一的变异来源。什么叫常规控制图“只能有单一的变异来源”,如果不满足这个前提直接写常规控制图会出现什么后果呢?我们一起来看一个案例。
案例:为芯片镀膜的车间,在连续25天内,每天抽取5片芯片测量其镀膜厚度,测量结果见下表镀膜厚度数据,绘制控制图以判断生产是否正常。
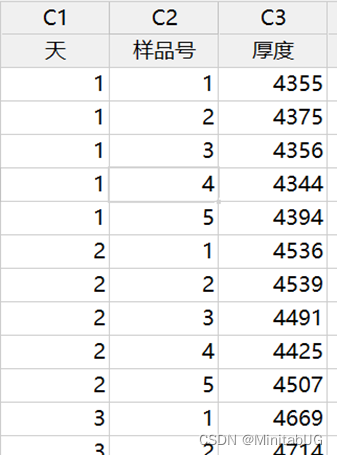
带子组的控制图有两种绘制方法
方法一:种是先求出每组(本例是天)的均值,然后对均值绘制I-MR(单值-移动极差)控制图。
方法二:另一种是直接使用原始数据,绘制Xbar-R(均值-极差)控制图。
方法一:绘制I-MR图的方法是先求出子组均值,将其存入某列(本例是放在C5中),然后再绘制控制图。
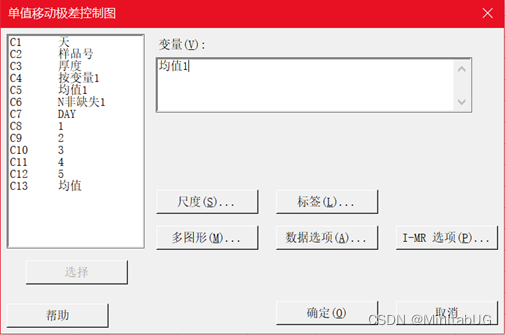
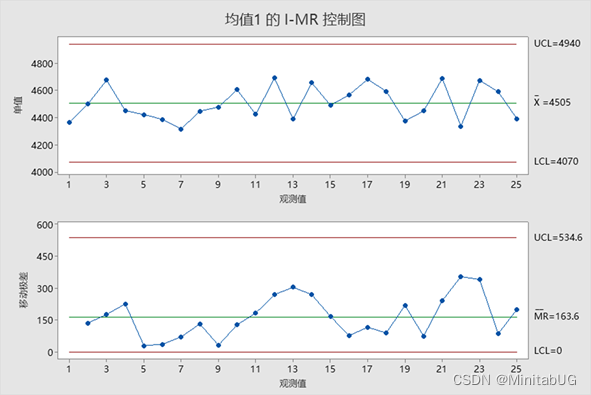
方法二:直接用原始数据绘制Xbar-R(均值-极差)控制图。
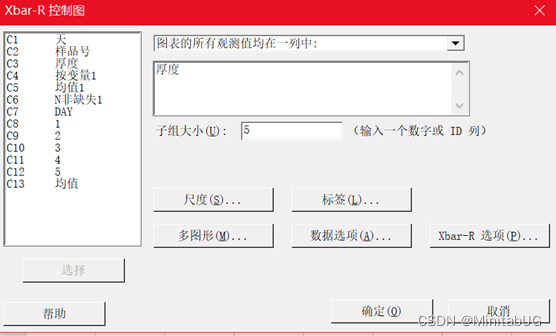
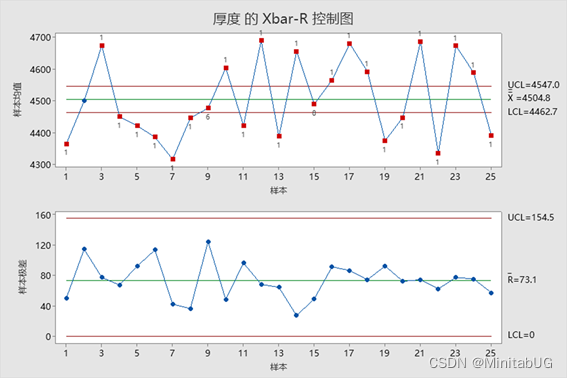
首先我们可以看到,两种方法画控制图结论刚好相反,那么哪一种方法结果是对的呢?要想回答这个问题我们需要了解为什么结果会有差异?如果生产过程数据只有唯一的变异来源,所有数据的波动都来自随机误差的话,二者的估计应该大体相同。如果生产过程数据不只有唯一的变异来源,数据的波动一方面来自随机误差(根据合理子组的原理,组内差反映的就是随机误差),另一方面还来自组间可能有的波动,这样一来,用组间移动极差估计出来的标准差会比仅用组内差(不考虑组间差)估计出来的标准差大很多,这必将导致I-MR控制限会比Xbar-R控制限宽很多,因此才会使I-MR图判断认为过程均值正常,而Xbar-R图判断认为过程均值几乎点点都不正常。那如何判断收集到的数据中波动是否全部来自随机波动?
控制图变异源分析
我们可以用定性+定量的方法帮助评估变异来源。
定性方法-多变异图
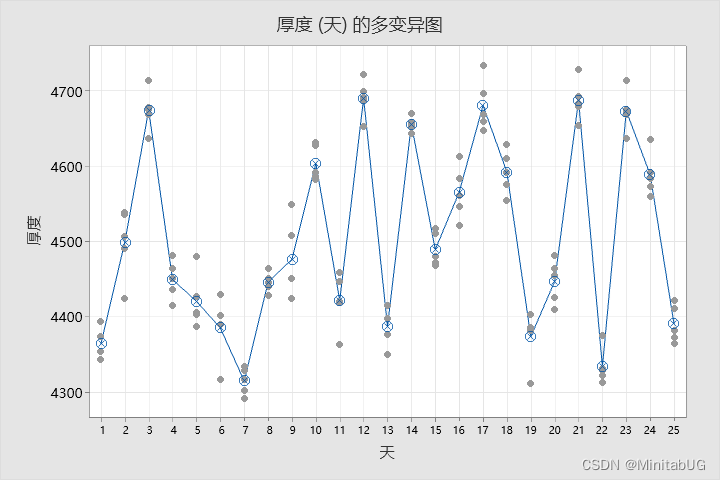
从多变异图可以看出,各天内5个产品(组内变异)厚度的波动都不大,但天与天间(组间变异)的均值相差较大。
定量方法-一般线性模型
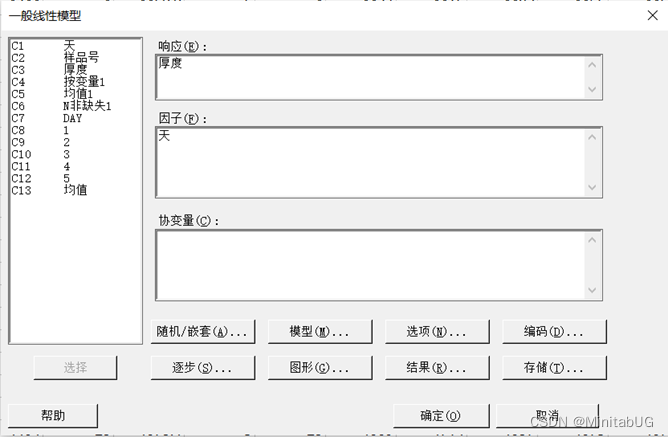
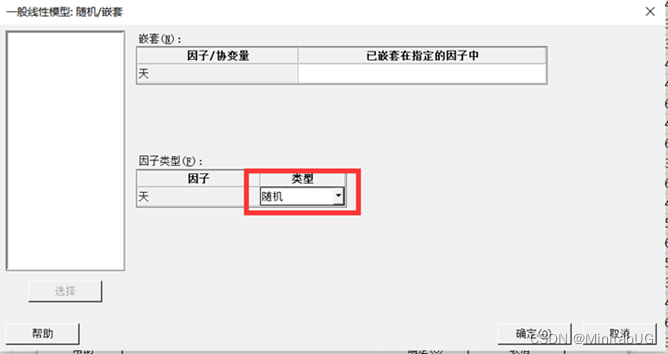
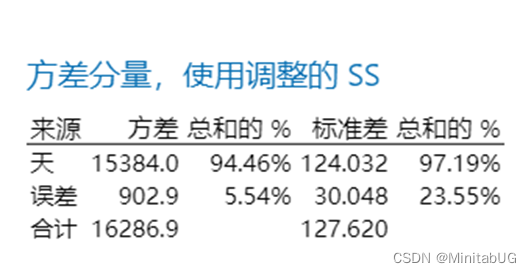
从计算结果可以看出,在数据中,组内差(误差)方差分量为902.900,只占总变异的5.54%。组间差(天)方差分量为15384.000,占总变异的94.46%。通常认为,随机误差的方差分量超过90%时,可以认为随机误差为唯一变异源。也就是说对于当前过程数据变异来源不唯一,不光有组内变异还有组间变异,那如果不能认为随机误差为唯一变异源,该如何进行过程统计控制?
组间/组内控制图
使用组间/组内( I-MR-R/S )控制图可以在每个子组属于不同部件或批次的情况下监视过程的均值以及子组间和子组内的变异。使用此控制图可以监视过程在一段时间内的稳定性,以便您可以标识和更正过程中的不稳定性。
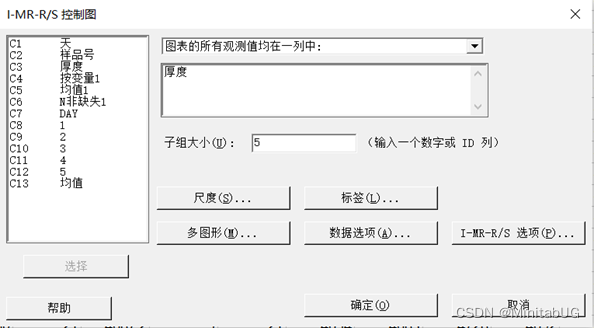
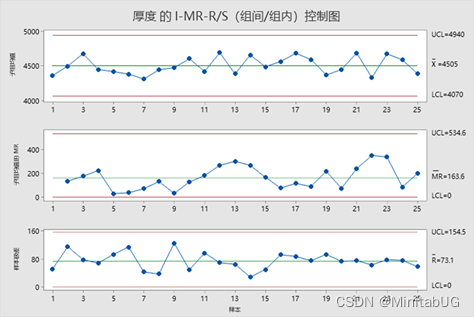
从上图可以看出,I-MR-R/S控制图是由三张图组成的(以前最多只有两张图),其中,上图和中图其实就是方法一的两张图,下图其实就是方法二中下面那张组内极差控制图。读图时,先看组内极差控制图,如果没有异常,说明各组内的波动状况是正常的如果有异常,先要找到该组异常的原因。I-MR-R/S控制图中的组内极差控制图完全正常。在分析极差控制图后,再来看组间的单值-移动极差控制图,看图中是否有异常的组。I-MR-R/S控制图中的单值-移动极差控制图也是正常的。这说明,芯片镀膜生产过程厚度虽然有较严重的组间波动但总体上看还是稳定的。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!