基于神经网络关于冷却装置功率与系统总耗电量的关系模型研究（内附BP神经网络代码）

基于神经网络关于冷却装置功率与系统总耗电量的关系模型研究

摘要

????????伴随着空调的普及，空调变得越来越不可或缺。一般的中央空调包含四大部件，压缩机、冷凝器、节流装置、蒸发器， 制冷剂 依次在上述四大部件循环，压缩机出来的冷媒（制冷剂）高温高压的气体，流经冷凝器，降温降压，冷凝器通过冷却水系统将热量带到冷却塔排出，冷媒继续流动经过节流装置，成低温低压液体，流经蒸发器，吸热，再经压缩。其中空调的冷却装置发挥了重要作用，而冷却装置功率与系统总耗电量息息相关，利用BP神经网络可以有效的建立冷却装置的功率和系统总耗电量的关系模型，从而能通过冷却装置的功率预测出系统总耗电量。

关键词：BP神经网络，冷却装置的功率，系统总耗电量

一、研究背景与意义

????????空调是一种高耗能的产品，在夏季，空调的耗电量能占到居民用电量的40%到一半左右； 在某些炎热的中东国家，夏季空调的耗电量甚至能占到居民用电量的70%。中国是世界第一大空调生产国，消费国和出口国。我国空调产量占全球产量的70%以上。随着我国的城镇化进程和人民经济水平提高，我国的居民空调持有量也不断增长。目前中国的空调持有量占全球的35%（作为比较，美国占23%）。随着气候变暖和居民经济水平提高，我国的空调持有量预计还会持续上升，与之对应的能耗压力也随之上升。研究空调的冷却装置的功率和冷却装置1的功率的关系模型，对于空调的节能研究或有重大意义。

二、解决方法及步骤

1.数据的读入和预处理

????????将测量得的中央空调的数据导入matlab中。选取研究需要的冷却装置1的功率和冷却装置2的功率这两组数据，以及系统总耗电量的相关数据。在导入的初始数据中可能含有但不属于异常值的粗大误差的数据会干扰对实验结果的分析，甚至歪曲实验结果，所以在实验中要剔除这些粗大误差，分别用std和mean函数计算出冷却装置1的功率、冷却装置2的功率和系统总耗电量的平均值和标准差，再用莱伊特准则剔除导入数据的粗大误差，根据定义进行判断，若是满足剔除条件（（数据-平均值）的绝对值>3倍标准差）就将该数据去掉；再分别读取冷却装置的功率的2*20488数据矩阵和系统总耗电量的1*20488数据矩阵。部分数据如下表1：

表1 部分数据展示

冷却装置1的功率	96.768013	96.768013	96.768013	96.256012
冷却装置2的功率	114.17601	113.664009	116.736015	115.200012
系统总耗电量	261.990784	261.766693	264.246857	263.062408

2.BP神经网络的简介和结构参数

????????BP神经网络是一种按误差反向传播 (简称误差反传)训练的多层前馈网络，其算法称为 BP算法 ，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。BP神经网络整个网络结构包含了：一层输入层，一到多层隐藏层，一层输出层。 一般说L层神经网络，指的是有L个隐层，输入层和输出层都不计算在内的。结构参数如下：

（1）隐含层层数：一般为一层，最基础实用简单计算量少；

（2）各层神经元个数：输入层和输出层有时随着系统的确定神经元个数差不多就已确定，例如电池BMS系统，如果使用BP那么输入信号一般两个（电流和电压）或者三个（电流电压温度），输出信号一般一个（SOC数值）；另外隐含层神经元个数我推荐不要少于5个；

（3）设置训练目标误差：根据系统设置，比如输出值为0-1之间的数，精度要求预测值和实际值误差在0.01以内，那目标误差理论上只要你设置小于这个误差一个数量级以下，为了尽量改善收敛效果，加大收敛力度还是目标误差设置较小一点比较恰当，不然容易提前中断训练。

（4）显示训练结果的时间间隔步数：这个跟你输入数据的时间间隔有关，训练时间间隔是输入采样时间的整数倍即可，我推荐就等于输入数据的采样时间；

（5）训练次数设置：离线情况下，训练次数要小于输入总的采样次数（总的采样次数=总的采样时间/采样时间），但训练次数又不能太小，否者造成训练不充分，训练结果没有收敛，应该是总的采样次数的后20%区间。

（6）训练允许时间，默认值INF：这个采取默认值即可；

（7）学习率，默认值为0.01：学习率和误差反向传播修正权值的步长关系很大；

3.建立研究的对象，确定输入与输出

????????在BP神经网络模型的构建中，我们从整个处理完后的冷却装置的功率数据和系统总耗电量分别选取10000个数据做为BP神经网络的训练集，再选取剩余10488个数据做为测试集，共计为20488个数据，其中输入层和输出层如表1所示。

表2 BP神经网络的输入输出

输入层	冷却装置1的功率	冷却装置2的功率
输出层	系统总耗电量

????????实验中需要将训练集样本数据进行归一化，进行归一化的目的是使得预处理的数据被限定在一定的范围内（比如 [0,1]或者 [-1,1]），从而减小奇异样本数据导致的不良影响。BP神经网络的训练集和测试集的原始数据正态概率密度分布图输出如下图：

图1 训练集的输出原始数据正态概率密度分布图

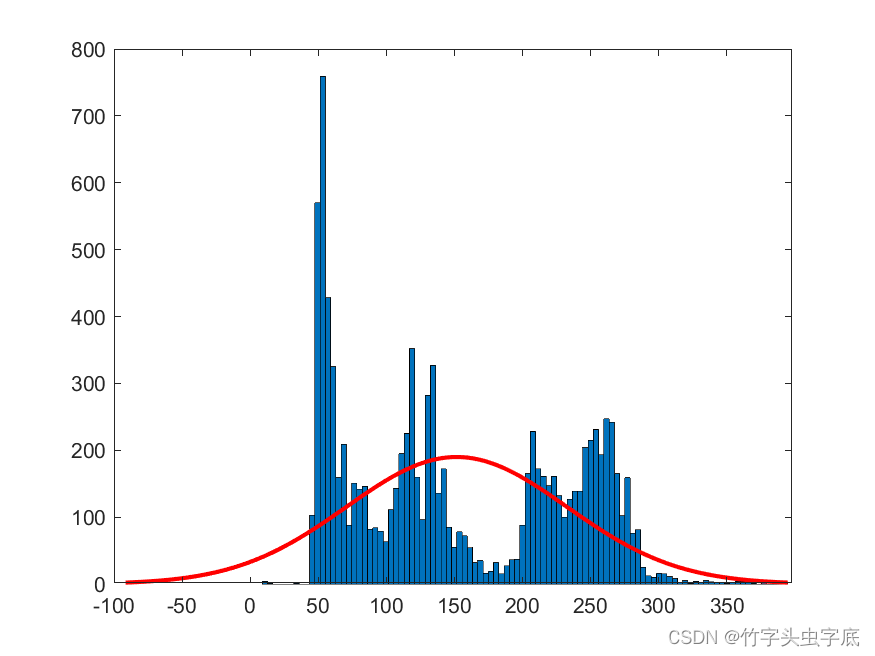
图2 测试集输出原始数据正态概率密度分布图

4.构建bp神经网络

????????实验过程中构建了一个双输入，单输出，隐含层隐含层节点数量为20个，相关层的传递函数使用默认函数，每10轮回显示一次结果；最大训练次数10000；神经网络的学习速率为0.01；训练网络所要达到的目标误差为0.0001的BP神经网络。

在程序中用到如下公式：

（平均绝对误差）

（均方误差）

?????（均方根误差）

三、实验结果与分析 ?

1.误差

????????使用训练好的BP神经网络得到的预测值与原始数据的误差如下表3，从表中可以看出当使用训练集的数据进行预测时误差和测试集计算出的预测值的误差相近，实验选取训练集数据预测出来的数据。

表3 误差

	平均绝对误差	均方误差	均方根误差	样本数
训练集	3.2069	?42.1353	?6.4912	10000
测试集	3.9535	34.8192	5.9008	10488

????????画出使用训练好的神经网络得出测试集的预测值与原始数据的误差散点图，可以看出误差集中在X轴附近。如下图3所示：

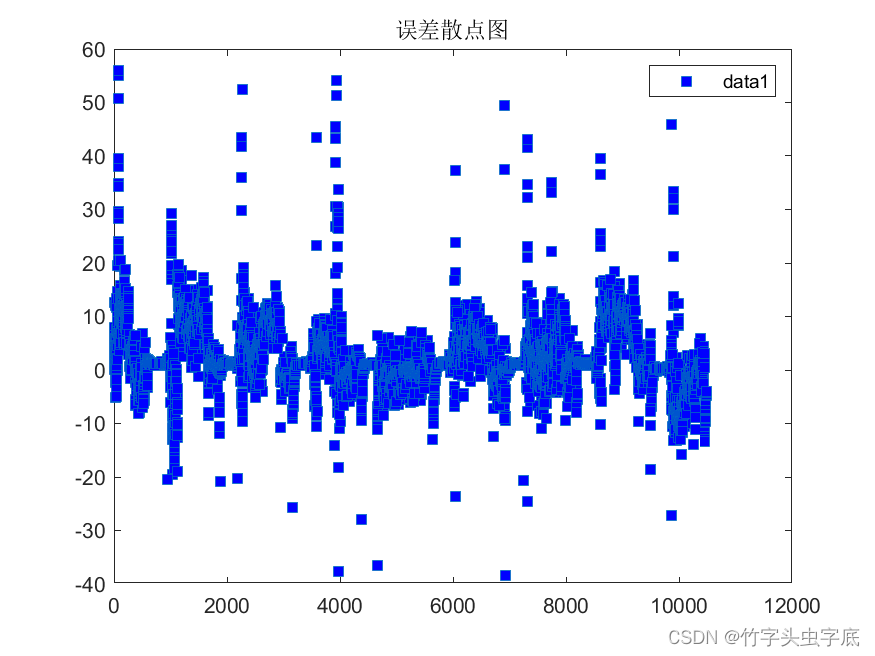
图3 误差分布散点图

如下图4为误差的误差正态概率密度分布图，可以看出多数误差都分布在-10到10之间。

图4 误差正态概率密度分布图

????????实验可以通过plot函数得出原始数据，神经网络预测数据和它们之间的误差图像，得出使用训练好的神经网络得出测试集的预测值与原始数据的BP神经网络测试集的预测值与实际值对比图，可以看出预测数据与原始数据比较接近。如下图5所示：

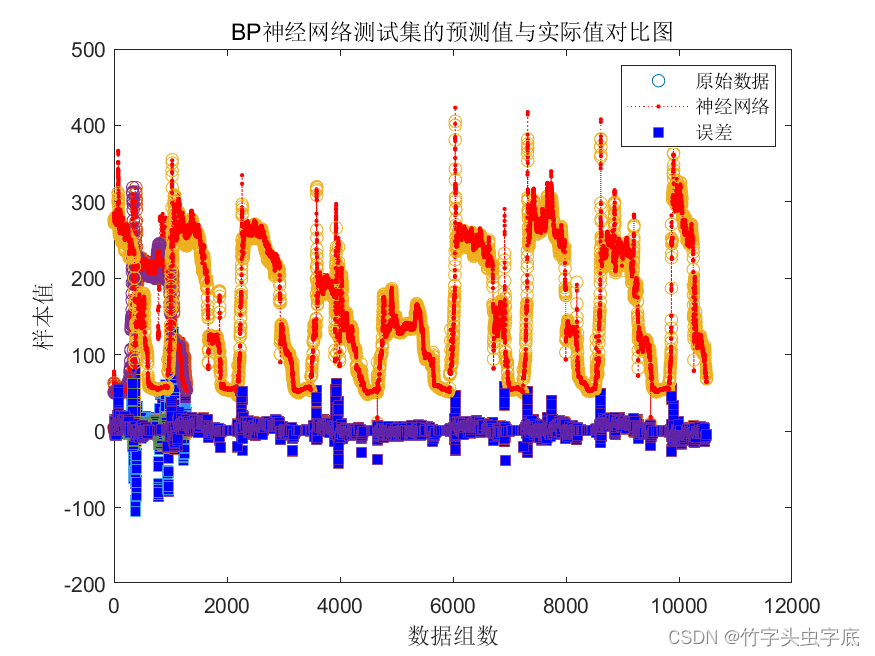
?????????????图5 BP神经网络测试集的预测值与实际值对比图

2.训练结果

????????训练性能进度如图1所示，图中有三条曲线，蓝色是训练曲线，绿色是验证曲线，红色是测试曲线，绿色的圆圈表示神经网络迭代验证终止的地方，从训练集，验证集，测试集，我们可以看到，在20代的时候就已经到达了最佳结果，均值平方差为0.0013728。此图并未表明训练有任何重大问题。验证曲线和测试曲线非常相似。如下图6所示：

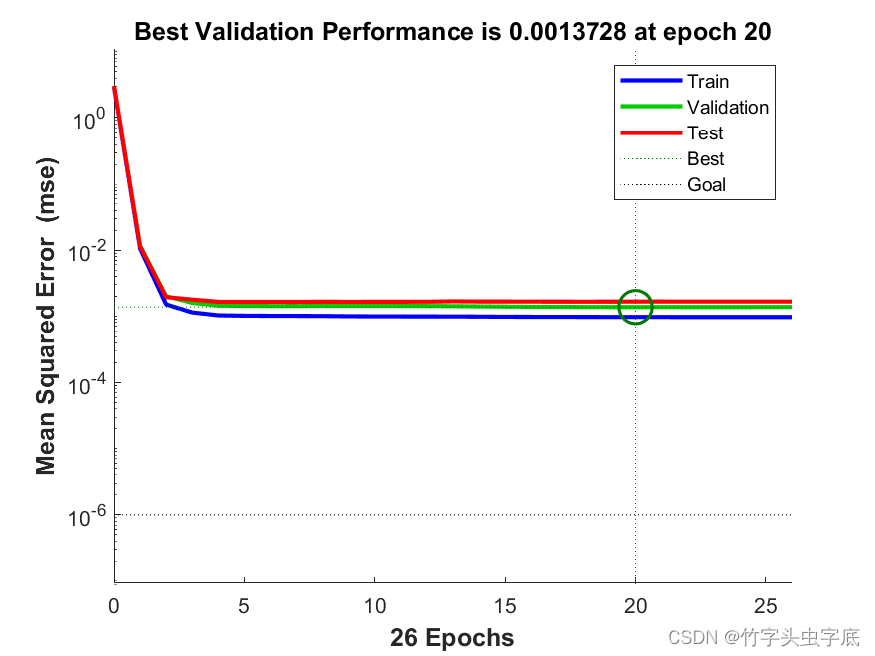
图6 性能进度图

????????在图中可以看出来，训练曲线，验证曲线，测试曲线拟合度都非常高，最后面可以看到R的拟合度达到0.99以上，拟合程度非常高，说明冷却装置的功率与系统总耗电量高度相关，由此看出冷却装置的功率可以非常好的预测出系统总耗电量。相关性如图7所示：

图7 回归图

测试集输出预测结果正态概率密度分布图如下图8所示，预测输出结果多分布在100附近和250附近。

图8 测试集输出预测结果正态概率密度分布图

代码附录：

clc

clear all

%读取数据样本的准备

A=xlsread('C:\Users\liukongyuan\Desktop\空调神经网络\B题-附件1：CACS_data_1.csv');

% cwp_pc=A(:,41);%转速%%

% chwp_pc=A(:,42);

% ct_pc=A(:,43);

XX=A(:,7:8);%X=[X1,X2,X3];程序类似用法；%转速41:43 ?%%%四个效率18:21 %%7:8是ch1-kw，ch2-kw%14:15是冷却塔

X=XX';

YY=A(:,24);%耗电量24 ??%%%系统效率27

Y=YY';

%%剔除粗大误差的代码

data=[XX,YY];

data=double(data);

for?ii = 1:3 ?%%列

????P=data(:,ii);

????ave = mean(P);%mean 求解平均值

????u = std(P);%求解标准差

????for?i = 1:20593 ??%%行

????????if(abs(P(i)-ave)>3*u)

????????????P(i) = 0;

????????????P_ans = P(P==0);

????????????len=length(P_ans);

????????????if?len == []

????????????????continue

????????????else

????????????????location=find(P==0);

????????????????if?len == 1

????????????????????loc(1,ii)=location;

????????????????else

????????????????????for?iii=1:len

????????????????????????loc(iii,ii)=location(iii);

????????????????????end

????????????????end

????????????end

????????else

????????????continue;

????????end

????end

end

ans=loc(loc~=0);

ans=unique(ans);%删除重复的值

% 根据索引去除异常值

data(ans,:)=[];

%%重新读取剔除误差的数据

X=data(:,1:2)';

Y=data(:,3)';

%准备样本数据，开始建立网络

input_train = X(:,1:10000);%4号到10号的数:1：6860

output_train =Y(:,1:10000);%训练组

input_test = X(:,10001:20488);%10月10号686:1：8142

output_test =Y(:,10001:20488);%测试组

hiddennum=20;% 隐含层节点数量

[inputn,inputps]=mapminmax(input_train);%训练样本输入归一化到[-1,1]之间

[outputn,outputps]=mapminmax(output_train);%训练样本输出归一化到[-1,1]之间

net=newff(inputn,outputn,hiddennum);% 建立模型，

net.trainParam.epochs=10000; ????????% 训练次数，这里设置为1000次

net.trainParam.lr=0.01; ??????????????????% 学习速率，这里设置为0.01

net.trainParam.goal=0.000001; ???????????????????% 训练目标最小误差，这里设置为0.00001

net=train(net,inputn,outputn);%%开始训练inputn_test=mapminmax('apply',input_test,inputps);% 对样本数据进行归一化%注释错误

inputn_test1=mapminmax('apply',input_train,inputps);% 对训练样本的输入数据进行归一化%后加的

inputn_test=mapminmax('apply',input_test,inputps);% 对测试样本的输入数据进行归一化

z=sim(net,inputn_test); %用训练好的模型进行仿真

z1=sim(net,inputn_test1); %用训练好的模型进行仿真%后加的

test_simu=mapminmax('reverse',z,outputps);%反归一化

test_simu1=mapminmax('reverse',z1,outputps);%反归一化%后加的

error=test_simu-output_test; %神经网络测试仿真结果减去测试样本中的输出结果

error1=test_simu1-output_train; %神经网络测试仿真结果减去测试样本中的输出结果%后加的

figure(1)

plot(output_test,'o');%画图；原始数据

hold on;

plot(test_simu,'r:.');%画图；神经网络算出来的数据

hold on

plot(error,'square','MarkerFaceColor','b')%误差

legend('原始数据','神经网络','误差')

xlabel('数据组数')

ylabel('样本值')

title('BP神经网络测试集的预测值与实际值对比图')

figure(2)

plot(error,'square','MarkerFaceColor','b')%误差

title('误差')

[c,a]=size(output_test);%这里的1(包括后三句)是变量，看不懂%好像是读几*几的矩阵

MAE1=sum(abs(error))/a;%平均绝对误差

MSE1=error*error'/a;%均方误差

RMSE1=MSE1^(1/2);%均方根误差

disp(['-----------------------误差计算--------------------------'])

disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下：'])

disp(['平均绝对误差为：',num2str(MAE1)])

disp(['均方误差为： ???',num2str(MSE1)])

disp(['均方根误差为： ?',num2str(RMSE1)])

MAE11=sum(abs(error1))/a;%平均绝对误差

MSE11=error1*error1'/a;%均方误差

RMSE11=MSE11^(1/2);%均方根误差

disp(['-----------------------误差计算--------------------------'])

disp(['训练隐含层节点数为',num2str(hiddennum),'时的误差结果如下：'])

disp(['训练平均绝对误差为：',num2str(MAE11)])

disp(['训练均方误差为： ???',num2str(MSE11)])

disp(['训练均方根误差为： ?',num2str(RMSE11)])

figure(3);

histfit(error);%误差频率直方图

figure(4);

histfit(test_simu);%预测模型频率直方图

figure(5);

histfit(output_test);%测试集样本输出数据频率直方图

figure(6);

histfit(input_train(1,:));%训练样本1输入数据频率直方图

figure(7);

histfit(output_train);%训练样本输出数据频率直方图

figure(8);

histfit(input_train(2,:));%训练样本2输入数据频率直方图