Lowest Common Ancestor of a Binary Search Tree
Problem
Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
According to the?definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes?p?and?q?as the lowest node in?T?that has both?p?and?q?as descendants (where we allow?a node to be a descendant of itself).”
Example 1:
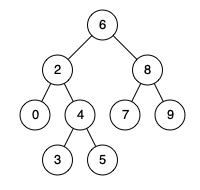
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 Output: 6 Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 Output: 2 Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [2,1], p = 2, q = 1 Output: 2
Intuition
The goal is to find the lowest common ancestor (LCA) of two given nodes in a binary search tree (BST). The intuition is to exploit the properties of a BST, where nodes in the left subtree are smaller than the root, and nodes in the right subtree are larger than the root. By comparing the values of the nodes p and q with the value of the current root, we can determine the location of the LCA.
Approach
Traversal:
Start with the root of the BST.
While traversing the tree:
If both p and q are greater than the current root's value, move to the right subtree.
If both p and q are smaller than the current root's value, move to the left subtree.
If the current root's value is between p and q, or if it is equal to either p or q, then the current root is the LCA. Return the current root.
Return Result:
Return the final result, which is the lowest common ancestor of p and q.
Complexity
- Time complexity:
The time complexity is O(h), where h is the height of the binary search tree. In the average case, for a balanced BST, the height is O(log n), making the time complexity O(log n). However, in the worst case of an unbalanced tree, the height could be O(n), resulting in a time complexity of O(n).
- Space complexity:
The space complexity is O(1) since no additional data structures are used that scale with the input size. The algorithm uses a constant amount of space to store the current root and temporary variables.
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
while root:
if root.val < p.val and root.val < q.val:
root = root.right
elif root.val > p.val and root.val > q.val:
root = root.left
else:
return root
return None本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!