[蓝桥杯学习] 倍增LCA

倍增LCA

LCA就是求公众祖先的问题

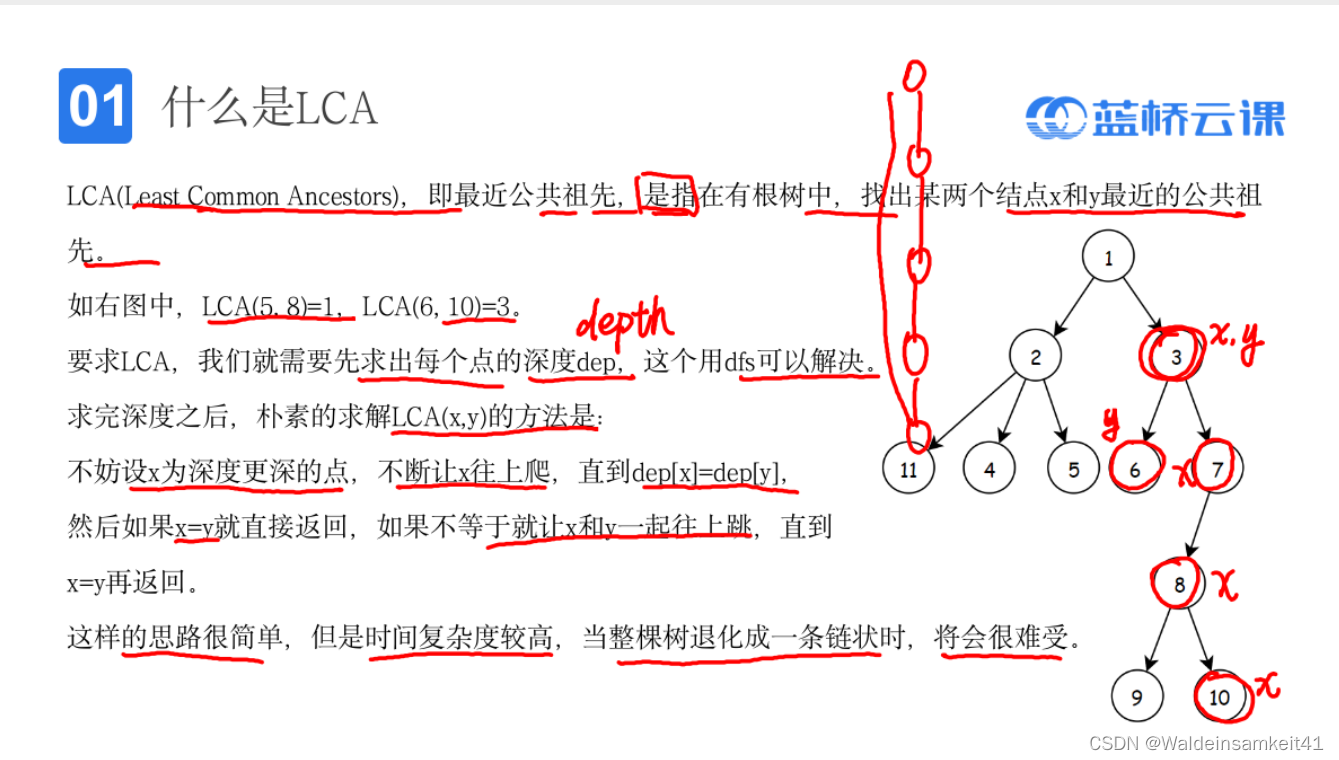
在做树的题目时，我们经常要考虑当树为一条链时的情况。

如果树较为均匀，那么我们进行操作的时间复杂度是 O(log n) ；如果一条链的话，时间复杂度变成 O(n) 如果n很大，那么此时，就会超时。

倍增法求LCA

dp 动态规划数组

fa[5][2] = fa[fa[5][1]][1] = fa[3][1] = 1

代码结构：

1. 更新dep
2. p放入fa
3. fa[x][i] = fa[fa[x][i-1]][i-1]?
4. dfs

代码结构：

1. 将x 设为深度深的那个
2. 从大到小进行for，if(dep[fa[x][i]] >= dep[y])? x = fa[x][i]? （跳8没超y就跳，超过了，就跳4，以此类推）
3. ?如果x y相同，就返回 x （这个情况是，y就是x的祖先）
4. 从大到小进行for， if(fa[x][i] != fa[y][i]) x=fa[x][i] y=fa[y][i] （为什么要保持不等：因为尽量跳远的原则，可以跳到相同的点，但是不是最近的祖先。）
5. 返回fa[x][0]

有一道简单的例题

#include <iostream>
#include<vector>
using namespace std;

const int N = 1e6;
vector<int> edge[N];  //放边
int dep[N];  //每个结点的深度
int fa[N][21];

void dfs(int t,int p)
{
  dep[t] = dep[p] + 1;
  fa[t][0]=p;
  for(int i = 1 ; i <= 20 ; i++)
  {
    fa[t][i] = fa[fa[t][i-1]][i-1];
  }
  for(const auto &v : edge[t])
  {
    if(v != p)
    {
      dfs(v,t);
    }
  }
}

int lca(int x,int y)
{
  if(dep[x] < dep[y])
  {
    swap(x,y);
  }
  for(int i = 20 ; i >= 0 ; i--)
  {
    if(dep[fa[x][i]]>=dep[y]) x = fa[x][i];
  }
  if(x==y) return x;
  for(int i = 20 ; i >=0 ; i--)
  {
    if(fa[x][i] != fa[y][i]) 
    {
      x = fa[x][i];
      y = fa[y][i];
    }
  }
  return fa[x][0];
}



int main()
{
  // 用一个fa数组保存树的结点的父亲
  // 用一个dep数组保存各个结点的深度
  int n;
  cin >> n;
  for(int i = 0 ; i < n-1 ; i++)
  {
    int u,v;
    cin >> u >> v;
    edge[u].push_back(v);
    edge[v].push_back(u);
  }
  dfs(1,0);
  int m;
  cin >> m;
  while(m--)
  {
    int x,y;
    cin >> x >> y;
    cout << lca(x,y) << '\n';
    //if(m != 1) cout << '\n';
  }


  return 0;
}