算法复杂度（时间复杂度、空间复杂度）

时间复杂度

参考：https://leetcode.cn/leetbook/read/illustration-of-algorithm/r84gmi/

1. 概念：

时间复杂度指输入数据大小为 N 时，算法运行所需花费的时间。

• 体现的是计算操作随数据大小N 变化时的变化情况。

如：

• 假设算法运行总共需要「 1 次操作」、「 100 次操作」，此两情况的时间复杂度都为常数级 O(1) ；
• 需要「 N 次操作」、「 100N 次操作」的时间复杂度都为 O(N) 。

一般情况下，算法中的基本操作语句的重复执行次数是问题规模 变量n 的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作 T(n)=Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。

T(n) 不同，但时间复杂度可能相同。 如：T(n)=n2+7n+6 与 T(n)=3n2+2n+2 它们的T(n) 不同，但时间复杂度相同，都为O(n2)。详见：下方 计算时间复杂度的计算 章节。

2. 时间频度：T(n)

• 时间频度：算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

3. 计算时间复杂度的计算

1）定理一：忽略常数项

• 若：某个程序的时间频度（即：重复执行次数）是：Tn = 2n+20

• 则：可以忽略常数项：20

• 最终：程序的时间复杂度可以是：2n

2）定理二：忽略低次项

• 若：某个程序的时间频度（即：重复执行次数）是：2n^2+3n

• 则：可以忽略变量次低的项：3n

• 最终：程序的时间复杂度可以是：2n^2

3）定理三：忽略系数

• 若：某个程序的时间频度（即：重复执行次数）是：3n^2

• 则：可以忽略变量的稀疏：3

• 最终：程序的时间复杂度可以是：n^2

注：综合上面的三个定理可以得到最终的时间复杂度O(n)

4. 常见的时间复杂度

常见的算法时间复杂度由小到大依次为：

Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜ Ο(nk) ＜Ο(2n) ;

随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低.

• 常数阶O(1)
• 对数阶O(log2n)
• 线性阶O(n)
• 线性对数阶O(nlog2n)
• 平方阶O(n^2)
• 立方阶O(n^3)
• k次方阶O(n^k)
• 指数阶O(2^n)

如图：

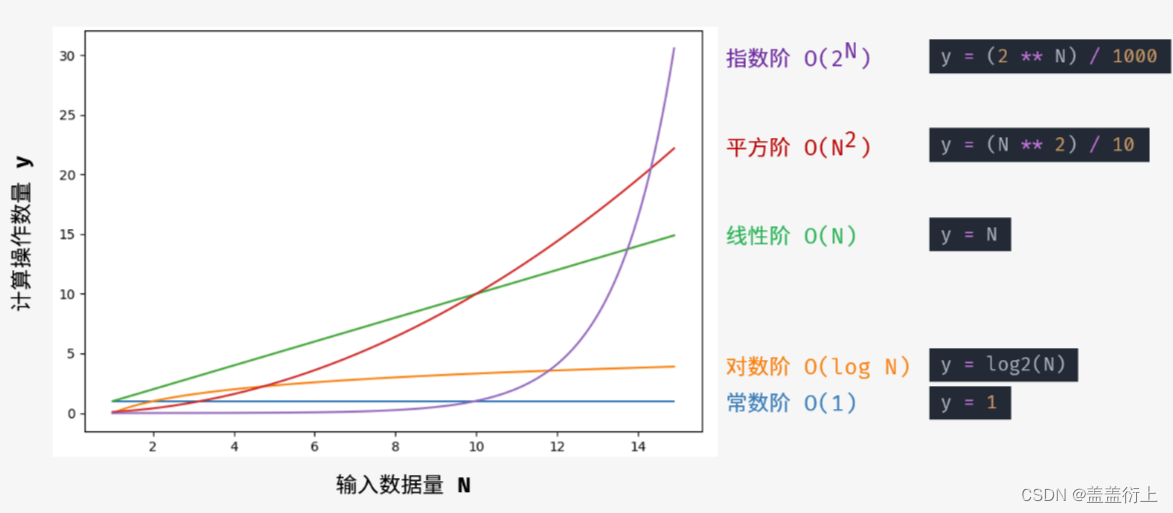
注：从图中可见，我们应该尽可能避免使用指数阶的算法

5. 平均时间复杂度和最坏时间复杂度

平均时间复杂度：

• 是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。

最坏时间复杂度：

• 最坏情况下的时间复杂度称最坏时间复杂度。

平均时间复杂度和最坏时间复杂度是否一致，和算法有关(如下图)。

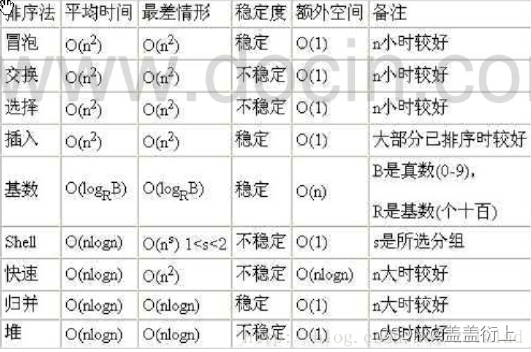
一般讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限，这就保证了算法的运行时间不会比最坏情况更长。

空间复杂度

1. 基本介绍：

• 类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间，它也是问题规模n的函数。
• 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况。
• 但是：在做算法分析时，主要讨论的是还是时间复杂度。从用户使用体验上看，更看重的是 程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间。