一篇通关代码随想录 - 二叉树

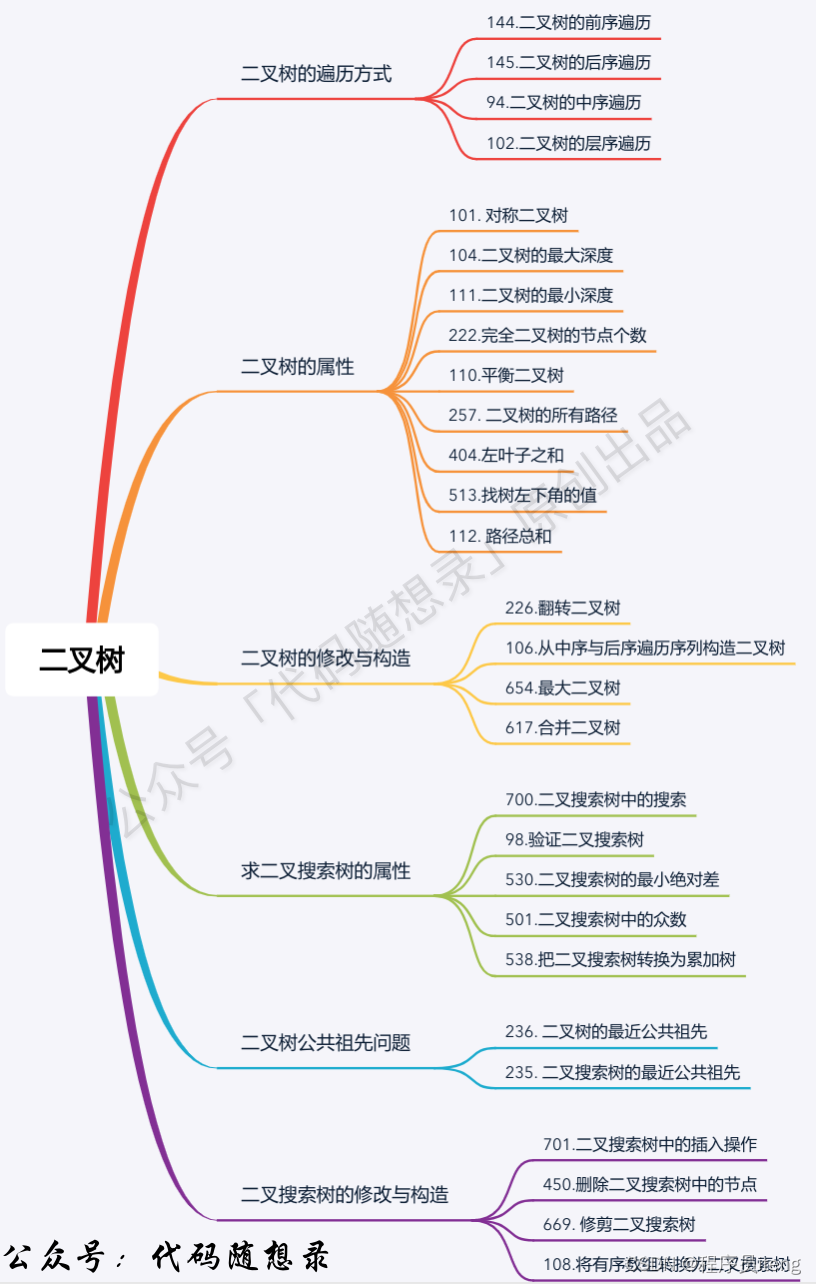
1. 二叉树的理论基础

在每一道二叉树的题目中，都可以使用递归三部曲来分析题目，看到递归，就会想：返回值、参数是什么？终止条件是什么？单层逻辑是什么？

1-1. 二叉树的种类

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

如图所示：

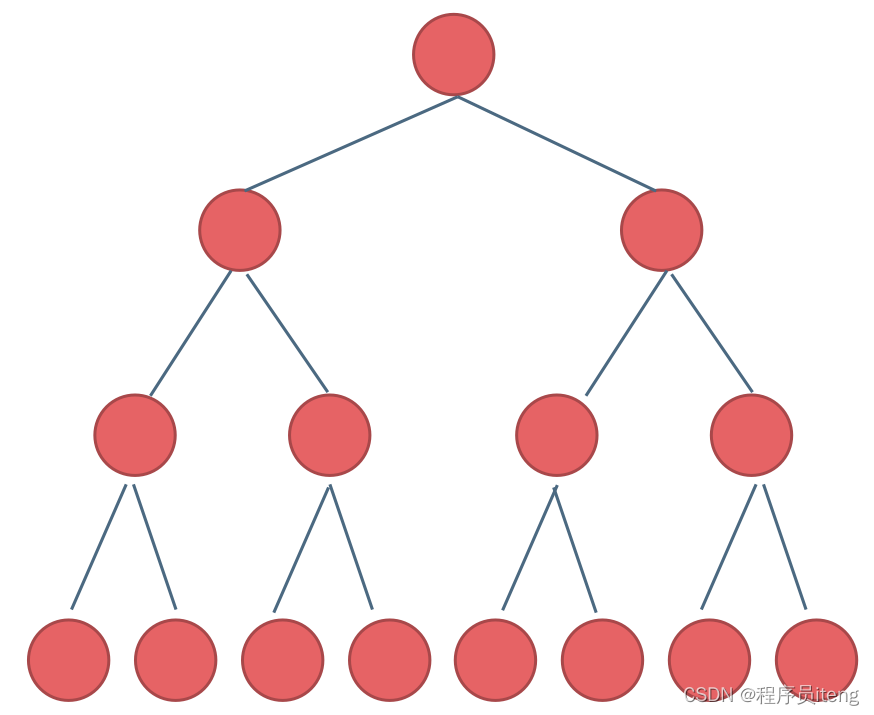
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

完全二叉树：除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

如图所示：

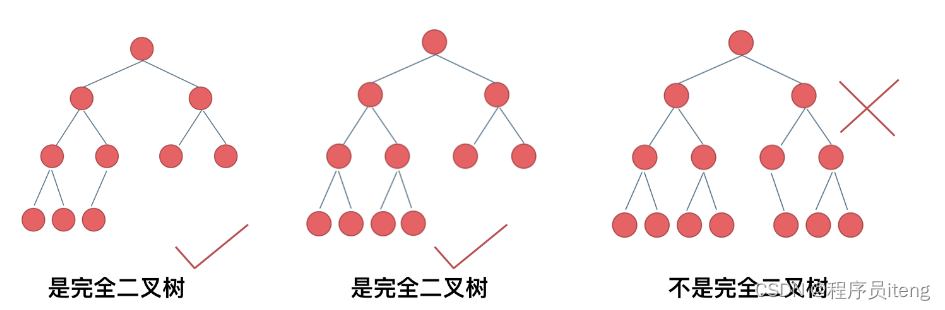
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

二叉搜索树是一个有序树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

如图所示：

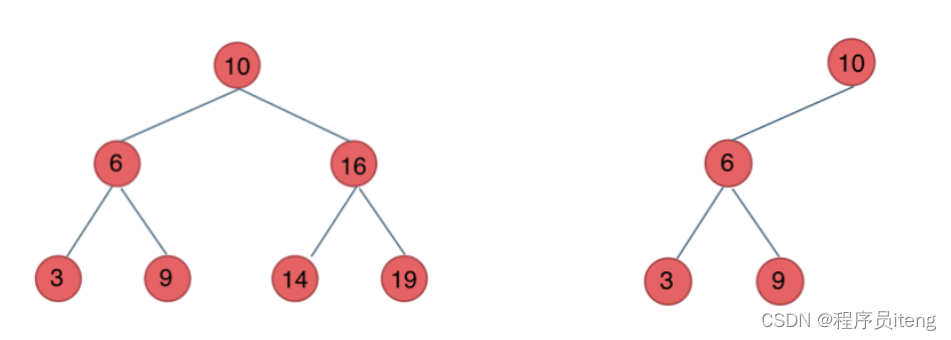
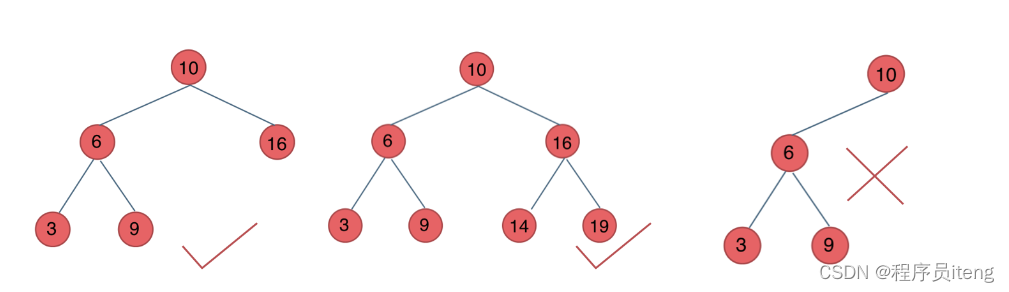
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

如图所示：

1-2. 存储方式

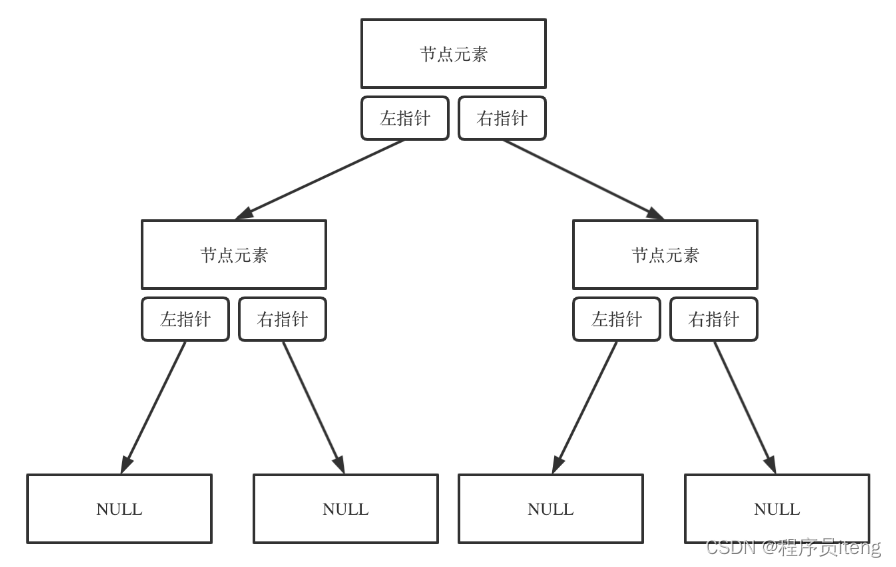
二叉树可以链式存储，也可以顺序存储。

链式存储方式就用指针， 顺序存储的方式就是用数组。

链式存储如图：

顺序存储如图：

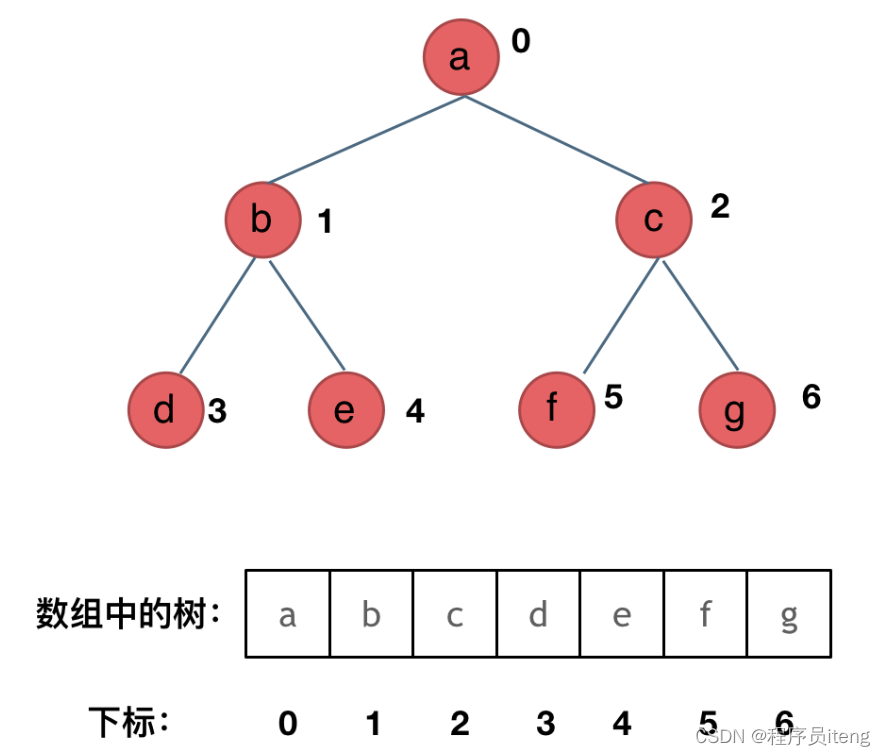
用数组来存储二叉树如何遍历:
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

1-3. 遍历方式

二叉树主要有两种遍历方式：

1. 深度优先搜索(DFS)：先往深走，遇到叶子节点再往回走。
2. 广度优先搜索(BFS)：一层一层的去遍历。

深度优先搜索

• 前序遍历（递归法，迭代法）中左右
• 中序遍历（递归法，迭代法）左中右
• 后序遍历（递归法，迭代法）左右中

广度优先搜索

• 层次遍历（迭代法）依靠队列

1-4. 定义方式

顺序存储就是用数组来存，这个定义没啥可说的，我们来看看链式存储的二叉树节点的定义方式。

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

2. 二叉树的遍历方式

2-1. 深度优先搜索

• 前中后序递归法

// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    void inorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        inorder(root.left, list);
        list.add(root.val);             // 注意这一句
        inorder(root.right, list);
    }
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postorder(root, res);
        return res;
    }

    void postorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        postorder(root.left, list);
        postorder(root.right, list);
        list.add(root.val);             // 注意这一句
    }
}

• 前中后序迭代法

2-2. 广度优先搜索

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑。

而这种层序遍历方式就是图论中的广度优先搜索，只不过我们应用在二叉树上。

// 102.二叉树的层序遍历
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        // 返回结果列表
        List<List<Integer>> res = new ArrayList();
        // 辅助队列
        Queue<TreeNode> queue = new LinkedList();
        // 如果root为空，直接返回结果列表
        if(root == null) return res;
        // 将root节点放到队列
        queue.offer(root);

        // 遍历队列中的节点
        while(!queue.isEmpty()){
            // 确定队列中还有多少个节点
            int size = queue.size();
            List<Integer> list = new ArrayList();
            // 将队列中的每个节点的子节点放到队列中
            while(size-- > 0){
                TreeNode cur = queue.poll();
                list.add(cur.val);
                if(cur.left != null) queue.offer(cur.left);
                if(cur.right != null) queue.offer(cur.right);
            }

            // 将每层的list添加到结果列表
            res.add(list);
        }

        return res;
    }
}

相似题目：

• 102.二叉树的层序遍历
• 107.二叉树的层次遍历II
• 199.二叉树的右视图
• 637.二叉树的层平均值
• 429.N叉树的层序遍历
• 515.在每个树行中找最大值
• 116.填充每个节点的下一个右侧节点指针
• 117.填充每个节点的下一个右侧节点指针II
• 104.二叉树的最大深度
• 111.二叉树的最小深度

求二叉树的属性

二叉树的修改与构造

求二叉搜索树的属性

二叉树公共祖先问题

二叉搜索树的修改与构造