【深度学习:Convolutional Neural Networks】卷积神经网络入门指南
卷积神经网络(CNN)是深度学习领域最引人注目的成就之一。自从LeCun等人在20世纪90年代初引入以来,CNN在图像处理、视频分析和自然语言处理等领域取得了显著的成就。在这篇博客中,我们将探讨CNN的基本原理、结构和一些实际应用案例。
人工智能在缩小人类与机器能力差距方面取得了巨大发展。无论是研究人员还是爱好者,都在该领域的许多方面开展工作,以实现令人惊叹的成就。计算机视觉领域就是其中之一。
人工智能在缩小人类与机器能力差距方面取得了巨大发展。无论是研究人员还是爱好者,都在该领域的许多方面开展工作,以实现令人惊叹的成就。计算机视觉领域就是其中之一。
这一领域的目标是让机器能够像人类一样观察世界,以类似的方式感知世界,甚至将知识用于图像和视频识别、图像分析和分类、媒体再创造、推荐系统、自然语言处理等多种任务。随着时间的推移,深度学习技术在计算机视觉领域的发展也日臻完善,这主要得益于一种特殊的算法–卷积神经网络。
介绍
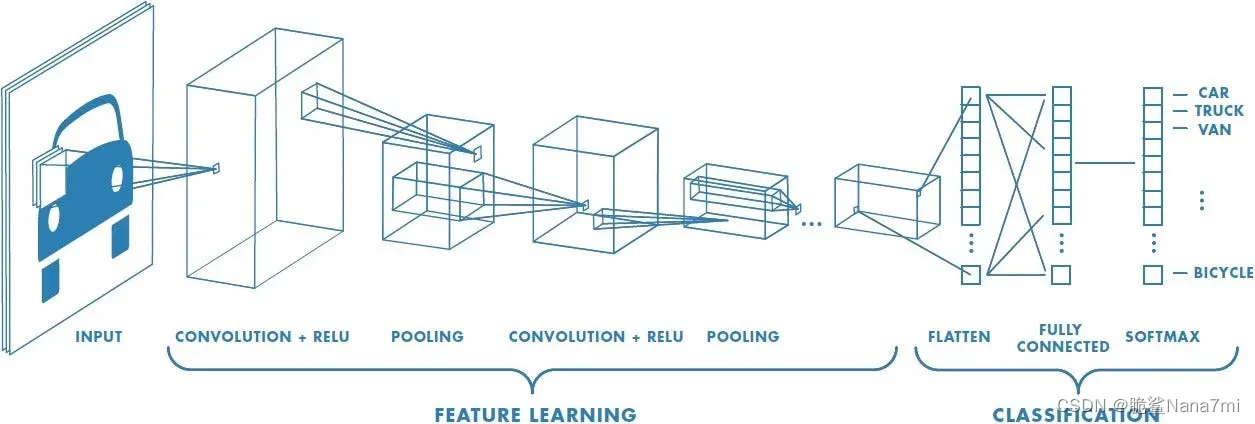
卷积神经网络 (ConvNet/CNN) 是一种深度学习算法,可以接收输入图像,为图像中的各个方面/对象分配重要性(可学习的权重和偏差),并能够区分彼此。与其他分类算法相比,ConvNet 中所需的预处理要低得多。虽然在原始方法中,过滤器是手工设计的,但经过足够的训练,ConvNets有能力学习这些过滤器/特征。
ConvNet的架构类似于人脑中神经元的连接模式,并受到视觉皮层组织的启发。单个神经元仅在视野的有限区域(称为感受野)中对刺激做出反应。此类字段的集合重叠以覆盖整个可视区域。
为什么选择ConvNets而不是前馈神经网络?

图像只不过是像素值的矩阵,对吧?那么,为什么不直接将图像展平(例如,将 3x3 图像矩阵转换为 9x1 向量)并将其馈送到多级感知器进行分类呢?呃。。没有。
在极其基本的二进制图像的情况下,该方法在执行类预测时可能会显示平均精度分数,但当涉及到具有整个像素依赖性的复杂图像时,准确性几乎没有。
ConvNet 能够通过应用相关过滤器成功捕获图像中的空间和时间依赖关系。由于涉及的参数数量的减少和权重的可重用性,该架构可以更好地拟合图像数据集。换句话说,可以训练网络以更好地理解图像的复杂程度。
Input Image 输入图像

在图中,我们有一个 RGB 图像,它被三个颜色平面(红色、绿色和蓝色)分隔开。图像存在许多这样的色彩空间——灰度、RGB、HSV、CMYK 等。
你可以想象,一旦图像达到尺寸,比如8K(7680×4320),计算量会有多大。ConvNet 的作用是将图像简化为更易于处理的形式,而不会丢失对获得良好预测至关重要的特征。当我们要设计一个不仅擅长学习特征,而且可以扩展到海量数据集的架构时,这一点很重要。
基本架构
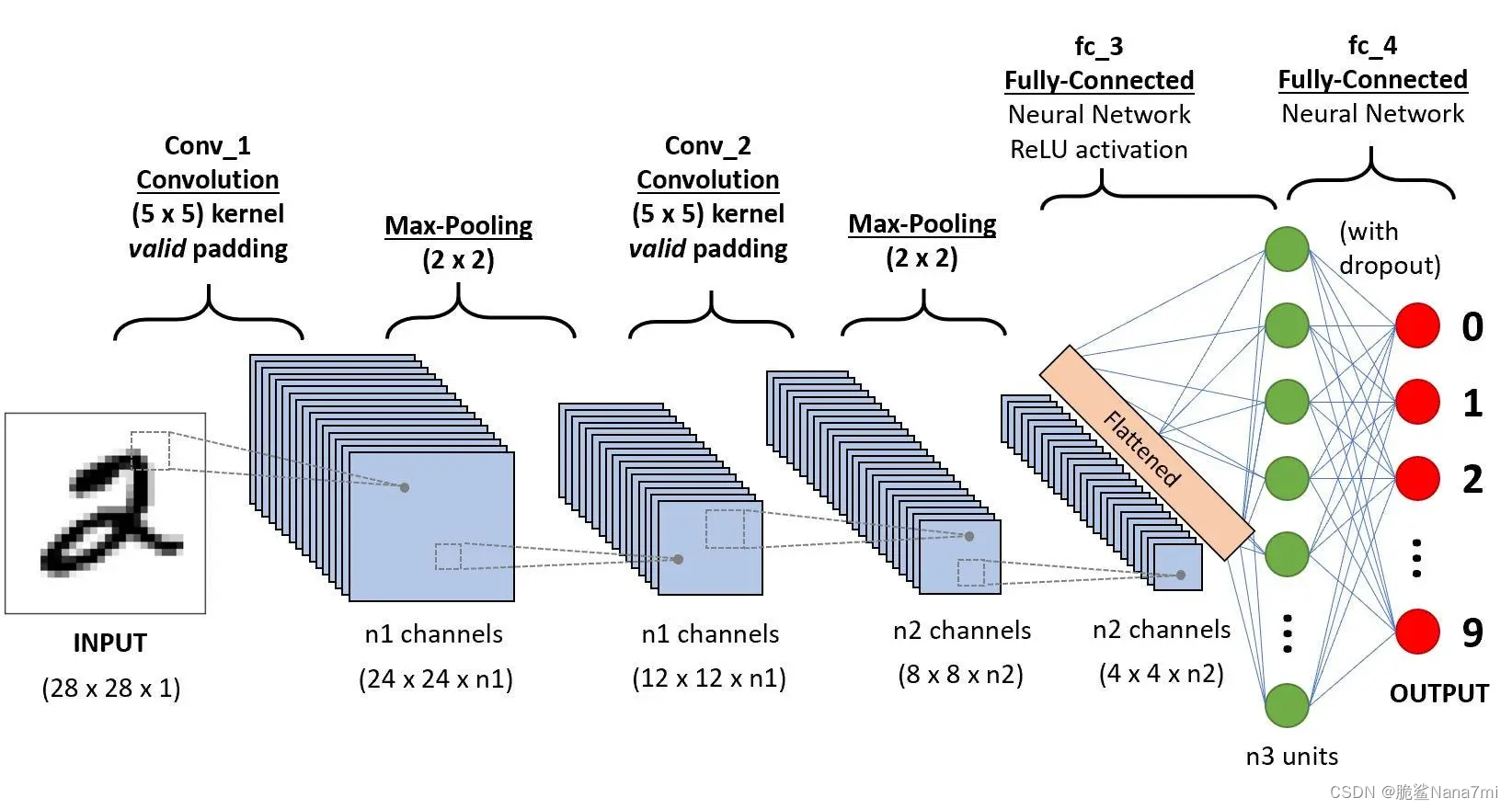
CNN主要由三种类型的层组成:卷积层、池化层和全连接层。
- 卷积层: 通过滤波器(或称为卷积核)提取输入数据(如图像)的特征。
- 池化层: 减少数据的空间大小,降低计算复杂度,同时保留重要信息。
- 全连接层: 将学习到的特征用于分类或其他任务。
Convolution Layer 卷积层 — 内核

图像尺寸 = 5(高度)x 5(宽度)x 1(通道数,例如。RGB格式)
在上面的演示中,绿色部分类似于我们的 5x5x1 输入图像 I。卷积层第一部分中卷积运算中涉及的元素称为内核/滤波器 K,以黄色表示。我们选择 K 作为 3x3x1 矩阵。
Kernel/Filter, K =
1 0 1
0 1 0
1 0 1
由于步幅长度 = 1(非步幅),内核移动 9 次,每次在 K 和内核悬停的图像部分 P 之间执行元素乘法运算(Hadamard 乘积)。

过滤器以一定的步长值向右移动,直到解析完整的宽度。继续,它以相同的步幅值跳到图像的开头(左侧),并重复该过程,直到遍历整个图像。

对于具有多个通道的图像(例如 RGB),内核具有与输入图像相同的深度。在 Kn 和 In stack ([K1, I1]; [K2, I2]; [K3, I3]) 之间执行矩阵乘法,并将所有结果与偏差相加,得到压缩的单深度通道卷积特征输出。

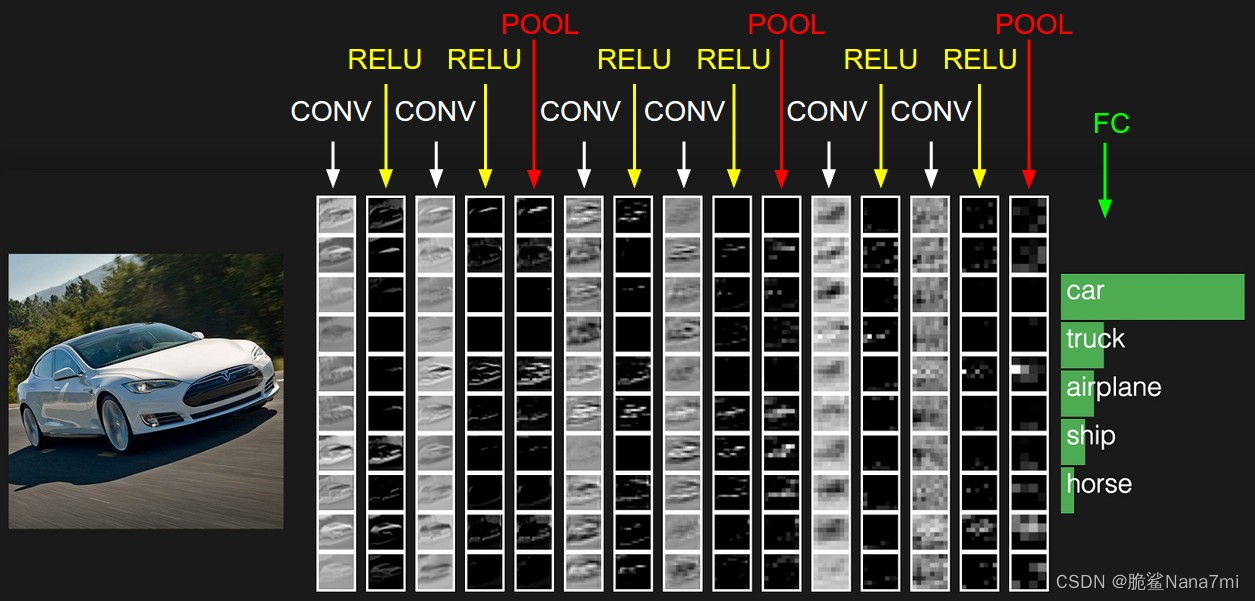
卷积运算的目的是从输入图像中提取高级特征,例如边缘。卷积网络不必仅限于一层卷积层。传统上,第一个 ConvLayer 负责捕获低级特征,例如边缘、颜色、梯度方向等。通过添加层,该架构也适应高级特征,为我们提供了一个具有全面理解的网络数据集中的图像,类似于我们的方式。
该操作有两种类型的结果 - 一种是与输入相比,卷积特征的维数减少,另一种是维数增加或保持不变。这是通过在前者的情况下应用有效填充或在后者的情况下应用相同填充来完成的。

当我们将 5x5x1 图像增强为 6x6x1 图像,然后在其上应用 3x3x1 内核时,我们发现卷积矩阵的尺寸为 5x5x1。因此得名——Same Padding。
另一方面,如果我们在没有填充的情况下执行相同的操作,我们会看到一个具有内核 (3x3x1) 本身尺寸的矩阵 - 有效填充。
下面这个链接里还有其他不同卷积的gif动画:https://github.com/vdumoulin/conv_arithmetic
Pooling Layer 池化层

与卷积层类似,池化层负责减小卷积特征的空间尺寸。这是为了通过降维来降低处理数据所需的计算能力。此外,它对于提取旋转和位置不变的主导特征很有用,从而保持有效训练模型的过程。
池化有两种类型:最大池化和平均池化。最大池化返回内核覆盖的图像部分的最大值。另一方面,平均池化返回内核覆盖的图像部分的所有值的平均值。
最大池化还可以充当噪声抑制器。它完全丢弃噪声激活,并执行去噪和降维。另一方面,平均池化只是简单地执行降维作为噪声抑制机制。因此,我们可以说最大池化的性能比平均池化要好得多。

卷积层和池化层共同构成卷积神经网络的第 i 层。根据图像的复杂性,可以增加此类层的数量以进一步捕获低级细节,但代价是更多的计算能力。
经过上述过程,我们已经成功让模型能够理解特征。接下来,我们将展平最终输出并将其输入常规神经网络以进行分类。
Classification — Fully Connected Layer (FC Layer) 分类全连接层

添加全连接层是学习卷积层输出所表示的高级特征的非线性组合的(通常)廉价方法。全连接层正在学习该空间中可能的非线性函数。
现在我们已经将输入图像转换为适合多级感知器的形式,我们将把图像展平为列向量。平坦化的输出被馈送到前馈神经网络,并将反向传播应用于训练的每次迭代。经过一系列的 epoch,该模型能够区分图像中的主要特征和某些低级特征,并使用 Softmax 分类技术对它们进行分类。
有多种可用的 CNN 架构,这些架构对于构建算法至关重要,这些算法在可预见的未来为整个人工智能提供动力。下面列出了其中一些:
- LeNet
- AlexNet
- VGGNet
- GoogLeNet
- ResNet
工作原理
CNN通过卷积层中的滤波器在输入数据上滑动,提取局部特征。这些特征随后通过网络的深层传递并逐渐集成为更高级的特征,最终用于执行诸如分类或检测的任务。
应用案例
CNN在多个领域都有广泛应用,例如:
- 图像识别: 识别图像中的物体。
- 视频分析: 追踪视频中的物体或行为。
- 自然语言处理: 虽然CNN主要用于图像,但也可以用于处理文本数据。
特征提取示例
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!