数据挖掘之贝叶斯优化——前反馈特征的参数,估计特征的最佳数值
贝叶斯优化是一个全局优化方法,用于优化具有噪声的黑盒函数。这一方法在许多现实世界的问题中都有应用,特别是在那些评估目标函数的代价很高的场合,例如超参数调优。
背景:
- 为什么需要贝叶斯优化?
在数据挖掘、机器学习和深度学习中,通常需要调整模型的参数(例如,学习率、树的深度等)来获得最佳性能。传统的方法,如网格搜索和随机搜索,不仅效率低下,而且很可能会错过最佳参数组合。而贝叶斯优化提供了一种更加高效的方法,它能够在较少的迭代中找到较好的参数值。
- 贝叶斯优化的工作原理是什么?
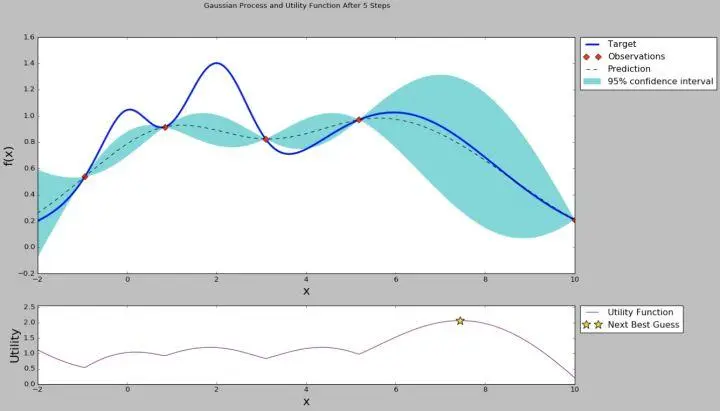
贝叶斯优化背后的核心思想是利用贝叶斯推断来构建目标函数的概率模型,通常使用高斯过程。这种概率模型能够为我们提供目标函数值的预测以及这些预测的不确定性(即预测的方差)。
基于这种预测和不确定性,贝叶斯优化定义了一个所谓的采集函数(例如预期提升),它告诉我们下一步应该在哪里评估目标函数。这样,贝叶斯优化就能够在每一步都做出明智的决策,选择合适的参数来评估,从而高效地找到最优解。
- 贝叶斯优化与特征的关系:
虽然贝叶斯优化最常用于超参数调优,但它同样可以应用于特征工程中,帮助确定最佳的特征表示或特征组合。
此外,贝叶斯优化也可以用于确定特定特征的最佳值,这在某些应用场景中可能非常有价值,例如化学、制药或其他领域,其中某些特征的精确值可能会导致最佳的实验结果。
- 前反馈特征的参数:
这通常指的是我们不仅基于模型的预测结果来更新特征的参数,还结合其他先验信息或领域知识来为优化过程提供方向。在某些场合,尤其是当数据较少或模型难以训练时,这种方法可能特别有用。
实际案例
利用贝叶斯优化来找到最优的特征值,使得模型的输出(预测的目标变量)最佳。
这是一个逆问题的实现,因为我们通常会使用特征输入模型来预测输出。但在这里,你希望固定输出,并优化输入的特征,以找到对于固定输出的最佳特征值。
import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import StandardScaler
from skopt import gp_minimize
# 假设你已经有了数据
X = np.random.rand(100000, 250)
y = np.random.rand(100000, 1)
# 数据标准化
scaler = StandardScaler().fit(X)
X_scaled = scaler.transform(X)
# 使用随机森林训练一个模型
model = RandomForestRegressor(n_estimators=100)
model.fit(X_scaled, y)
# 贝叶斯优化的目标函数
def objective_function(features):
features = np.array(features).reshape(1, -1)
prediction = model.predict(features)
# 这里我们假设目标输出为0.5(可以根据需要调整)
target_output = 0.5
return (prediction - target_output) ** 2
# 定义特征的范围(因为我们进行了标准化,所以大部分值都在-3到3之间)
dimensions = [(-3.0, 3.0) for _ in range(250)]
# 使用贝叶斯优化
res = gp_minimize(objective_function, dimensions, n_calls=50, random_state=0)
# 获取最佳特征值,并转换回原始尺度
best_features_scaled = res.x
best_features = scaler.inverse_transform(np.array(best_features_scaled).reshape(1, -1))
print(best_features)
在上面的代码中,我们首先对数据进行了标准化处理,并用标准化后的数据训练了一个随机森林模型。然后,我们定义了一个目标函数,它接受一组特征作为输入,计算模型的预测输出,并返回该预测输出与我们期望的目标输出之间的差异。最后,我们使用gp_minimize进行贝叶斯优化,试图找到最小化该差异的特征值。
当我们使用StandardScaler进行标准化时,我们实际上是对每个特征执行以下操作:
- 从每个特征中减去其均值。
- 将结果除以特征的标准差。
这样处理后,每个特征的均值为0,标准差为1。在正态分布的假设下,约99.7%的数据会落在均值(也就是0)的3个标准差范围内,因此范围从-3到3包括了绝大部分的数据。
实际上,不所有的特征都会严格遵循正态分布,但这是一个常用的假设,特别是在缺乏其他特定信息的情况下。如果你知道某些特征的分布不是正态分布,或者有异常值,那么可能需要为这些特征设置不同的范围。
在这个示例中,我们使用(-3, 3)作为标准化后特征的默认范围,主要是为了简化和方便。在实际应用中,你可能需要根据实际数据的分布情况来调整这个范围。
当我们使用StandardScaler对数据进行标准化时,我们的目的是使每个特征的均值为0,标准差为1。这意味着,对于标准正态分布的数据:
大约68%的数据点会落在均值的±1个标准差内(即,范围[-1, 1])
大约95%的数据点会落在均值的±2个标准差内(即,范围[-2,2])
大约99.7%的数据点会落在均值的±3个标准差内(即,范围[-3, 3])
因此,选取范围[-3, 3]是基于标准正态分布的这个特性。它意味着我们认为99.7%的标准化后的数据点都应该落在这个范围内。
但是,必须注意的是,不是所有的数据都会严格遵循正态分布。实际上,数据的真实分布可能会有所偏差。在这种情况下,可以采取以下几种策略来确定范围:
-
数据观察:你可以观察数据的实际分布,例如使用直方图或密度图,并根据观察来调整范围。
-
百分位:使用数据的百分位数来确定范围。例如,可以选择1%和99%的百分位数作为范围的下限和上限,确保覆盖大部分数据。
-
试错法:开始时可以使用[-3, 3],但根据贝叶斯优化的结果和收敛性,逐步调整范围。
-
领域知识:如果你对数据有深入的了解,或者你知道某些特征的物理、生物或经济上的限制,可以利用这些知识来设定范围。
这一类数据的应用场景,就是当我们有大量的数据是正常的,也是比较好的数据之后,我们可以收集好数据集,并将数据的质量提高
其次就是建立基础的模型
通过目标优化函数和目标优化变量,并返回特征数值的最佳值应该是哪些?
Optimized Parameters (scaled):
[0.56, 0.12, -0.34, …, 0.71, 0.92, -0.65]
Optimized Parameters (original scale): [12.45, 50.32, 120.23, …,
23.89, 450.32, 98.21]
这一类问题解决的前提就是:
- 首先我们有大量的数据
- 其次就是优质的数据源
- 好的生产数据,用于模型的学习
- 强大的计算资源
通过拿到问题我们都是采取机器学习的一些相关的回归算法进行,不管是神经网络模型还是各种基于概率还是树的模型,多个特征去预测一个特征是符合也是比较常见的一种建模思想,但是随着机器学习和深度学习的不断衍生,我们的需求也在越来越明确。
如果可以通过建立一个好的模型来调节和反馈我们实际生产过程中的哪些参数,对于我们“去中心化”,有着很好的帮助。
传统的制造业或者实际厂家都是结合经验和数据进行,可能一个工艺表一直在沿用,但是随着设备和不同情况的更新迭代与出现,这种只依靠经验的规则无法适用于大规模的数据,一个工序只能一个人来调节,多个工序可能需要多个工艺师来互相配合,无法达到最优的结果。
每文一语
不要只停留在当前的技术,要不断的去更新和迭代自己的思想
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!