希尔伯特黄变换(hht)
2023-12-16 05:12:21
提示:主要对希尔伯特黄变换进行简略的介绍
一、希尔伯特黄变换是什么?
1.1 定义
为了纪念故事中两位老先生(Hilbert和Huang)的突出贡献,人们决定把“经过EMD分解出的IMF分量再经过Hilbert变换,最终得到信号瞬时频率和瞬时幅值”的方法叫做希尔伯特黄变换
来源链接
1.2 公式
a(t):瞬时幅值

图片链接
二、代码
2.1.代码
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from pyhht import EMD
from scipy.signal import hilbert
import tftb.processing
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
matplotlib.rcParams['axes.unicode_minus'] = False # 显示负号
def picture(x, y, N):
'''
画信号的时域图和频谱
输入:
x: 0-1时间序列
y: 信号
N: 1s内采样点数
输出:
信号的时域图和频谱
'''
ax1 = plt.subplot(2, 1, 1)
plt.plot(x, y)
plt.xlabel('时间/s')
plt.ylabel('幅值')
plt.title('合成信号时域曲线')
yf = np.fft.fft(y)
xf = np.linspace(0.0, N / 2, N // 2)
ax2 = plt.subplot(2, 1, 2)
plt.plot(xf, 2.0 / N * np.abs(yf[:N // 2])) # 频谱幅值归一化,需要*2/N
plt.xlabel('频率/Hz')
plt.ylabel('幅值')
plt.title('合成信号频谱')
plt.show()
def HHTAnalysis(t, signal, N):
'''
进行HHT分析,画出每一个IMF的时域图和频谱
输入:
t: 0-1时间序列
signal: 信号
N: 1s内采样点数
输出:
信号每一个IMF的时域图和频谱
且返回IMFs,维度为(IMFs个数,信号点数N)
'''
# 进行EMD分解
decomposer = EMD(signal)
# 获取EMD分解后的IMF成分
imfs = decomposer.decompose()
# 分解后的IMF个数
n_components = imfs.shape[0]
# 画出每一个IMF的时域图和频谱
fig1, axes = plt.subplots(n_components, 2, figsize=(10, 7), sharex='col', sharey=False)
for i in range(n_components):
# 画时域图
axes[i][0].plot(t, imfs[i])
axes[i][0].set_title('IMF{}'.format(i + 1))
# 画fft图
yf = np.fft.fft(imfs[i])
xf = np.linspace(0.0, N / 2, N // 2)
axes[i][1].plot(xf, 2.0 / N * np.abs(yf[:N // 2])) # 频谱幅值归一化,需要*2/N
axes[i][1].set_title('IMF{}'.format(i + 1))
plt.show()
return imfs
def HHTPicture(t, imfs, N, n):
'''
画出指定个数的IMFs的时域图和时频图
输入:
t: 0-1时间序列
imfs: IMFs成分
N: 1s内采样点数
n: 指定画前几个IMFs成分
输出:
前n个IMFs的时域图和时频图
'''
fig2, axes = plt.subplots(n, 2, figsize=(10, 7), sharex='col', sharey=False)
# 计算并绘制各个组分
for iter in range(n):
# 绘制分解后的IMF时域图
axes[iter][0].plot(t, imfs[iter])
axes[iter][0].set_xlabel('时间/s')
axes[iter][0].set_ylabel('幅值')
# 计算各组分的Hilbert变换
imfsHT = hilbert(imfs[iter])
# 计算各组分Hilbert变换后的瞬时频率
# 使用梯形积分法计算解析信号在特定时间瞬时的瞬时频率。
instf, timestamps = tftb.processing.inst_freq(imfsHT)
# 绘制瞬时频率,这里乘以fs是正则化频率到真实频率的转换
# plt.figure(figsize=(10, 7))
# plt.plot(timestamps, instf)
# # 绘制标题
# plt.title('hilbert')
fs = N
axes[iter][1].plot(timestamps / fs, instf * fs)
axes[iter][1].set_xlabel('时间/s')
axes[iter][1].set_ylabel('频率/Hz')
# 计算瞬时频率的均值和中位数
axes[iter][1].set_title(
'Freq_Mean{:.2f}----Freq_Median{:.2f}'.format(np.mean(instf * fs), np.median(instf * fs)))
def HHTFilter(signal, componentsRetain):
'''
定义HHT的滤波函数,提取部分EMD组分
输入:
signol: 信号
componentsRetain: IMF的列表 []
输出:
一幅图,同时包含原始信号和合成信号
'''
# 进行EMD分解
decomposer = EMD(signal)
# 获取EMD分解后的IMF成分
imfs = decomposer.decompose()
# 选取需要保留的EMD组分,并且将其合成信号
signalRetain = np.sum(imfs[componentsRetain], axis=0)
# 绘图
plt.figure(figsize=(10, 7))
# 绘制原始数据
plt.plot(signal, label='RawData')
# 绘制保留组分合成的数据
plt.plot(signalRetain, label='HHTData')
# 绘制标题
plt.title('RawData-----HHTData')
# 绘制图例
plt.legend()
plt.show()
return signalRetain
# 生成0-1时间序列,共2048个点
N = 2000
t = np.linspace(0, 1, N)
# 生成信号
# signal = (2 + np.cos(8 * np.pi * t)) * np.cos(40 * np.pi * (t + 1) ** 2) + np.cos(
# 20 * np.pi * t + 5 * np.sin(200 * np.pi * t))
signal = 0.8 * np.cos(20 * np.pi * t*2) + 0.5 * np.cos(40 * np.pi * (t + 1) * 2) + 0.2*np.cos(
200 * np.pi * t*2) + 0.1 * np.cos(400 * np.pi * t*2)
# 画出原始信号的时域图和频谱
picture(t, signal, N)
# 进行HHT分析,画出所有IMFs的时域图和频谱
imfs = HHTAnalysis(t, signal, N)
# 画出前2个IMFs的时域图和时频图
HHTPicture(t, imfs, N, 4)
# 为了纪念故事中两位老先生(Hilbert和Huang)的突出贡献,人们决定把“经过EMD分解出的IMF分量再经过Hilbert变换,最终得到信号瞬时频率和瞬时幅值”的方法叫做希尔伯特黄变换
# 进行验证,判断与原始信号的差异
signalRetain = HHTFilter(signal, [0, 1])
2.2 结果分析
2.2.1 第一张图
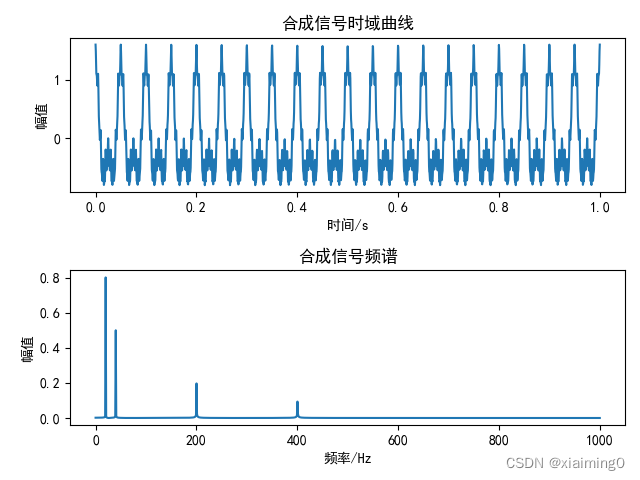
上图:合成的原始信号(频率分别为20Hz,40Hz,200Hz,400Hz的正弦波)。
下图:合成的原始图像的频谱,频率成分明显。
2.2.2 第二张图
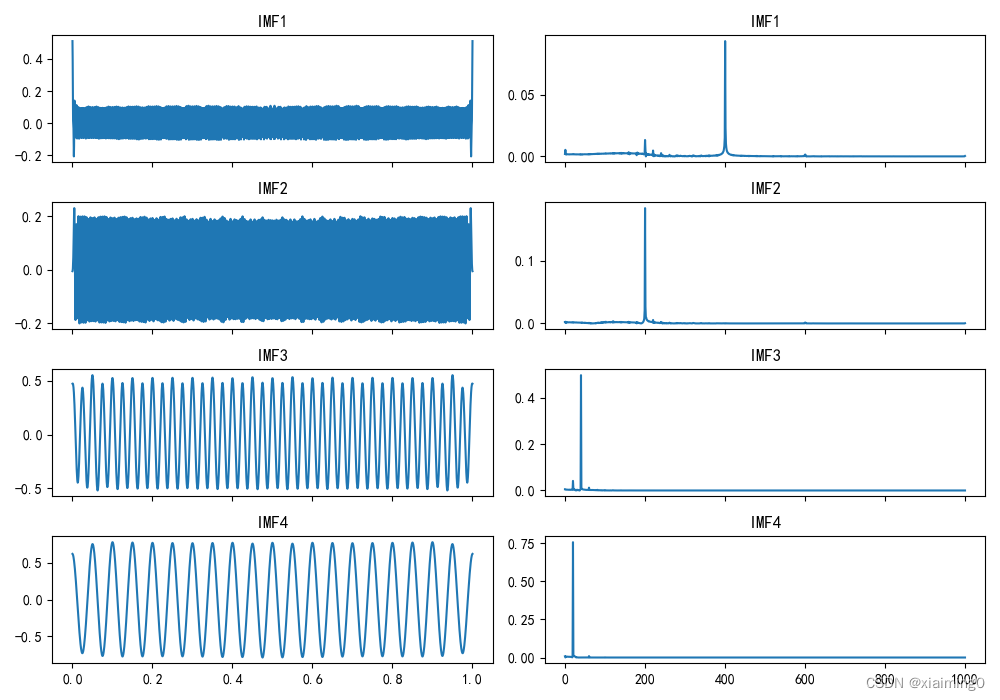
对原始振动信号进行EMD分解,只显示前4个IMF分量。
左侧是EMD分解后得到的原始图像,左侧是对右侧图像分别进行FFT(快速傅里叶变换)后的图像。(IMF1主要频率成分400Hz,IMF2主要频率成分200Hz,IMF3主要频率成分40Hz,IMF3主要频率成分20Hz)
2.2.3 第三张图
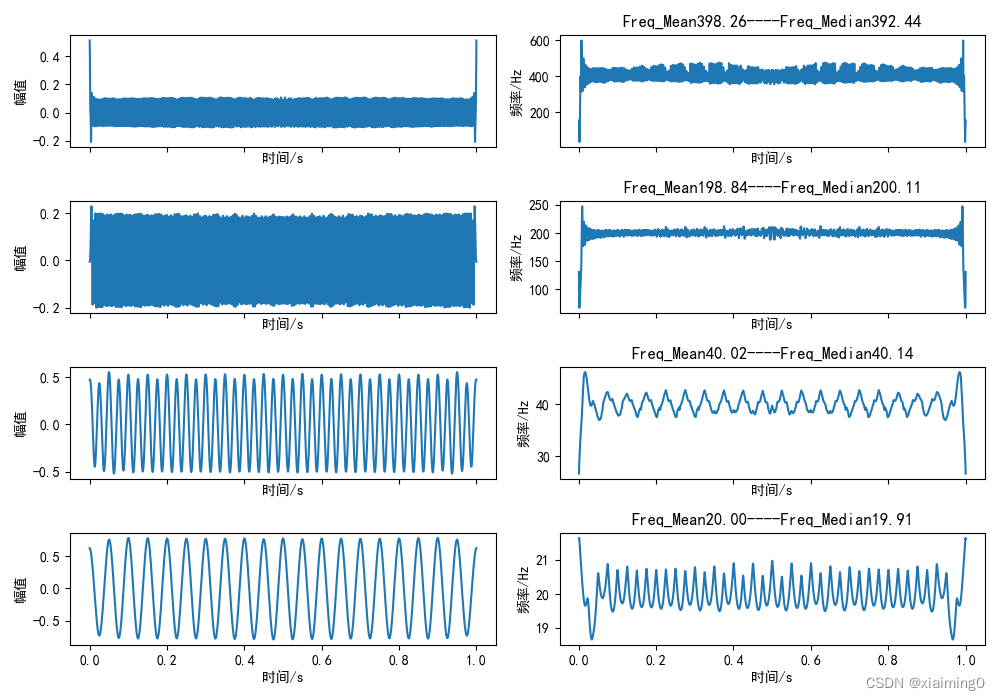
左侧是EMD分解后得到的原始图像,左侧是对右侧图像分别先进行Hilbert变换,再进行瞬时频率计算得到的结果。
左侧可以显示不同IMF分量在不同时刻的频率成分。
总结
希尔伯特黄变换是一种时频分析手段,对于分稳态信号的分析较有效。
文章来源:https://blog.csdn.net/xiaiming0/article/details/135024547
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!