数据结构和算法:二分法
2023-12-27 19:40:50
文章目录
一:最基本的二分法
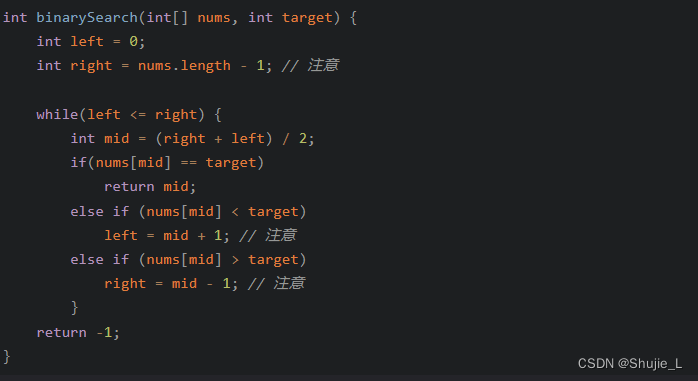
使用else if收缩空间,思路更清晰
不要出现搜寻空间不要使用else,而是使用else if,把所有的条件都写得清清楚楚,理解更清晰
防止数据太大溢出int的范围
mid = left + (right - left )/2
优化:mid = left + (right - left ) >> 1 ,位移运算,效率更高
什么情况使用while(left <= right)?为什么这个时候right = nums.length - 1?
1.左闭右闭的时候,即搜索区间是[left,right]。终止条件是区间等于[left,left - 1]的时候。
例如[1,1]这个区间还有意义,还要搜索一次。但是[0,1]这个区间没有意义了,可以停止搜索了
2.因为搜索区间是[left,right],right边界可以等于后一个元素的索引。假如right = nums.length的话就越界了
什么情况使用while(left < right)?为什么这个时候right = nums.length?
1.因为这个时候是左闭右开搜索区间,即搜索区间是[left,right),终止条件是left == right,因为[1,1)是没有意义的,可以停止搜索了。
2.因为搜索区间是[left,right),right边界不包含最后一个元素的,所以right搜索边界要比最后一个元素下标+1.
缺陷
无法查找有序数组中目标值的左右边界
二:存在重复元素,寻找左边界的二分查找
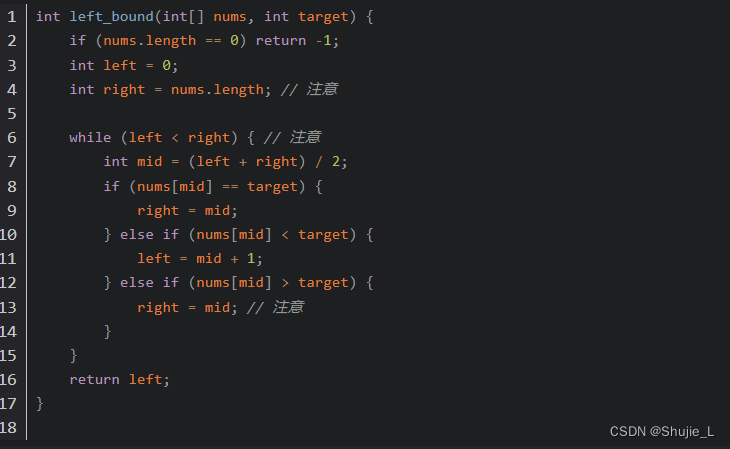
锁定target,收缩右边界的时候使用:right = mid
如果不存在target的时候怎么处理?
假如在nums = {2,3,5,7},target = 1,那么算法返回0,
假如target=8,会返回4.
加个判断:return nums[left] == target ? left : -1;
运行结果:
找到重复target的左边界:
范围内,存在 1
范围内,不存在 2
范围左边,不存在 0
范围右边,不存在 4
三:存在重复元素,寻找右边界的二分查找
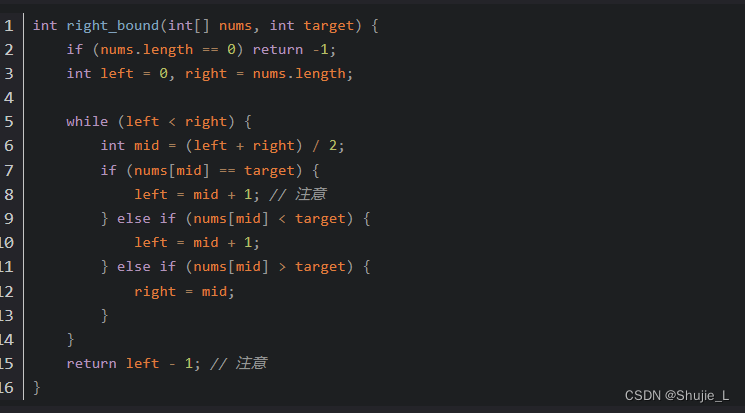
锁定target,收缩左边界的时候使用:left = mid + 1,最后一次收缩会导致下标+1,所以最后需要left - 1。
假如在nums = {2,3,5,7},target = 1,那么算法返回-1,
假如target=8,会返回3.
运行结果:
找到重复target的右边界:
范围内,存在 1
范围内,不存在 1
范围左边,不存在 -1
范围右边,不存在 3
添加边界处理条件
//因为是通过 left = mid + 1进行收缩右边界,所以最后的时候一定会往后多移动了一位下标。
int bound = left - 1;
//假如找不到右边界,
if (bound == -1) return -1;
/* return left - 1;*/
return nums[bound] == target ? bound : -1;
文章来源:https://blog.csdn.net/Shujie_L/article/details/135252614
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!