代码随想录1月9日平衡二叉树、二叉树的所有路径
110.平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点?的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
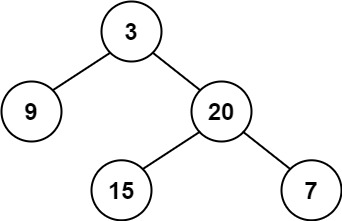
输入:root = [3,9,20,null,null,15,7] 输出:true
示例 2:
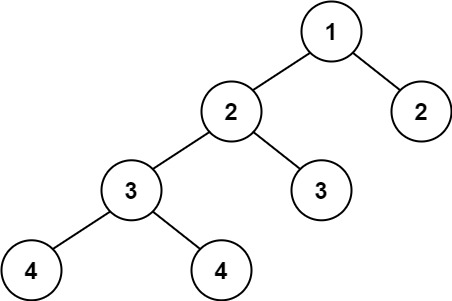
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
示例 3:
输入:root = [] 输出:true
提示:
- 树中的节点数在范围?
[0, 5000]?内 -104 <= Node.val <= 104
思路
上一道题目刚写了递归计算当前树的最大深度,所以我们可以用来判断当前节点左右子树高度是否满足平衡二叉树的要求。
我从根节点开始判断,一层一层往下走,所以是自顶向下的解法,首先判断左子树与右子树高度相差是否小于等于1,若不是直接返回false,是的话继续向下一层递归。
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null){
return true;
}
if(Math.abs(countLevel(root.left)-countLevel(root.right))<=1){
return isBalanced(root.left)&&isBalanced(root.right);
}
}
public int countLevel(TreeNode root){
if(root==null){
return 0;
}
return Math.max(countLevel(root.left),countLevel(root.right))+1;
}
}但是这样的解法虽然很直观,但是会发现countlevel调用的次数有点过多了,对于同一个节点,会重复调用,这导致时间复杂度有o(n2),我们可以换用自底向上的方法,减少调用的次数。
自底向上递归的做法类似于后序遍历,对于当前遍历到的节点,先递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的,则返回其高度(高度一定是非负整数),否则返回 ?1。如果存在一棵子树不平衡,则整个二叉树一定不平衡。
class Solution {
public boolean isBalanced(TreeNode root) {
return countLevel(root)>=0;
}
public int countLevel(TreeNode root){
if(root==null){
return 0;
}
int leftLevel=countLevel(root.left);
int rightLevel=countLevel(root.right);
if(leftLevel==-1||rightLevel==-1||Math.abs(leftLevel-rightLevel)>1){
return -1;
}else{
return Math.max(leftLevel,rightLevel)+1;
}
}
}257.二叉树的所有路径
给你一个二叉树的根节点?root?,按?任意顺序?,返回所有从根节点到叶子节点的路径。
叶子节点?是指没有子节点的节点。
?
示例 1:
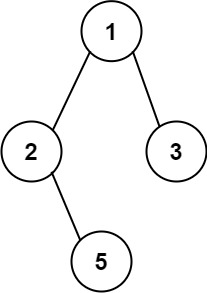
输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
提示:
- 树中节点的数目在范围?
[1, 100]?内 -100 <= Node.val <= 100
思路
之前基本没有接触过回溯的思想,一下子不知道怎么做,但其实递归和回溯思想密切相关,这里我们可以使用深度优先搜索法,每次碰到非叶子节点就分别递归左右节点,这个时候把之前存储的路径作为新递归的输入,相当于一个回溯的存档,左边节点的路径不会影响右边节点路径的记录。
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths=new ArrayList<String>();
constructPaths(root,"",paths);
return paths;
}
public void constructPaths(TreeNode root,String path,List<String> paths){
if(root!=null){
StringBuffer pathSB=new StringBuffer(path);
pathSB.append(Integer.toString(root.val));
if(root.left==null&&root.right==null) { //当前节点为叶子节点
paths.add(pathSB.toString());
}else{
pathSB.append("->");
constructPaths(root.left,pathSB.toString(),paths);
constructPaths(root.right,pathSB.toString(),paths);
}
}
}
}在java中使用StringBuffer灵活构造字符串。
题解中还有一种方法使用的是广度优先搜索法。思路也是回溯法,和递归法的回溯不同的是它把存档点放在了队首。
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
if (root == null) {
return paths;
}
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<String> pathQueue = new LinkedList<String>();
nodeQueue.offer(root);
pathQueue.offer(Integer.toString(root.val));
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.poll();
String path = pathQueue.poll();
if (node.left == null && node.right == null) {
paths.add(path);
} else {
if (node.left != null) {
nodeQueue.offer(node.left);
pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString());
}
if (node.right != null) {
nodeQueue.offer(node.right);
pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString());
}
}
}
return paths;
}
}
总结
递归思想越来越熟练,但是有些地方的优化还需要注意一下。
第二题是第一次正式接触回溯法,理解了思路之后感觉也不是很难了。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!