【FPGA】Verilog 实践：优先级编码器 | Priority encoder

---

0x00 优先级编码器（Priority encoder）

"能将多个二进制输入压缩成更少数目输出的电路或算法的编码器"

优先级编码器是一种编码器，它考虑了两个或更多输入位同时变为 1 但没有收到输入的情况。当输入进来时，优先级编码器会按照优先级顺序进行处理。

通常，它按升序或降序排列输入的优先级，当没有输入时，它会向 ?输出一个 1，以区分零输入和零输出。在下面的真值表中，输入值的优先级顺序如下：

优先级编码器
0	1	2	3	X	Y	NR
0	0	0	0	X	X	1
1	0	0	0	0	0	0
X	1	0	0	0	1	0
X	X	1	0	1	0	0
X	X	X	1	1	1	0

0x01 实现优先级编码器

为优先级编码器构建一个逻辑电路，使得该电路适用于所有输入形式 (16种)，而不仅仅是 4 到?2 编码器的 4 种形式。

0x02 真值表

输入				输出
A	B	C	D	E0	E1	NR
0	0	0	0	X	X	1
0	0	0	1	1	1	0
0	0	1	0	1	0	0
0	0	1	1	1	1	0
0	1	0	0	0	1	0
0	1	0	1	1	1	0
0	1	1	0	1	0	0
0	1	1	1	1	1	0
1	0	0	0	0	0	0
1	0	0	1	1	1	0
1	0	1	0	1	0	0
1	0	1	1	1	1	0
1	1	0	0	0	1	0
1	1	0	1	1	1	0
1	1	1	0	1	0	0
1	1	1	1	1	1	0

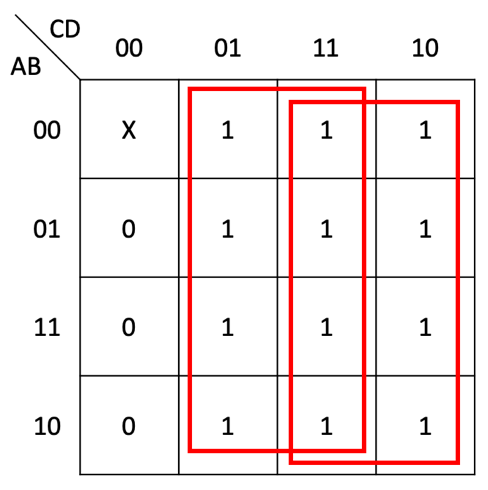
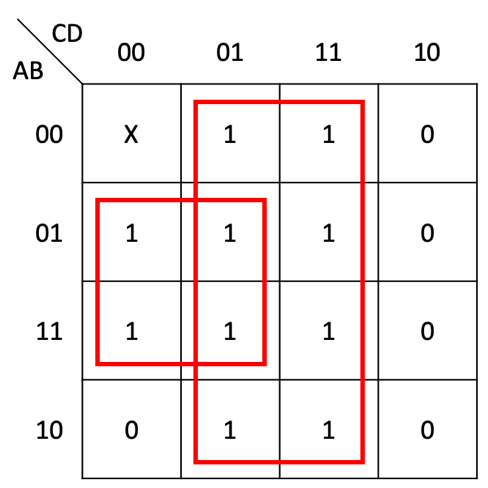
0x03 卡诺图的绘制

E0	E1

由于当且仅当? 均为 0 时 ?的值才设为 1，因此我们无需绘制卡诺图，就能构造出如下形式的逻辑表达式：

0x04 代码和仿真

💬 Design source：

`timescale 1ns / 1ps

module penc (
    input A,
    input B,
    input C,
    input D,
    output E0,
    output E1,
    output NR
);

assign E0 = C | D
assign E1 = B & (~C) | D
assign NR = (~A) & (~B) & (~C) & (~D)

endmodule

💬 Testbench：

`timescale 1ns / 1ps

module penc_tb;
reg A, B, C, D;
wire E0, E1, NR;

penc u_penc (
    .A(A),
    .B(B),
    .C(C),
    .D(D),
    .E0(E0),
    .E1(E1),
    .NR (NR )
);

initial begin
    A = 1'b0;
    B = 1'b0;
    C = 1'b0;
    D = 1'b0;
end

always@(A or B or C or D) begin
    A <= #10 ~A;
    B <= #20 ~B;
    C <= #40 ~C;
    D <= #80 ~D;
end

initial begin
    #160
    $finish;
end

endmodule

🚩 运行结果如下：

📜 Schematic：

所设计的优先级编码器按 D>C>B>A 的顺序具有高优先级。高优先级意味着例如当 ABCD 接收到输入值 0101 时，即使 B 和 D 的值都被设置为 1，它也会将 0101 的输入视为 0001，因为 D 的优先级高于 B。这样，一个输入位就可以作为编码器的输入，即使不是设置为 1 或 0 的单个位，也能返回输出值。

📌 [ 笔者 ]? ????
📃 [ 更新 ]? ?2022.9.20
? [ 勘误 ]?? /* 暂无 */
📜 [ 声明 ]? ?由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料? Introduction to Logic and Computer Design, Alan Marcovitz, McGrawHill, 2008 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/.