【索引的数据结构】第3章节:MySQL数据结构选择的合理性
目录结构

之前整篇文章太长,阅读体验不好,将其拆分为几个子篇章。
本篇章讲解 MySQL 数据结构选择的合理性。
MySQL 数据结构选择的合理性
B+Tree 中的根节点从创建开始是常驻内存中的,每次查询数据的时候,从内存中的根节点查找到合适的子节点记录(这一步是不需要磁盘 I/O 的),所有剩下最多三层节点,所以查询某一个键值的时候,最多只需要 1~3此磁盘 I/O。
全表扫描
全表扫描也就是使用的非主键列(且没有建立索引)作为 where 查询条件,只能进行全表扫描,性能非常差。
常见的加速查找速度的数据结构,常见的有两类:
- 树:例如平衡二叉树,增删改查的平均时间复杂度都是
O(log2N) - 哈希:利润 HashMap,增删改查的平均时间复杂度都是 O(1)
Hash 结构
Hash 本身是一个函数,也被称为散列函数,可以帮助我们大幅度提升检索数据的效率。
Hash 是通过某种特定的算法(MD5、Base64、SHA256 等)将输入转化为输出。
相同的输入永远可以得到相同的输出。
采用 Hash 进行检索效率非常高,基本上一次检索就可以找到数据,而 B+Tree 需要自顶向下一次查找,多次访问节点才能找到数据,中间需要多次 I/O 操作,从效率上来说 Hash 比 B+Tree 更快。
Java 中常用的 HashMap 和 HashSet 的底层就是用的哈希结构存储的数据。
在 Hash 的方式下,一个元素处于 h(k)中,即利用哈希函数算法,根据关键字 k 计算出一个哈希值(也就是在槽中的位置),函数 h 将关键字域映射到哈希表 T[0……m-1] 槽位上。
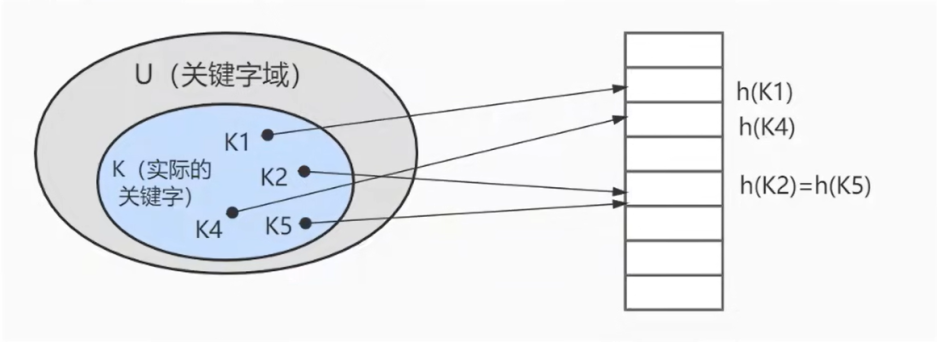
上图中哈希函数 h 有可能将两个不同的关键字映射到同一个位置,这叫作 哈希碰撞,在数据库中一般采用 链接法来解决,也就是将散列到同一个槽位上的元素放到一个链表中,如下图所示:
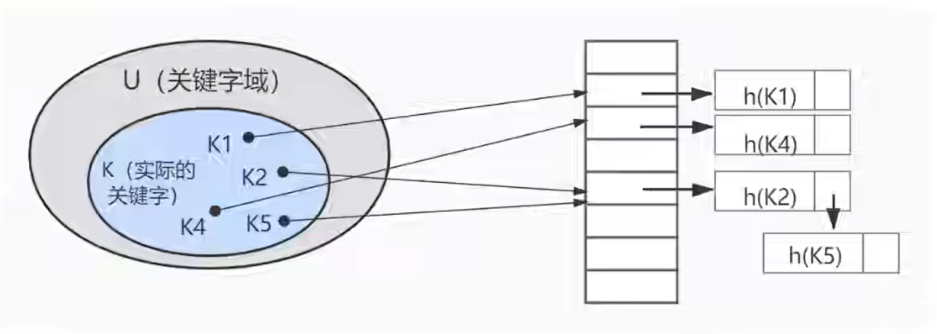
既然 Hash 结构效率高,那为什么 MySQL 索引结构要设计成树形结构呢?
- Hash 索引仅能满足(=)、(<>)、(IN)等条件查询,如果进行
范围查询,哈希型的索引时间复杂度会退化为 O(n);而树形的有序性依然可以保持 O(log2n) 的高效率。 - Hash 索引还有一个缺陷,数据的存储是
无序的,在 order by 的情况下,使用 Hash 索引还需要对数据重新排序 - 对于联合索引的情况,Hash 值是将联合索引键合并之后一起来计算的,无法对单独的一个索引键或者多个索引键进行查询
- 对于等值查询,通常 Hash 索引的效率很高。但是也有一种特殊的情况,就是
索引列的重复值有很多,效率就会很低下,这是因为遇到 Hash 冲突时,需要遍历桶中的行指针来进行比较,找到要查询的关键字,非常耗时,所以 Hash 索引一般不会用在重复值很多的列上,比如性别、年龄字段等。
Hash 索引适用存储引擎如下所示:

Hash 索引的适用性:
Hash 索引存在很多限制,相比之下 B+Tree 索引的适用会更加广泛,不过有些场景使用 Hash 索引会更加高效,比如在键值对数据库中,Redis 底层存储的核心就是 Hash 表。
另外,InnoDB 本身不支持 Hash 索引,但是提供了 自适应 Hash 索引(Adaptive Hash Index)。
什么情况下才会使用自适应索引呢?
如果某个数据经常被查询到,当满足一定条件时,就会将这个数据页的地址存储到 Hash 表中,这样下次查询的时候就可以直接到这个页面所在的位置,这样 B+Tree 也相当于具备了 Hash 索引的优点。

上图结构:
- 左边是自适应 Hash 索引之后的查询过程
- 右边是正常通过根节点查询叶子节点的过程
采用 Hash 索引目的是为了方便根据 SQL 的查询条件定位到叶子节点上,特别是 B+Tree 比较深的时候,通过自适应 Hash 索引可以明显提高数据的检索效率。
通过命令查看是否开启了自适应哈希索引:
show variables like '%adaptive_hash_index%'
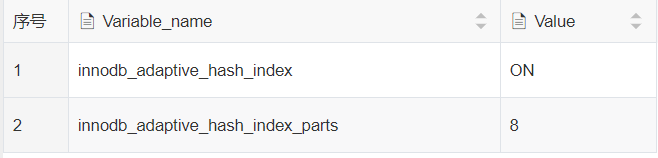
二叉搜索树
二叉搜索树的特点:
- 每个节点只能有两个子节点
- 左子节点 < 当前节点,右子节点 >= 当前节点
查询规则:
最基础的二叉搜索树,搜索某个节点和插入节点的规则一样,假设要搜索的的数值为 key:
- 如果 key 大于根节点,则在右子节点中进行查找
- 如果 key 小于根节点,则在左 子节点中进行查找
- 如果 key 等于根节点,那当前根节点就是要找的数据

特殊情况,如果给出的数据如下所示:

树结构偏了,这也不算很极端的情况,真实的数据很有可能这样存储,但是这样的二叉搜索树,在查询性能上就退化为了一条链表,时间复杂度也编程了 O(n),上面第一棵树的深度为 3(最多查询 3 次),第二棵树的深度是 7(最多查询 7 次),那如果树的深度更深,几十层、甚至成百上千层深,查询比对一次就是一次 I/O,那查询效率就会非常低下。
我们可以看出上面的树都有一个特点,就是 高瘦,每个节点最多只能有两个子节点,如果想提高查询效率,降低 I/O 次数,就要想办法减少树的深度,也就是要从 高瘦变为 矮胖。
AVL 树
为了解决上述二叉查找树退化为链表的问题,又提出了 平衡二叉搜索树,又被称为 AVL 树,它在二叉搜索树上增加了约束。
**特点:**它是一棵空树或左右两棵子数的高度差最大不会超过 1,并且两边的子树都是二叉平衡树。
如果树结构偏了,则让节点自动平衡旋正,如下图所示:

上面有 5 个层级,如果要查找的数据恰巧在第 5 层叶子节点中,需要经历 5 次 I/O 操作,虽然效率比上面的二叉平衡搜索树高了很多,但是如果数据量非常大,树的层级还是很多,I/O 次数依然会很多,效率也会很低。
这对这种情况,我们把 二叉树 改为了 M 叉树 (M>2),也就是说打破上面每个节点只有两个子节点的问题,如果 M=3,同样存储上述 31 个节点,结构如下:

每个节点都有 3 个子节点,整体变为了最多 4 次 I/O 操作。
这样看来,相比最开始的 高瘦,确实 矮胖了很多。
结论:M(M>2)叉树的高度远小于二叉树的高度。
B-Tree
B 树(Balance Tree),也称为 多路平衡查找树,简写为 B-Tree(中间的杠,是为了将其连起来,不是减号)。
它的高度远小于二叉平衡树。
B-Tree 的结构如下图所示:
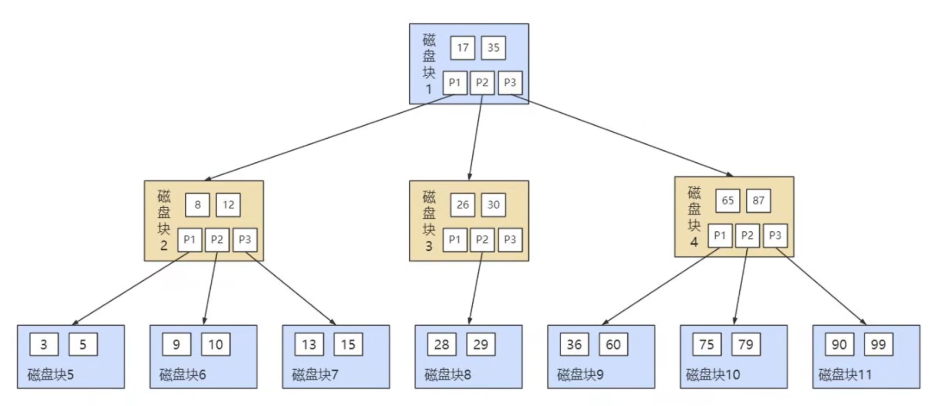
B-Tree 作为多路平衡二叉树,它的每一个节点最多可以包括 M 个子节点,M 称为 B 树的阶。
阶是每个磁盘最多容纳的关键字个数。
每个磁盘块中,包括了 关键字和 子节点的指针。
一个磁盘中包含 x 个关键字,那么指针数就是 x+1。
如果一个 B 树的阶是 100,树的层级为 3,那最多可以存储 100 万条数据。对于大量的索引数据,采用 B-Tree 的结构是非常合适的。
结论:
- B-Tree 相比于平衡二叉树来说磁盘 I/O 操作要少很多,查询效率也就越高。
- 只要树的高度足够低,I/O 次数足够少,查询效率就会越高。
- B-Tree 在增删改的时候会导致树不平衡,这个时候就需要树进行自旋保持树的自平衡。
- 关键字结合分布在整棵树中,也就是叶子节点和非叶子节点都会存储数据。
- 其搜索性能等价于在关键字集合内做一次二分查找。
真正 B-Tree 的结构如下:

B+Tree
B+Tree 也是一种多路搜索树,在 B-Tree 的基础上改进。
主流的 DBMS 都支持 B+Tree 的索引方式,相比于 B-Tree,B+Tree 更适合于文件索引系统。
B-Tree 和 B+Tree 的区别:
-
B-Tree 的每一个节点都存储数据, B+Tree 的中间节点不存储数据
-
B-Tree 查询不稳定,B+Tree 查询相对较稳定
-
B-Tree 查询效率较低,B+Tree 查询效率较高,以为捏 B+Tree
更矮胖(阶数更大,层数越少,I/O 次数越少) -
在查询范围上,B+Tree 的效率要更高
-
- B+Tree 的所有数据都在叶子节点上,并且数据是顺序排序的,可以通过指针查找
- B-Tree 的数据存储左右的节点上,需要通过中序遍历查找
B-Tree 和 B+Tree 都可以作为 MySQL 的所以结构,没有谁比谁更好,他们两个都有各自的应用场景,结合场景才能发挥各自的优势。
为了减少 I/O ,索引数会一次性加载到内存中吗?
索引都是存储在磁盘中的,如果数据量很大,那索引的大小也会很大,甚至几个 G。
所以不可能一次性加载到内存中,只能逐一加载每一个磁盘页,因为磁盘页对应着索引的节点。
B+Tree 的存储能力如何?为何说一般查找一个记录,最多只需要 1~3 次 I/O 操作?
首先我们清楚一个数据页的大小为 16KB,一般表的主键类型为 INT(4 个字节) 或 BIGINT(8 个字节),指针类型一般也为 4 个字节或 8 个字节,也就是一个数据页大概存储 【16KB / (8B+8B) = 1k 个键值】,因为这是非叶子节点不存储数据,所以键值会多一点,但真实的数据表一般都会挺大的,叶子节点中的每个页可能大概会存储 500-1000 条,假设我们取每页 500 条数据,一个深度为 3 的 B=Tree,可以维护 1000 _ 1000 _ 500 = 5 亿条数据。
实际上每个数据页可能存不满,因此在数据库中,B+Tree 的高度一般在 2~4层左右。假设达到了 4 层,那顶层也就是根节点,根据存储引擎的设计,根节点一般从创建开始数据页地址就会存储在内存中的某个地方,也就是说这个数据页不用磁盘 I/O 已经在内存中了,所以剩下三层,最多进行三次 I/O 操作,所有说查询一条记录,最多只需要 1~3 次 I/O 操作。
Hash 索引和 B+Tree 索引的区别?
- Hash 索引不能进行范围查询
- Hash 索引不支持联合索引的最左侧原则
- Hash 索引不支持 Order By 排序
- Hash 所用不支持模糊查询
- InnoDB 不支持 Hash 索引,但是支持自适应 Hash 索引(常用数据页的地址存储到 Hash 表中)
MySQL 支持的存储引擎对各类索引的支持?

R 树
R-Tree 在 MySQL 中很少使用,仅支持 geometry 数据类型,支持该类型的存储引擎如下:
- InnoDB、MyISAM、BDB、NDB、Archive 等

举例子:查询 20 英里以内所有的餐厅。正常情况下会将每个餐厅的(x,y)的经纬度分别存储到一个字段中,然后挨个去遍历查找,但是面对超大型地图数据库,这种遍历方式就不行了,效率非常低下,所以这个时候 R-Tree 的作用就出来了,很好的解决了解决了高纬度空间搜索问题。
R-Tree 是一棵用来 存储高纬度数据的平衡树。
小结
一句话,面对大数据量,索引不是万能的,没有索引是万万不能的。
本文内容总结借鉴于康师傅的 MySQL 视频课:https://www.bilibili.com/video/BV1iq4y1u7vj

一起学编程,让生活更随和!
如果你觉得是个同道中人,欢迎关注博主gzh:【随和的皮蛋桑】。
专注于Java基础、进阶、面试以及计算机基础知识分享🐳。偶尔认知思考、日常水文🐌。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!