理解VAE（变分自编码器）

1.贝叶斯公式

贝叶斯理论的思路是，在主观判断的基础上，先估计一个值（先验概率），然后根据观察的新信息不断修正(可能性函数)。

P(A)：没有数据B的支持下，A发生的概率，也叫做先验概率。这完全是根据经验做出的判断，这也是前面说的贝叶斯公式的主观因素部分。

P(A|B)：在数据B的支持下，A发生的概率，也叫后验概率。即在B事件发生之后，我们对A事件概率的重新评估。

P(B|A)：给定某参数A的概率分布：也叫似然函数。这是一个调整因子，即新信息B带来的调整，作用是使得先验概率更接近真实概率。至于新信息带来的调整作用大不大，还得看因子的值大不大。

假如我在大学校园中随机找出一个人B，身高170，体重60。P(A)是大学中男生的占比，是先验概率。

那么从所有男生中选出身高170，体重60的人的概率就是似然概率，也就是从男生的分布（男生的概率密度函数）中得到B的概率。

那么选出的这个人B是男生的可能性就是后验概率P(A|B)。

无监督学习中的一个核心问题就是——密度估计问题。要训练出一个模型，使该模型的概率密度函数和真实的训练数据分布尽可能相似。

2.生成模型分类

无监督学习两种典型思路：

1.显式密度估计：显式的定义并求解分布Pmodel(x)。分布的方程是能够写出来定义出来的。可以算出特征空间中选取的点生成的样本可信度，概率值。

2.隐式的密度估计：学习一个模型Pmodel(x)，无需显式的公式定义。只能够生成样本。只会产生特征空间中概率比较大，与真图相似的点。

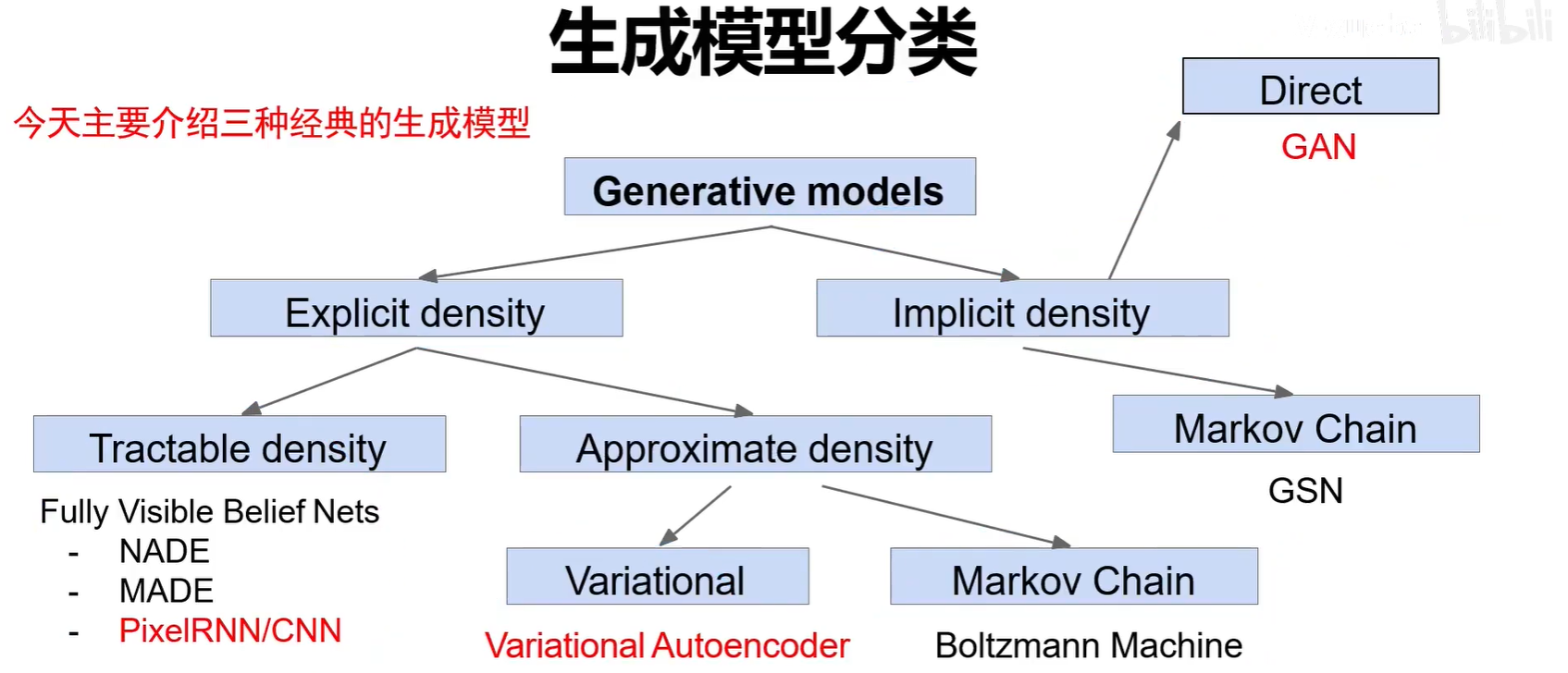
生成模型主要分为显示概率密度-可求解，显式概率密度-可近似和隐式概率密度。

2.1 PixelRNN与PixelCNN

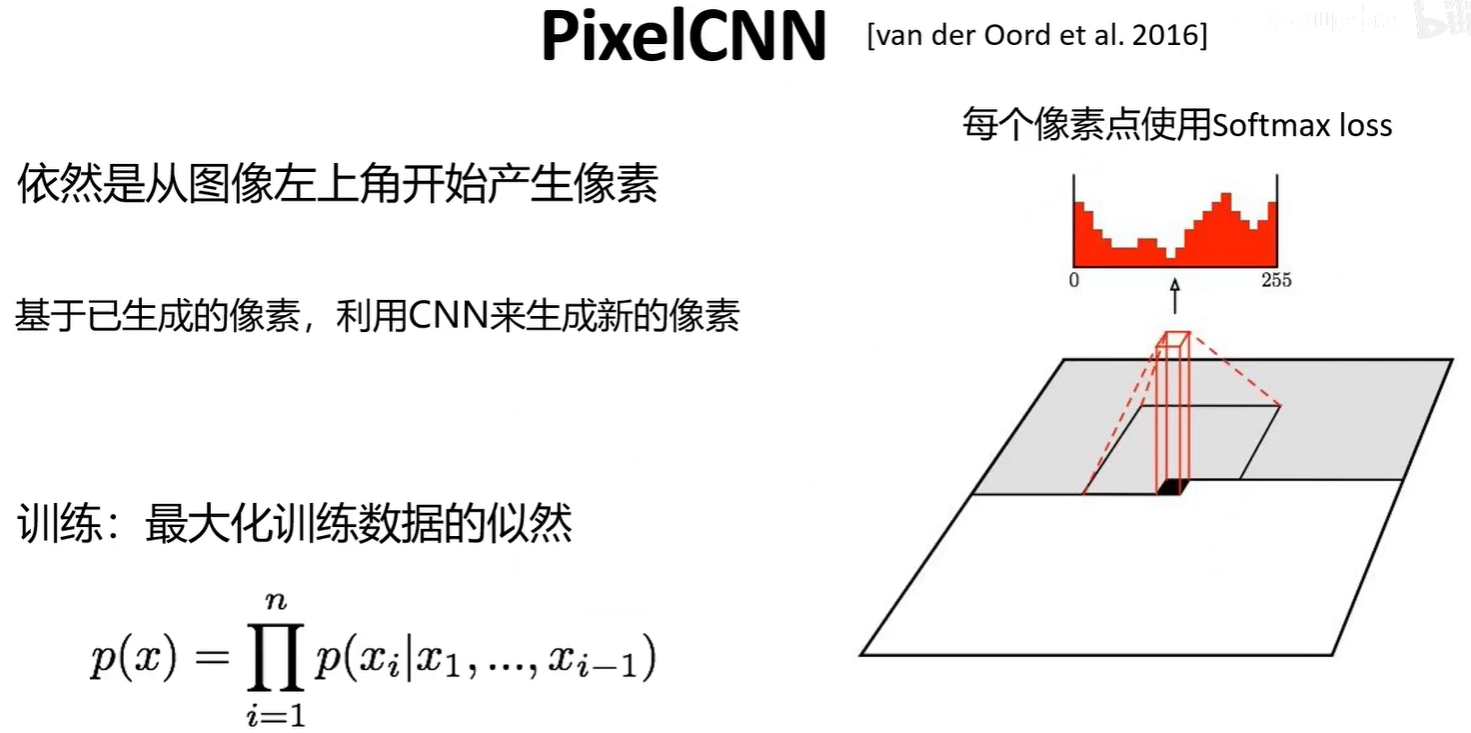
PixelRNN与PixelCNN是前面的像素生成后，来预测下一个像素的值，在知道前面的像素值后，该像素值的概率分布（0-255的每个值的概率）是可以计算出来的。

2.2 VAE

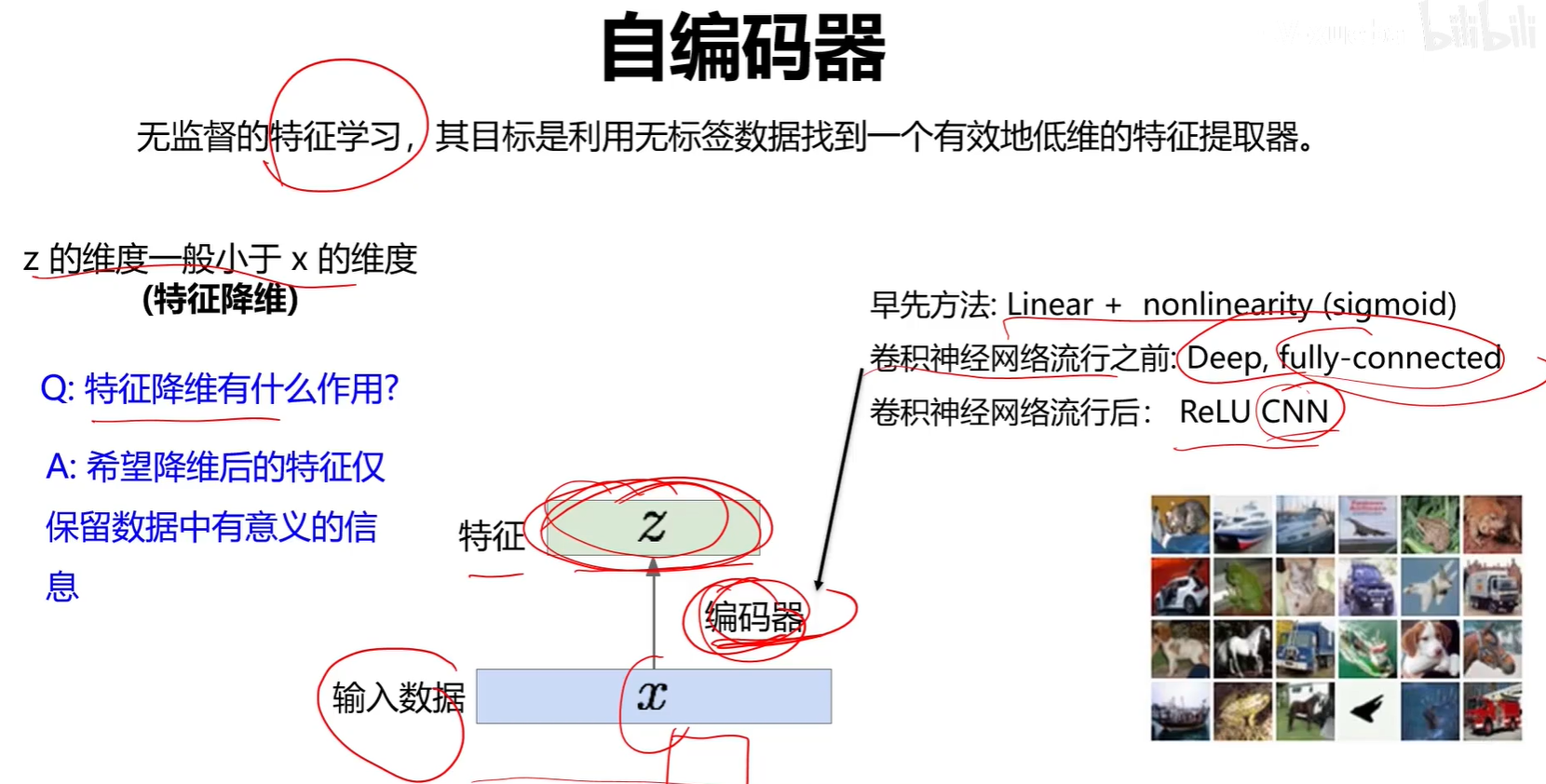
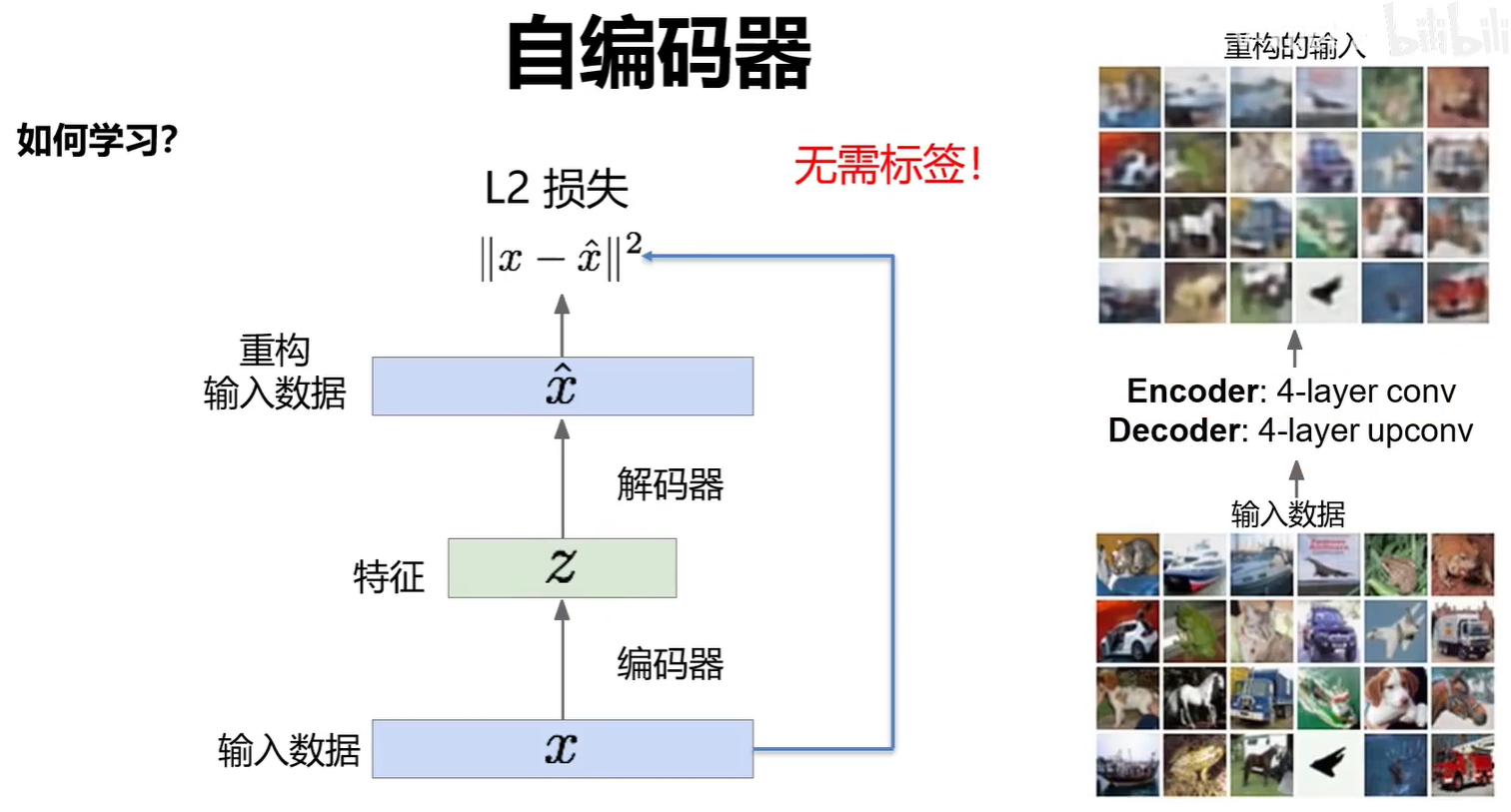
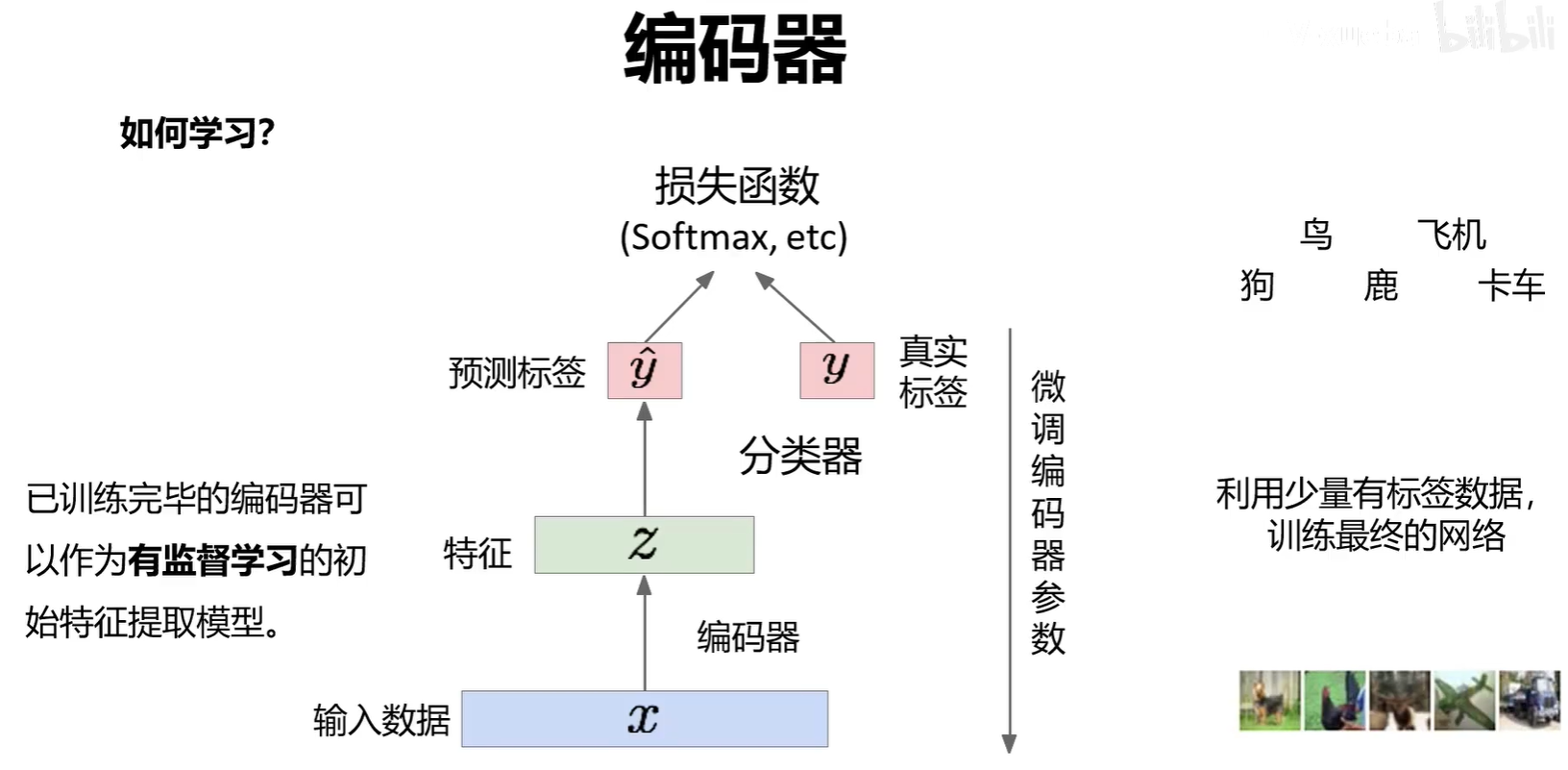
编码器可以单独作为一个特征提取网络来进行分类任务。

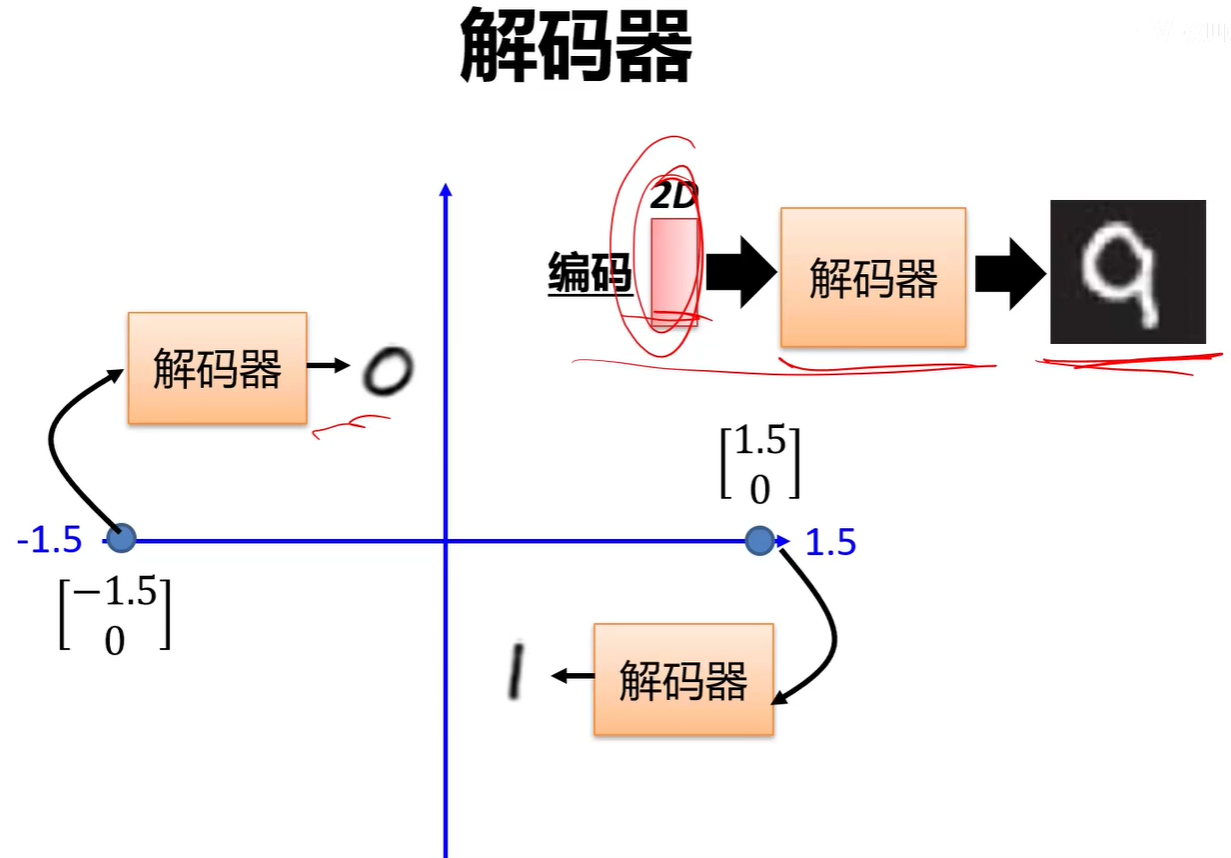
解码器可以单独分割出来作为一个图像生成器。

2.2.1 香农熵、交叉熵、KL散度

信息量：一个不太可能发生的事件居然发生了，我们收到的信息要多于一个非常可能发生的事件发生。

用一个例子来理解一下，假设我们收到了以下两条消息：

A：今天早上太阳升起

B：今天早上有日食

我们认为消息A的信息量是如此之少，甚至于没有必要发送，而消息B的信息量就很丰富。利用这个例子，我们来细化一下信息量的基本想法：①非常可能发生的事件信息量要比较少，在极端情况下，确保能够发生的事件应该没有信息量；②不太可能发生的事件要具有更高的信息量。事件包含的信息量应与其发生的概率负相关。

事件x的信息量为：

该信息量公式只能处理随机变量的取指定值时的信息量。要对整个概率分布的平均信息量进行描述时用香农熵。

香农熵：具体方法为求上述信息量函数关于概率分布的期望，这个期望值（即熵）为：

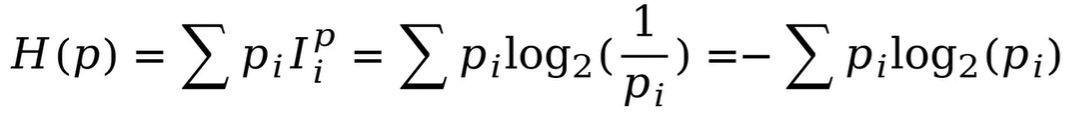
当概率分布连续时，求和号变积分号。

那些接近确定性的分布（输出几乎可以确定）具有较低的熵，那些接近均匀分布的概率分布具有较高的熵。比如硬币两面的概率都是0.5，那么他的熵就高。如果硬币两面概率分别是0.2和0.8，那么他的熵就低。

KL散度：假设随机变量的真实概率分布为P(X)，而我们在处理实际问题时使用了一个近似的分布Q(X)来进行建模。由于我们使用的是Q(X)而不是真实的P(X)，所以我们在具体化的取值时需要一些附加的信息来抵消分布不同造成的影响。我们需要的平均附加信息量可以使用相对熵，或者叫KL散度（Kullback-Leibler Divergence）来计算，KL散度可以用来衡量两个分布的差异：

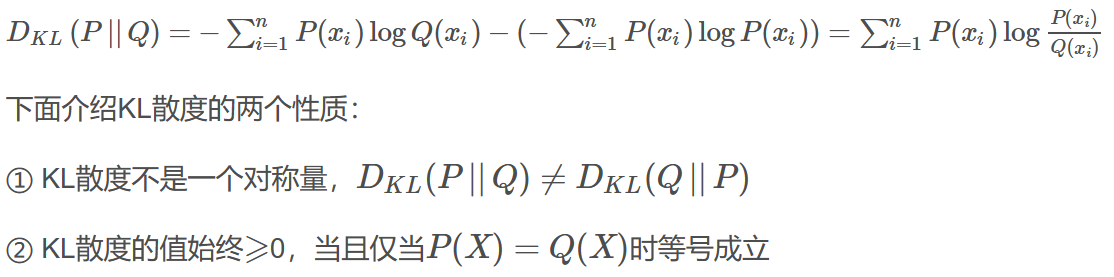
交叉熵：交叉熵与上面介绍的KL散度关系很密切，让我们把上面的KL散度公式换一种写法：

交叉熵H(P,Q)就等于：?

如果把P看作随机变量的真实分布的话，KL散度左半部分的?H(P(X))其实是一个固定值，KL散度的大小变化其实是由右半部分交叉熵来决定的，因为右半部分含有近似分布Q，我们可以把它看作网络或模型的实时输出，把KL散度或者交叉熵看做真实标签与网络预测结果的差异，所以神经网络的目的就是通过训练使近似分布Q逼近真实分布P。从理论上讲，优化KL散度与优化交叉熵的效果应该是一样的。所以我认为，在深度学习中选择优化交叉熵而非KL散度的原因可能是为了减少一些计算量，交叉熵毕竟比KL散度少一项。

2.2.2 变分推理

隐变量图模型：隐变量一般表示了一些被观测变量（也就是输入样本）的属性，这样隐变量和被观测变量就组成了隐变量图模型。

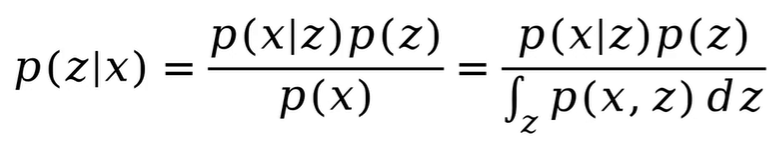
由于分母的联合概率密度函数不好求，也就是边缘概率P(x)不好求，所以导致整个后验概率P(z|x)不好求。

推理：一般我们会观测数据来获得对数据的见解或知识，这就是从被观测变量数据推理无法直接观测的隐变量的过程。

变分：既然真实的后验概率分布比较复杂，那么我们尝试使用一组比较简单并且可以参数化的概率分布去近似它。近似的过程就是变分。

变分推理：使用近似的概率分布去完成在给定被观测变量的情况下对隐变量概率分布估计的过程就叫做变分推理。

2.2.3 ELBO

我们想要使得近似分布q尽可能等于后验概率p(z|x)，就要使他们之间的KL散度最小。因为logp(x)与隐变量z无关，所以可以移到期望外面，KL散度简化完的公式为

将logp(x)移到左边后为

由于p(x)是被观测变量，在隐空间是一个定值。KL散度又是大于等于0，且分布相同时才等于零。所以要想最小化q和p(z|x)的KL散度，就需要最大化期望 E[logp(z,x)-logq(z)]，也就是最大化证据下界ELBO：

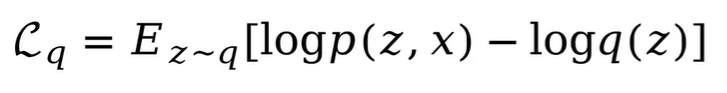
我们可以自己选一个符合一般概率分布的近似分布q，通过最大化ELBO（求导求极值）来使得q的曲线逼近真实后验概率分布曲线。

2.2.4 变分自编码器

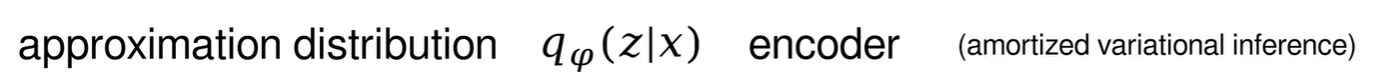
VAE中的编码器就是后验概率p(z|x)，可以通过q(z)来近似，q(z)也可以写作q(z|x)。

VAE中的解码器就是似然函数p(x|z)。

ELBO就可以改写为：

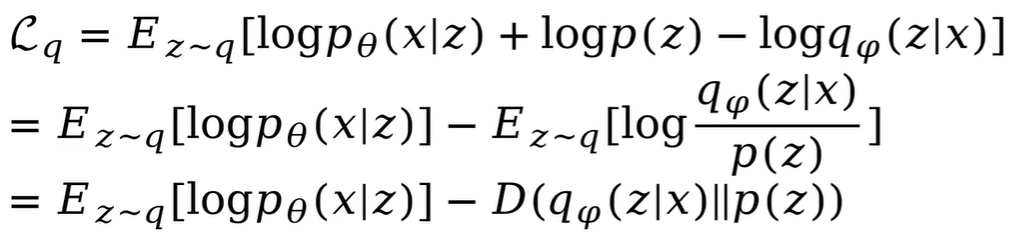
最大化ELBO就需要最大化第一项最小化第二项。

第一项是似然函数在近似分布q下的期望，表示重建的相似度，p(x|z)是一个高斯分布，z是编码器生成的均值，x是输入的样本，高斯分布中均值是概率密度最高的地方，所以最大化第一项相当于使神经网络预测的均值越靠近输入样本。

第二项是近似分布q，也就是编码器，与隐变量先验分布p(z)的KL散度，为了方便计算，我们给定p(z)为单位高斯分布，均值为0，方差是单位矩阵。这里最小化KL散度就是使编码器输出的隐变量分布和单位高斯分布更加接近。

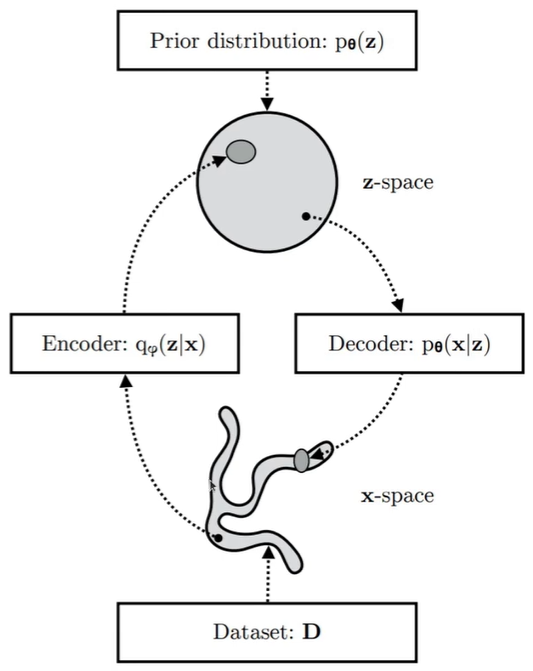
上图是VAE的简要示意图，复杂分布的输入数据通过编码器映射到隐空间中，使得隐变量的概率密度靠近先验分布，也就是单位高斯分布。解码器将简单分布的隐变量通过解码器映射到复杂分布的图像概率空间中。

2.2.5 目标函数

首先是编码器部分的目标函数：?

首先看一下KL散度这一项，q是符合高斯分布的，均值和方差是由神经网络生成的。p（z）符合单位高斯分布。其中是参数化的神经网络。

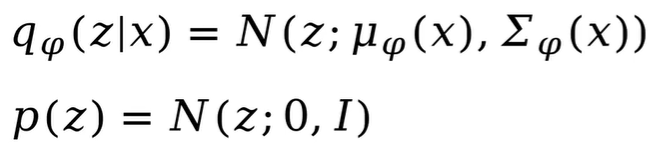
两个高斯分布之间的KL散度是有解析解的。代入q和p(z)的高斯分布，化简如下。

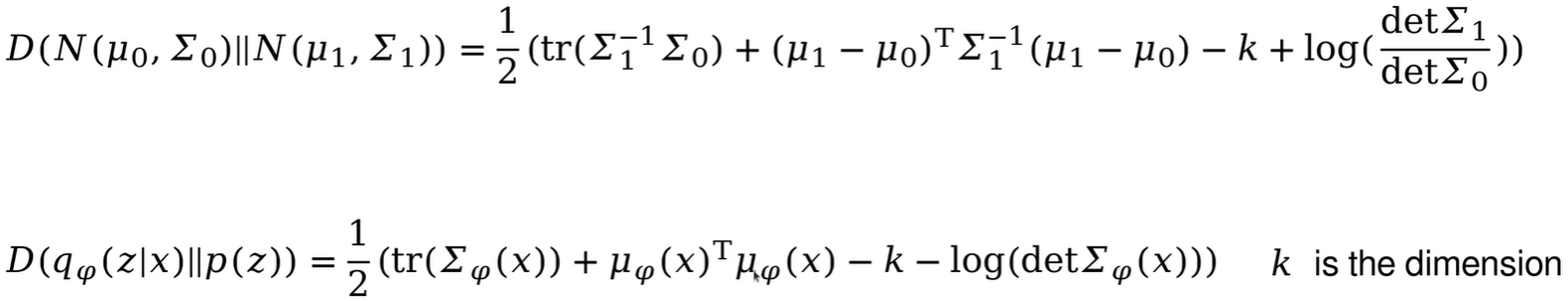
然后是解码器部分的目标函数：

其中，p(x|z)是一个高斯分布，是参数化的神经网络，神经网络输出该高斯分布的均值。p（x|z）的log值化简如下，x是样本标签，也就是原图，是神经网络输出值，最后就是求他两的二范数。

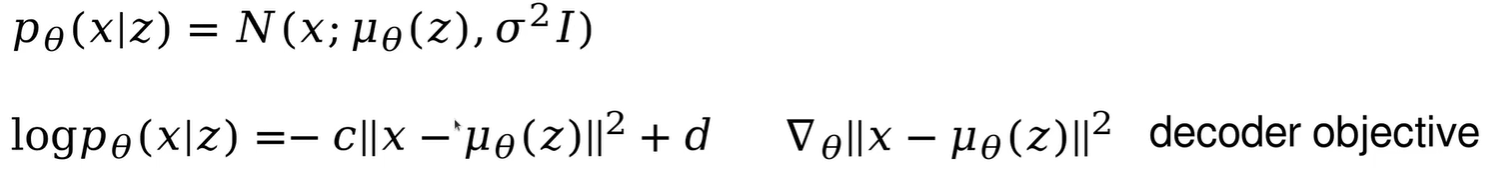
但是该目标函数取决于隐变量z，z是从近似分布q中采样得到的，所以在对求梯度反向传播时就不行。

2.2.6 重参数化

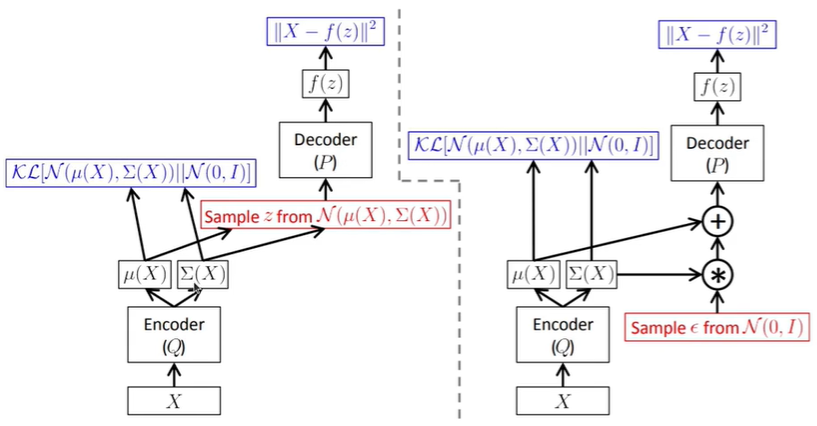
上图是VAE的整个流程图，输入数据x通过编码器得到近似分布q的均值和方差，然后与单位高斯分布p(z)计算KL散度。

然后对近似分布q进行采样得到隐变量z，将z送入解码器中得到重建的预测值，然后将预测值与原图计算二范数。但是由于采样是随机的，不能反向传播，所以我们需要重参数化。

重参数化就是，任意高斯分布都可以写成均值+标准差*单位高斯分布的形式。所以任意高斯分布的采样都可以写成均值+标准差*单位高斯分布采样的形式。反向传播时，标准高斯分布的采样可以当作常数。