排序之归并排序
????????归并排序是第一个可以被实际使用的排序算法。归并排序性能不错,其复杂度为O(nlogn)。
????????归并排序是一种分治算法。其思想是将原始数组切分成较小的数组,直到每个小数组只有一
个位置,接着将小数组归并成较大的数组,直到最后只有一个排序完毕的大数组。
var mergeSort = function(array) {
array = mergeSortRec(array)
}
var mergeSortRec = function(array){
var length = array.length
if(length ===1 ) // {1}
return array // {2}
var mid = Math.floor(length/2), // {3}
left = array.slice(0,mid), // {4}
right = array.slice(mid,length) // {5}
return merge(mergeSortRec(left),mergeSortRec(right)) // {6}
}
var merge = function(left,right){
var result = [], // {7}
il=0,
ir=0
while(il<left.length && ir<right.length){ // {8}
if(left[il]<right[ir]){
result.push(left[il++]) //{9}
}else{
result.push(right[ir++]) // {10}
}
}
while (il < left.length){ // {11}
result.push(left[il++]);
}
while (ir < right.length){ // {12}
result.push(right[ir++]);
}
return result // {13}
}????????归并排序将一个大数组转化为多个小数组直到只有一个项。由于算法是递归的,我们需要一
个停止条件,在这里此条件是判断数组的长度是否为1(行{1})。如果是,则直接返回这个长度
为1的数组(行{2}),因为它已排序了。
????????如果数组长度比1大,那么我们得将其分成小数组。为此,首先得找到数组的中间位(行{3}),找到后我们将数组分成两个小数组,分别叫作left(行{4})和right(行{5})。left数组由
索引0至中间索引的元素组成,而right数组由中间索引至原始数组最后一个位置的元素组成。
????????merge函数(行{6}),它负责合并和排序小数组来产生大数组,直到回到原始数组并已排序完成。为了不断将原始数组分成小数组,我们得再次对left数组和right数组递归调mergeSortRec,并同时作为参数传递给merge函数。
????????merge函数接受两个数组作为参数,并将它们归并至一个大数组。排序发生在归并过程中。
首先,需要声明归并过程要创建的新数组以及用来迭代两个数组(left和right数组)所需的两
个变量(行{7})。迭代两个数组的过程中(行{8}),我们比较来自left数组的项是否比来自right
数组的项小。如果是,将该项从left数组添加至归并结果数组,并递增迭代数组的控制变量(行
{9});否则,从right数组添加项并递增相应的迭代数组的控制变量(行{10})。
????????接下来,将left数组或者right数组所有剩余的项添加到归并数组中(行{11}和行{12})。最后,将归并数组作为结果返回(行{13})。
????????如果执行mergeSort函数,下图是具体的执行过程:
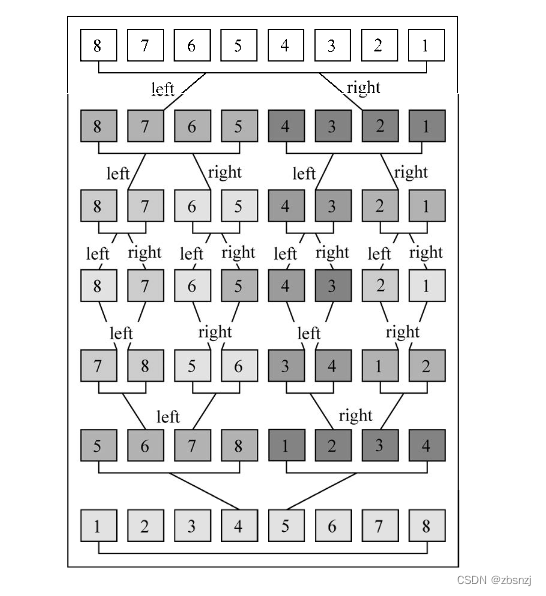
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!