LeetCode 1901. 寻找峰值 II:二分查找
2023-12-20 09:20:49
【LetMeFly】1901.寻找峰值 II:二分查找
力扣题目链接:https://leetcode.cn/problems/find-a-peak-element-ii/
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
?
?
示例 1:
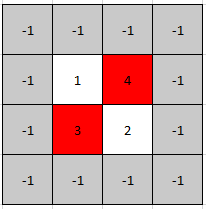
输入: mat = [[1,4],[3,2]] 输出: [0,1] 解释:?3 和 4 都是峰值,所以[1,0]和[0,1]都是可接受的答案。
示例 2:
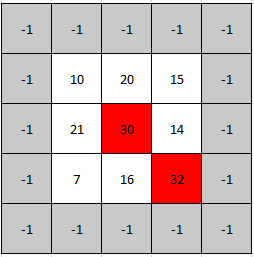
输入: mat = [[10,20,15],[21,30,14],[7,16,32]] 输出: [1,1] 解释:?30 和 32 都是峰值,所以[1,1]和[2,2]都是可接受的答案。
?
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105- 任意两个相邻元素均不相等.
方法一:一路爬山
从任意一点出发不断“爬山”:若这一点四周都比这一点低则返回这一点的坐标;否则从这一点移动到比这一点更高的相邻点。
- 时间复杂度 O ( n m ) O(nm) O(nm),其中 m a t mat mat未 n n n行 m m m列
- 空间复杂度 O ( 1 ) O(1) O(1)
小数据下方法二不一定快于方法一,但其不失为一个不错的思路。阅读前可参考上一题162.寻找峰值。
方法二:二分查找
二分查找有点类似于方法一的“跳跃式爬山”版本。从第一行到最后一行按行进行二分。二分到第mid行时:
- 找到mid行的最大值所在位置(mid, maxLocation)。
- 若此点比其上下两点都大,则直接返回此点坐标
- 若此点上方的点比其大,则说明“爬山路线”以及“山顶”都在mid这一行的上方(这个点是这一行最大的了,爬山路线不可能穿过mid行),开始二分[0, mid - 1]
- (否则)若此点下方的点比其大,开始二分[mid + 1, 行数 - 1]
以上。
- 时间复杂度 O ( m log ? n ) O(m\log n) O(mlogn),其中 m a t mat mat未 n n n行 m m m列
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
public:
vector<int> findPeakGrid(vector<vector<int>>& mat) {
int l = 0, r = mat.size();
while (l < r) {
int mid = (l + r) >> 1;
int maxLocation = max_element(mat[mid].begin(), mat[mid].end()) - mat[mid].begin();
if (mid - 1 >= 0 && mat[mid - 1][maxLocation] > mat[mid][maxLocation]) {
r = mid;
}
else if (mid + 1 < mat.size() && mat[mid + 1][maxLocation] > mat[mid][maxLocation]) {
l = mid + 1;
}
else {
return {mid, maxLocation};
}
}
return {}; // Fake Return
}
};
Python
# from typing import List
class Solution:
def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
l, r = 0, len(mat)
while l < r:
mid = (l + r) >> 1
maxLocation = mat[mid].index(max(mat[mid]))
if mid - 1 >= 0 and mat[mid - 1][maxLocation] > mat[mid][maxLocation]:
r = mid
elif mid + 1 < len(mat) and mat[mid + 1][maxLocation] > mat[mid][maxLocation]:
l = mid + 1
else:
return [mid, maxLocation]
return [] # Fake Return
同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/135083347
文章来源:https://blog.csdn.net/Tisfy/article/details/135083347
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!