详解“量子极限下运行的光学神经网络”——相干伊辛机

量子计算和量子启发计算可能成为解答复杂优化问题的新前沿,而经典计算机在历史上是无法解决这些问题的。
当今最快的计算机可能需要数千年才能完成高度复杂的计算,包括涉及许多变量的组合优化问题;研究人员正在努力将解决这些问题所需的时间缩短到几秒钟。
纵观全球科研团队,中国、日本(例如NTT研究所、东京工业大学和东京大学等)、美国(加州理工学院、哈佛大学、麻省理工学院、圣母大学、斯坦福大学、康奈尔大学、密歇根大学等)各界团队一直在探索利用量子和经典计算混合原理的尖端计算系统,也有研究团队认为相干伊辛机(CIM)是迄今为止最有前途的下一代解决方案。
离散变量和连续变量的优化问题(其中一些属于复杂性理论中的NP-hard或NP-complete类)在许多重要领域无处不在,包括操作和调度、药物发现、无线通信、金融、集成电路设计、压缩传感和机器学习等。
尽管算法和数字计算机技术都在飞速发展,但即使是实际中出现的中等规模的NP-hard或NP-complete问题,在现代数字计算机上也很难解决。
另一种备受当代人关注的方法是绝热量子计算(AQC)和量子退火(QA),当下,复杂的AQC/QA设备已在开发之中,但在量子比特之间提供密集连接仍是一大挑战,对AQC/QA系统的效率有严重影响。
简并光学参量振荡器(degenerate optical parametric oscillators,DOPO)网络是一种可供选择的物理系统,它具有非常规的运行机制,可用于解决伊辛问题以及许多其他组合优化问题。
相干伊辛机(CIM)是一个光学参量振荡器 (OPO) 网络,通过编程来解决映射到伊辛模型的问题。伊辛模型是磁性系统的数学抽象,由相互竞争的基本粒子自旋或角动量组成。
这其中,OPO是一种相干光源,与激光器类似,基于光学谐振器内的参量放大。有了伊辛模型,优化问题就可以映射到OPO上,OPO就可以找到最低能量的自旋配置,从而找到问题的解决方案。
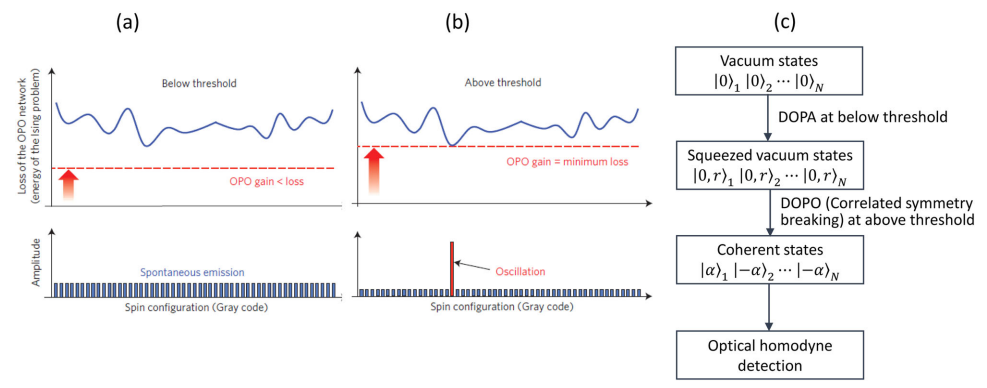
相干伊辛机(CIM)的原理和操作顺序。a, b)相干伊辛机(CIM)的原理。当DOPO网络增益增加到接地态的最小损耗率时,接地态会发生单模振荡

与传统计算机相比,CIM有两个明显的优势:速度和能效。
CIM中使用的光学和激光使其在带宽方面具有很大的优势:约200THz ,而传统计算机的带宽仅为几千兆赫,从而加快了通信和计算速度。与电路相比,光路还可以同时进行计算,同时最大限度地降低能耗。
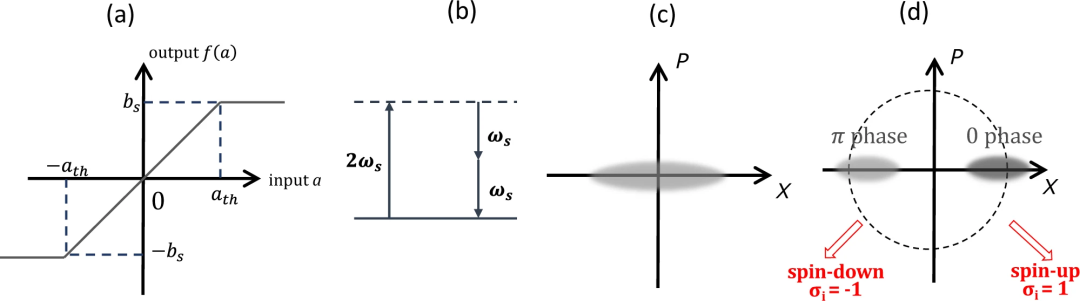
量子神经元的基本特性。a)经典神经网络中神经元的非线性输入输出关系;b)退化光学参数过程。低于阈值时 DOPA 的量子噪声分布(c)和高于阈值时DOPO的量子噪声分布(d)
具有上图(a)所示特征输入输出关系的非线性器件代表了经典神经网络(CNN)中神经元的典型增益函数。当输入信号电平较弱时,神经元会线性放大该输入信号,从而补偿网络中不可避免的线性损耗。然而,当输入信号电平超过某个阈值时,输出信号电平就会被箝制在一个恒定值上。
这种非线性的输入输出关系对于CNN找到一个稳定的工作点至关重要,而这个稳定的工作点就体现了给定数学问题的解决方案。在这一模型中,每个神经元的状态都由一个连续变量表示,它服从由以下因素控制的连续时间演化:
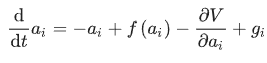
式中的第一项表示线性损耗,第二项表示自反馈,其非线性增益函数f如本节图(a)所示。需要注意的是,时间是由神经元激励的衰减率归一化的。
第三项表示神经元之间的相互耦合,相互作用势V实现了给定的数学问题。要强调的是,由于第三项的梯度下降特性,神经元之间可以同时相互耦合,而不会带来不必要的不稳定性或振荡。
非线性增益函数f通常用作第三项相互耦合的耦合系数,而不是第二项自反馈。最后,第四项gi表示与神经元激励衰减和非线性增益相关的噪声驱动力。
即使神经网络受到内部和/或外部噪声的随机驱动,每个神经元在给定时间仍具有不可预测但确定的值ai。当热噪声远大于量子零点噪声(即kBT)时,这是神经网络的正确物理图景。
量子神经元(或量子神经网络)具有以下三个特性,因此它有别于经典神经元:
1)量子神经元处于不同神经激励的叠加态,因此可以实现量子并行搜索(quantum parallel search);
2)量子神经元网络在相变临界点通过相关和集体对称性破缺做出决定,以达到最终的计算结果;
3)量子神经元网络通过玻色终态刺激将上述量子解放大为经典信号。
与经典神经网络相比,基于DOPO的量子神经网络最重要的优势在于,每个神经元(DOPO)都是在不同同相振幅特征态(即挤压真空态)的线性叠加中制备的,因此可以在整个优化过程中实现量子并行搜索。
——这是CIM至关重要的计算资源。

1)简并光学参量放大器和振荡器
我们在此重点讨论双光子发射过程的简并光学参量放大器(DOPA)。
一种特殊的设备由一个置于光腔中的二阶非线性晶体组成。非线性晶体吸收一个频率为2ωs的泵浦光子,同时发射两个频率为ωs的信号光子。相关的相互作用哈密顿量表示为:
![]()
由于量子干涉,如果一个DOPA由外部真空状态(零点波动)输入,零点波动会分别沿X轴和P轴放大和缩小。由此产生的状态被称为挤压真空态,它是最小不确定性波包,满足海森堡不确定性原理的相等原则,与真空态一样。
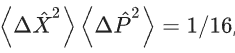
上述相位敏感放大/去放大现象在自然界中并不罕见。一个经典的例子是由人驱动的摆动,如图所示,人(相当于DOPA中的泵)完成了一个完整的周期(上-下-上),而摆动(相当于DOPA中的信号)只完成了半个周期(从左到右)。
请注意,如图(b)所示,泵和信号的相位应相互锁定,以实现振幅放大过程。这相当于同相振幅X ?被放大的情况。在童年的记忆中,你可以很容易地想象出,当你必须回家时,为了停止荡秋千,你会怎么做。你站在秋千中心,蹲在秋千两端。这样,秋千(信号)的振幅就会减弱。这相当于正交相位振幅P ?被去放大。
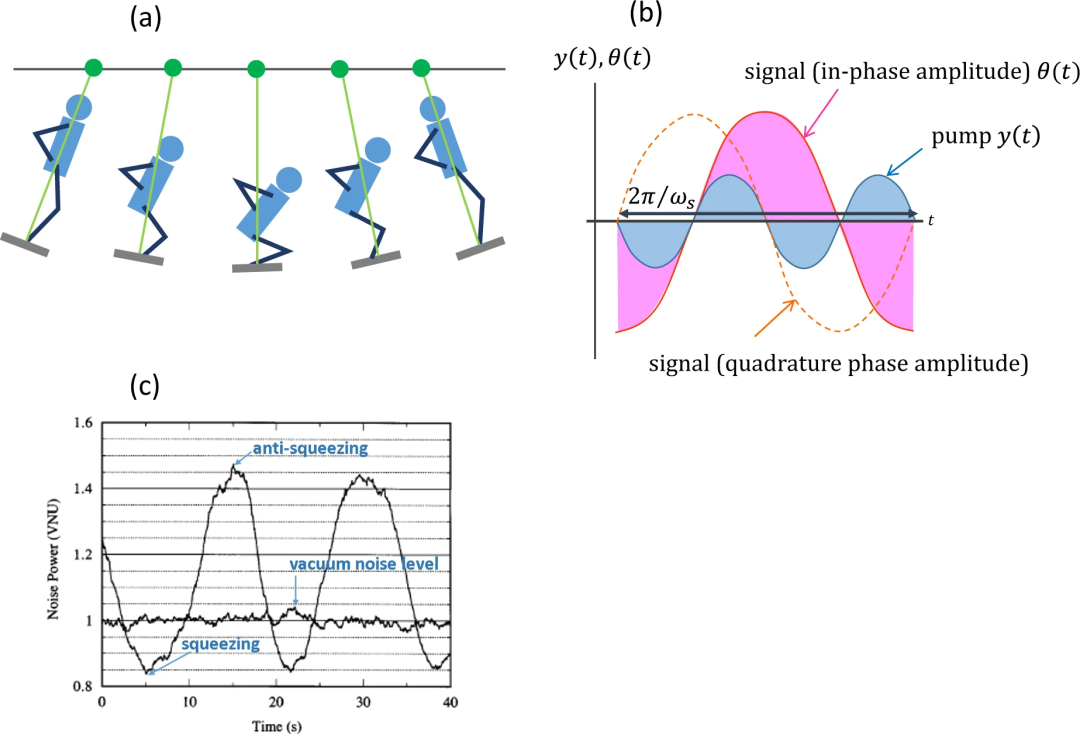
a)摆动的相位敏感放大/去放大过程,其中人做一个完整的周期(上-下-上),但摆动只做半个周期(从左到右)。b)人的驱动力y(t)和摆动振荡θ(t)之间的相应相位关系
在相干伊辛机(CIM)中,周期性极化铌酸锂(PPLN)波导器件被用作信号脉冲的PSA。“挤压”装置的一个普遍特性是,挤压(真空噪声去放大)程度会因实验系统的缺陷,特别是线性光学损耗而降低,但反挤压(真空噪声放大)程度却不会因线性光学损耗而降低。假设PSA输出有20 dB的挤压:
![]()
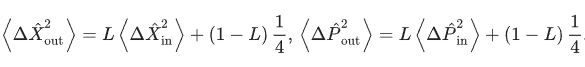
如果在PSA之后有3dB的线性损耗,则挤压程度仅为~3dB,而反挤压程度仍为~17dB。伊辛自旋是用同相振幅而不是正交相位振幅来表示的;因此,CIM中的量子并行搜索是基于同相振幅的反挤压量子噪声,而不是正交相振幅的挤压量子噪声,从而使CIM的运行在光损耗时具有固有的鲁棒性。
当信号功率增加到饱和水平以上时,DOPA的输入输出关系近似再现了非线性响应函数。这种增益饱和背后的物理机制是泵浦功率耗尽,从而引发反向能量流,即两个信号光子同时被非线性晶体吸收,产生一个泵浦光子。当输入信号功率变得足够大时,从信号到泵浦的反向能量流被开启,线性放大过程必须停止。
如果参量放大器的增益超过了空腔的信号衰减率,系统就能通过沿X方向产生有限的平均振幅来维持稳态场。
那么,为什么DOPO被称为量子神经元,它们与经典神经元有何不同?
2)线性叠加
光子数特征状态集|n?可以将场的任意状态扩展为一个正交集。挤压真空态的波函数可以用数学方法构建为具有偶数特征值的光子数特征态的叠加:
![]()
上述公式背后的简单物理推理解释如下:强泵浦场的光子数具有很大的量子不确定性,因此,即使在原则上,我们也无法提取非线性晶体中吸收的泵浦光子数在给定时间内是零、一个、两个......的路径信息;因为一个泵浦光子会转换成两个信号光子。
由于缺乏路径信息,DOPA输出信号场量子态的正确表达式必须是这些状态的叠加。
不难看出,不同的同相振幅特征态在以P为中心的小P区域内相互建设性地干扰,而在以P为中心的大P区域内相互破坏性地干扰。因此,沿X轴更多的反挤压(量子噪声增强)会实现沿P轴更多的挤压(量子噪声减弱)。
由DOPA产生的挤压真空态允许以有限能量进行量子平行搜索,而经典混合态则不允许这种量子平行搜索。
DOPA/DOPO的一个特别独特的量子特性是,如果“空穴损耗”(cavity loss)较小,上述叠加不仅能在阈值以下存活,而且在一定程度上也能在阈值以上存活。
在远高于振荡阈值时,DOPO会产生0相或π相相干场。之所以能做到这一点,是因为对泄漏信号场进行假设测量时,由于沿X轴的量子噪声增强以及两种状态之间的间隔较小,无法确定DOPO选择的是哪种相位。反挤压同相振幅噪声为这种假设的路径测量实现了所谓的“量子擦除”(quantum erasure)。
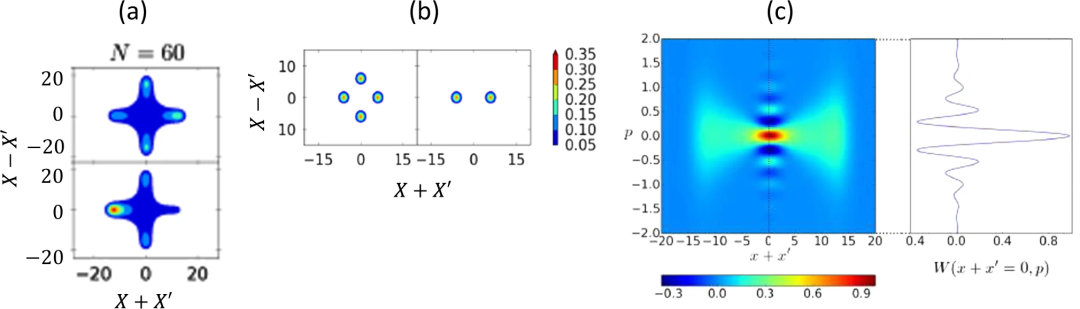
DOPO场在阈值时的量子态
3)相位敏感放大器提供的振幅和相位误差校正能力
外部注入的相位和振幅噪声会在DOPO场中引起波动。DOPO场的振幅和相位都是连续变量,因此无法采用标准的误差检测和误差修正技术。
幸运的是,只要相位误差小于±π/2,DOPO的相位敏感放大/去放大机制就能将相位稳定在0或π。如果信号振幅增大到稳态值以上,泵浦振幅的消耗就会更大,这反过来又会通过减小参数增益来恢复稳态振幅。
当信号振幅降低到稳态值以下时,情况则相反。光线性损耗导致的确定性振幅衰减可以通过平均增益来补偿。这样,输出振幅就通过DOPO的线性空腔损耗和饱和增益之间的平衡得到稳定,而相位则通过DOPO的相位敏感去放大作用得到稳定。
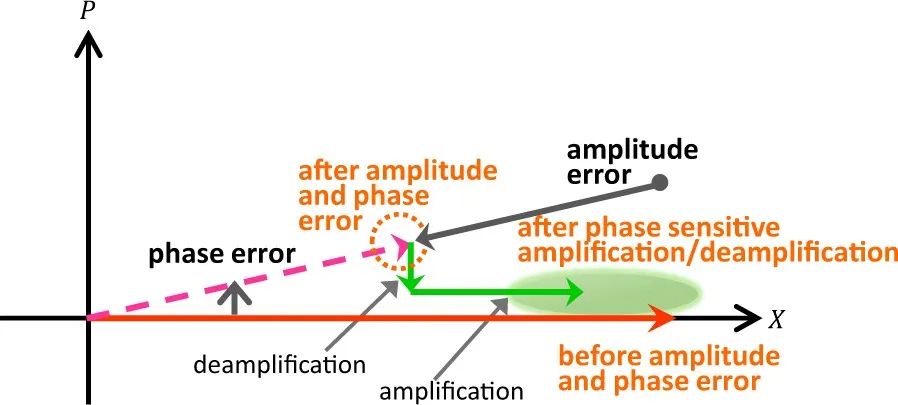
DOPO的振幅和相位误差校正。振幅误差通过沿X轴的饱和放大进行校正,相位误差通过沿P轴的相位敏感去放大进行校正
DOPO提供了一个独特的机会,使其成为能够抵御外部噪声注入的稳健模拟存储器。通过上述机制,我们可以在量子有限精度上稳定地存储模拟信息。

1)光延迟线耦合方案
在下图所示的配置中,N个独立的DOPO同时作为N个光脉冲在单个光纤环腔中循环,环腔内部的PSA由泵浦脉冲序列从外部驱动。
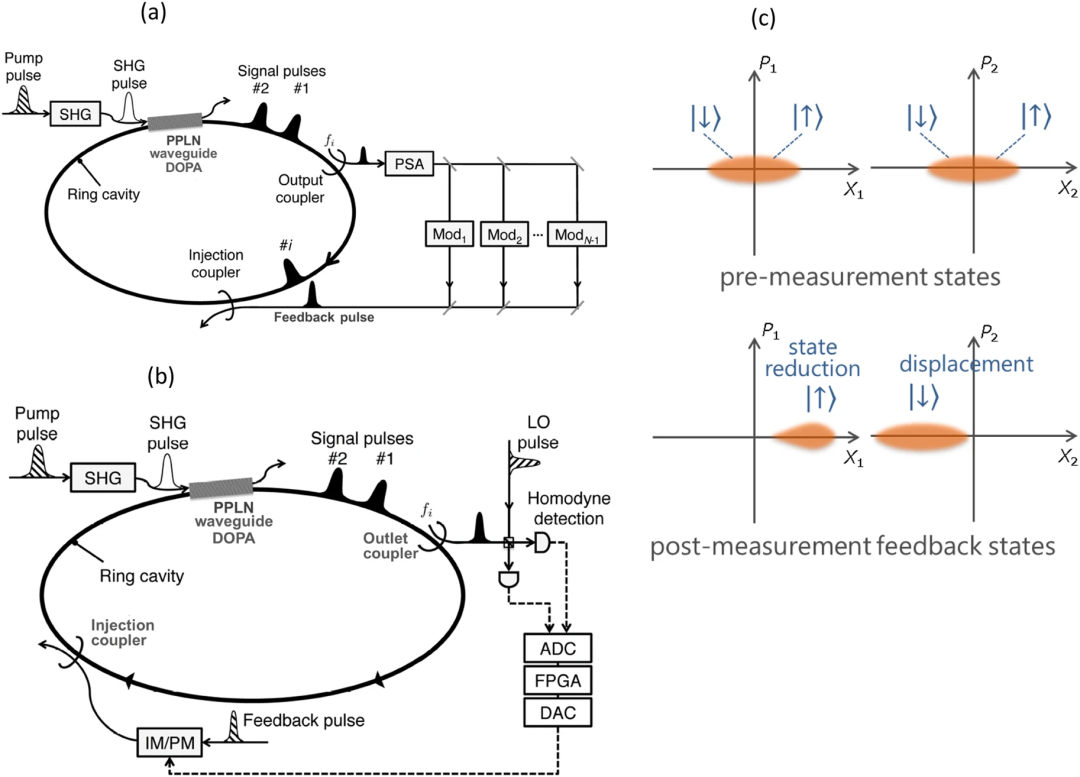
两种相干伊兴机(CIM)。a)相干伊辛机(CIM)基于光延迟线实现相互耦合的时分复用DOPO脉冲。b)带有测量反馈电路的CIM。每个DOPO信号脉冲的一小部分通过输出耦合器外耦,其同相振幅由光学平衡同调探测器测量,其中LO脉冲直接来自脉冲泵浦激光器
上图显示了在DOPO网络中实现伊辛耦合的一种实验方案,即在光纤环谐振器中循环的每个DOPO脉冲的一部分在每次往返时都会被输出耦合器拾取,经外部PSA放大后分割成包括强度和相位调制器在内的多条光延迟线,然后在适当的时间注入目标DOPO脉冲。
2)测量-反馈耦合方案
图(b)显示了实现伊辛耦合Jij的另一种耦合方案。我们可以通过光学平衡零拍探测器(optical balanced homodyne detectors)测量内部DOPO脉冲的近似同相振幅,而不是直接用光延迟线连接DOPO脉冲。如果第j个DOPO脉冲的推断同相振幅用以下公式表示:
![]()
这种测量-反馈耦合方案等同于光延迟线耦合方案,但有以下优缺点。
测量-反馈方案的优点是,可以通过单个测量-反馈电路实现~N^2连接量级的全对全耦合,从而避免了构建N-1条光延迟线并稳定其延迟长度(或光相位)而误差远小于光波长的艰巨任务。
从量子力学的角度来看,光延迟线耦合和测量-反馈耦合方案在工作原理上有微妙但重要的区别。
测量-反馈方案不会在DOPO脉冲之间产生任何纠缠。总密度算子保持在单个DOPO脉冲密度算子的乘积状态,因为耦合是由本地操作和经典通信(LOCC)提供的。然而,测量反馈方案能够实现非单元态还原,从网络中抽走虚假熵,使每个DOPO脉冲接近量子测量引起的海森堡极限(最小不确定性波包)。
在阈值以上,波包实际上是非高斯的,这有助于增强量子并行搜索过程中的量子隧穿。

1)光延迟线耦合CIM
第一个实验性CIM利用自由空间多脉冲DOPO实现了N=4个伊辛自旋,并通过N-1(=3)条光延迟线实现了全对全连接。
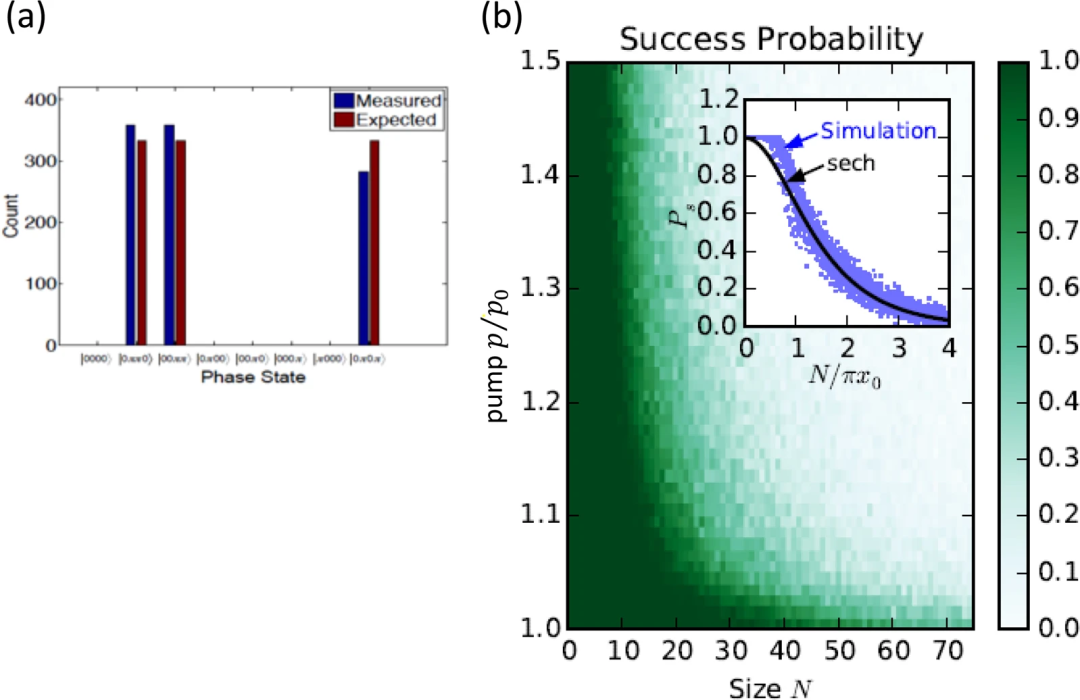
光延迟线耦合CIM的性能。a)针对MAX-CUT-3问题,在N=4 CIM中运行1000次的最终状态直方图。b)对于一维环模型,成功概率是问题大小N和泵浦速率p的函数
如图(a)所示,当泵功率逐渐增大时,机器会以相等的概率找到这个完整图形的三个退化基态之一。另一方面,如果关闭伊辛耦合,机器会通过自发对称破缺随机从8个状态中选择一个。
第二个实验性CIM使用自由空间多脉冲DOPO实现了N=16个伊辛自旋,并分别使用两条或三条光延迟线将它们稀疏地连接起来,以实现一维环形或莫比乌斯梯形图配置。伊辛耦合常数是均匀的。同样,机器找到退化基态之一的概率几乎相等。
这两台CIM找到基态的成功概率为100%,实现了对退化基态的随机取样能力。
2)测量-反馈CIM作为精确解算器
斯坦福大学安装了一套基于测量-反馈的CIM,其中N=100个DOPO脉冲完全由一个测量反馈电路连接。
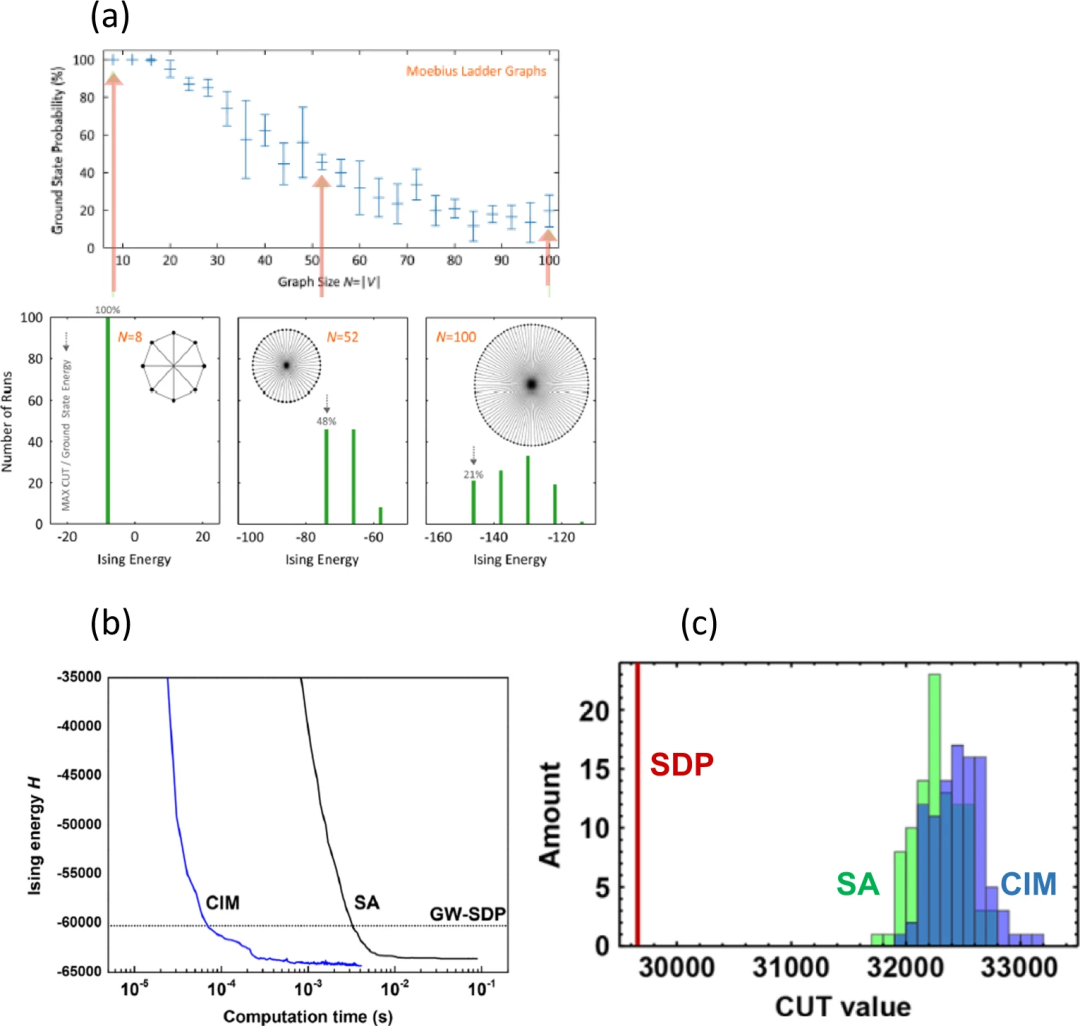
测量-反馈耦合CIM的性能。(a)不同大小的莫比乌斯梯形图的测量-反馈耦合CIM结果。(上图)单次运行中获得莫比乌斯梯形图基态的观测概率与图形大小N的函数关系。对每种图形大小进行了多批100次运行,以获得标准偏差,标准偏差显示为误差条。(下图)插图中所示图形在100次运行中获得的解的直方图(b)在求解完整图形K2000时,使用CIM(蓝色曲线)和SA(黑色曲线)获得的伊辛能量的时间演变。(c)用CIM、SA和GW-SDP解决2000节点图上的MAX-CUT问题时得到的切值
图(a)显示了观测到的莫比乌斯梯形图找到基态的成功概率与图形大小的函数关系,还显示了获得低能激发态和基态的直方图。在N=100的情况下,CIM可以从约10^30个候选解中找到基态,概率为21 ± 9%。在这个实验中,振幅异质性并没有被主动抑制。根据理论预测,当DOPO振幅保持一致时,问题规模达到N=100时的成功概率为~100%。
3)作为近似解算器的测量反馈CIM
与斯坦福CIM相比,主要变化是光纤长度从300米增加到1千米,脉冲重复频率从100兆赫增加到1千兆赫。
图(b)显示了在N=2000个具有全对全连接的完整图中,观察到的伊辛能与MAX-CUT问题的计算时间对比。实验CIM达到这一目标的时间为70μs,而在最先进的中央处理器(CPU)上实现的模拟退火(SA)达到同一目标的时间为2.1ms。
图(c)显示了目前理论精度最高的SDP、目前最流行的启发式SA和CIM的最终能量(或切值)直方图。CIM在精确度方面的表现也优于SA和SDP。在这次精度测量中,SDP、SA和CIM的计算时间分别为100秒、50毫秒和5毫秒。

在中央处理器或超级计算机(PEZY-Shobu)中作为算法实现的四种经典神经网络模型,以及通过Goemans-Williamson半有限编程达到87.8%精度水平所需的计算时间

1)量子极限的光神经网络
光神经网络的独特之处在于其运行模式从量子极限到经典极限的连续交叉。
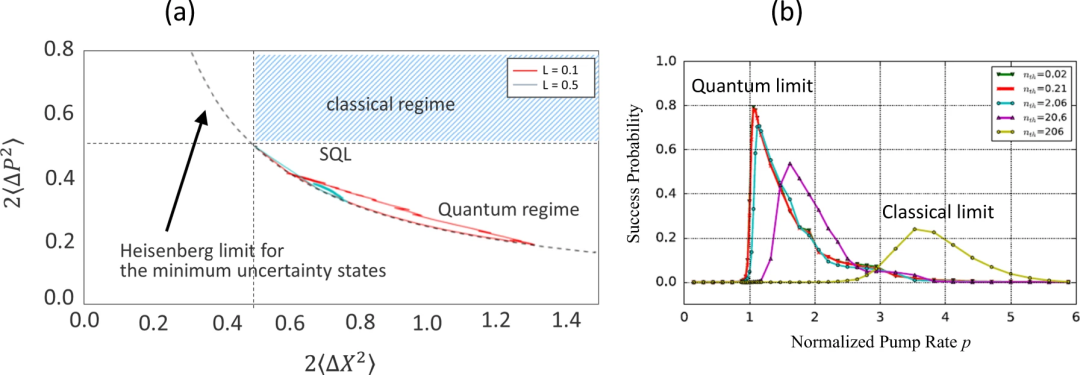
在量子和经典极限下运行的CIM
2)CIM的三步量子计算
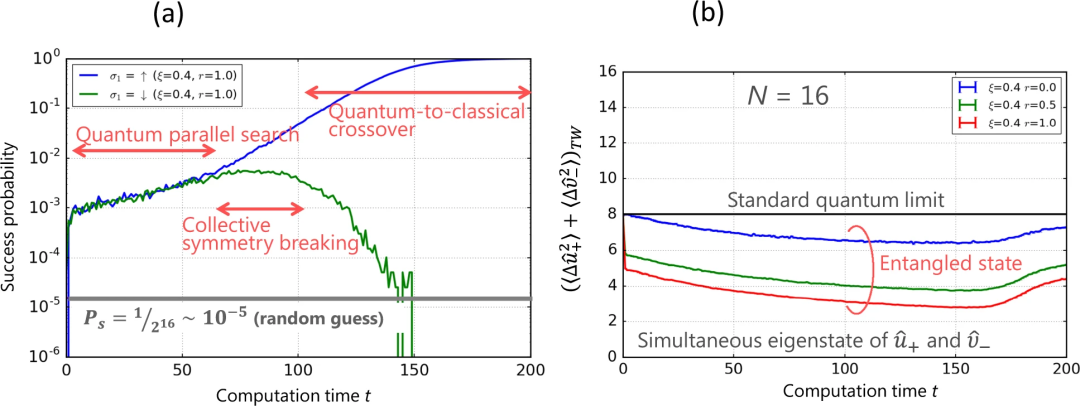
CIM中的三步量子计算和纠缠。a)找到具有反铁磁耦合的N=16 1D伊辛自旋的两个退化基态的成功率与归一化时间t/tc的关系;b)类EPR算子的总方差与归一化时间t/tc的关系
上图展示了光延迟线耦合CIM的三步量子计算。在N=16个具有反铁磁耦合的一维伊辛自旋中,找到两个退化基态中任何一个的成功率是归一化计算时间t/tc的函数,其中tc是往返时间。
经过几次往返后,由于量子噪声相关性的形成,成功率提高了两个数量级,这一趋势一直持续到t/tc=60,此时每个DOPO脉冲的平均光子数达到n=1,集体对称性破缺开始启动。
一个基态被选中,而另一个则未被选中。找到被选中的基态的概率呈指数增长,而找到未被选中的基态的概率呈指数下降。成功率的指数增长得益于玻色终态刺激和相关的交叉增益饱和。阈值以下的量子平行搜索、阈值以上的集体对称性破缺和阈值以上的量子到经典交叉是CIM的三个主要步骤。
3)量子纠缠
在上述由反铁磁耦合伊辛自旋组成的N=16一维环的例子中,基态应该是相邻DOPO的同相振幅Xi和Xi±1负相关。这一观察结果促使我们定义一个类似EPR的算子:
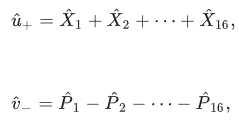
实验表明,在计算时间(或泵浦速率)的很大范围内,光延迟线耦合CIM确实在系统中建立了量子纠缠。
4)量子相干性
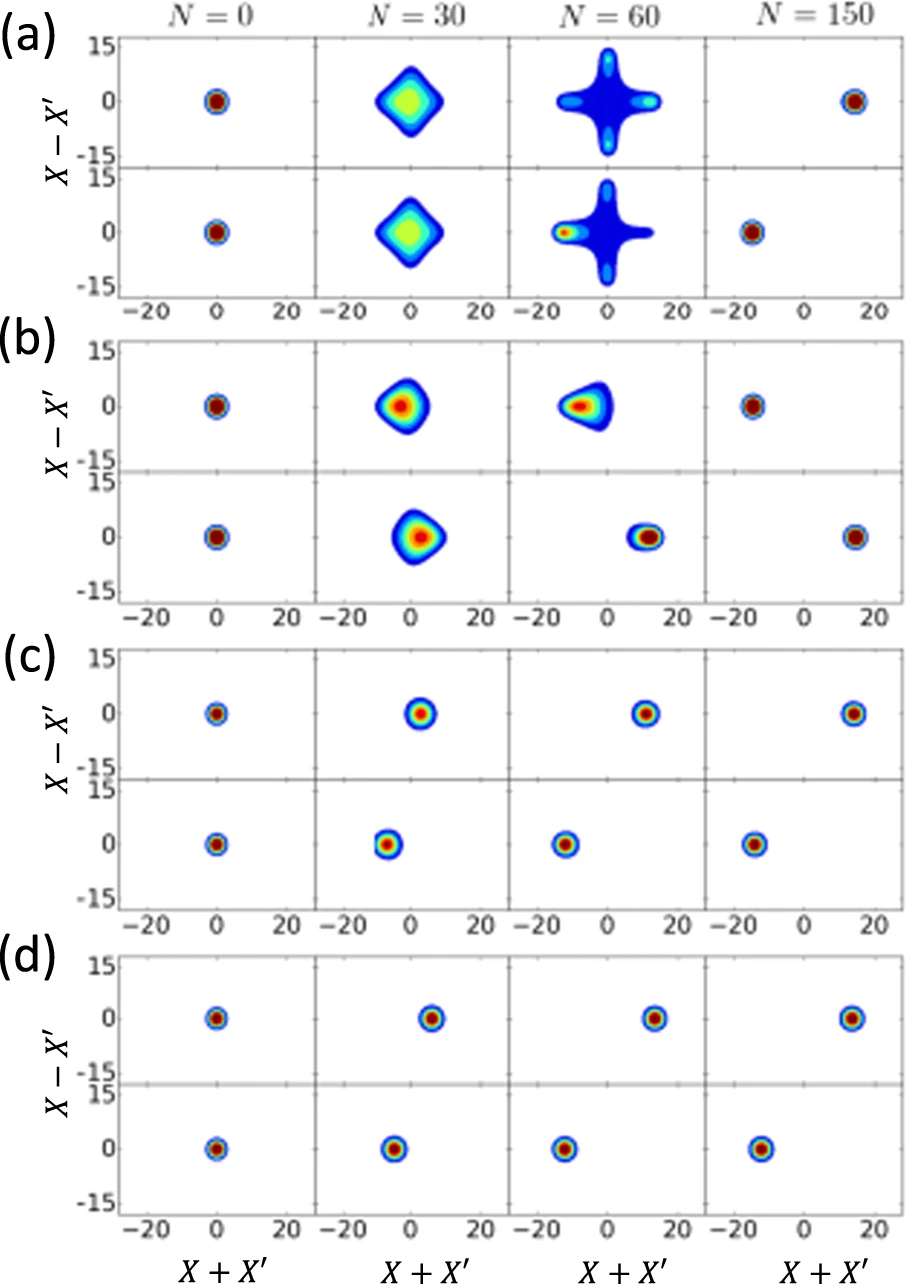
CIM中密度算子的演变
上图显示了密度矩阵元素的等值线图。无论如何,量子相干在CIM中始终存在,无论空腔损耗(cavity loss)有多大。
5)Gottesman -Knill定理
并非所有量子动力学都难以用经典数字计算机模拟。一些有代表性的重要量子过程,包括纠缠态的产生和纯化,都可以用经典方法有效地模拟:因此单靠这样一个量子系统,其计算能力不可能超过当前数字计算技术的水平。
戈特曼(Daniel Gottesman)和克尼尔(Emanuel Knill)是第一个指出经典和量子信息处理之间这一微妙区别的人。
如果一个量子过程从
1)计算基态;
2)使用一组有限的(克利福德群,Clifford group)单元门,如哈达玛门、相位门和受控-非门,并以下列情况结束;
3)沿着计算基态进行投影测量。
这样的量子过程可以用经典数字计算机有效地模拟。熟悉著名的肖尔因式分解算法的读者都知道,它需要实现分数相位,而分数相位并不包含在上述克利福德群约束中,因此肖尔算法不在上述限制范围内。
如果将上述定理与CIM对照,我们可以发现增益饱和(或双光子吸收)和单光子损耗是使CIM难以用经典方法有效模拟的两个基本量子动力学。
事实上,基于精确理论找到N=16一维伊辛自旋问题基态的成功率高于基于高斯近似的成功率。

至此,我们已经解释完CIM的工作原理和理论实验。
光神经网络可以在量子极限(kBT/?ω?1)的室温下运行,并实现基于挤压真空态的量子并行搜索。这种CIM由两个组成器件构成:量子神经元和量子突触。
量子神经元由变性光参量放大器/振荡器提供,在低于振荡阈值时实现量子并行搜索,在阈值时基于集体对称性破缺进行决策,在阈值以上时利用玻色终态刺激实现计算结果的量子到经典放大。量子突触通过与光延迟线的直接耦合或与测量反馈电路的间接耦合实现。它们利用不同的计算资源:光延迟线耦合CIM中的量子噪声相关性(纠缠)和测量反馈CIM中的测量诱导波包还原为非高斯状态。
现在,CIM可以将各种组合优化问题映射到NP-hard的伊辛问题上,从而解决这些问题。量子极限(CIM)下的光神经网络可以利用叠加态进行量子并行搜索求解,从而超越经典机制下的光神经网络。
而在现实情况下,增益饱和和单光子损耗是使CIM难以用经典方法模拟的两个不可或缺的因素。这两个耗散过程和来自外部储层的相关波动是加速搜索过程的关键资源。
自2019年以来,学术机构、政府机构和软件公司开展众多联合CIM研究项目,其中包括:
- 圣母大学研究连续时间模拟计算的极限,以探索提高CIM性能的途径;
- 东京工业大学重点开发CIM在压缩发送和药物发现方面的应用;
- 加州理工学院开发出一种高速微型CIM,由片上100 GHz 脉冲泵浦激光源和片上参量振荡器装置组成;
- 康奈尔大学通过开发错误检测和纠错反馈来探索量子神经网络;
......
由于CIM能够解决传统计算机需要数年才能解决的难题,它可能会在许多应用中大显身手。
对于制药公司来说,通过试验和错误来测试候选药物是一个成本高、效率低的过程。化学物质可以以指数级的数量组合,但只有少数几种组合的化合物能在试验中取得成功。CIM有可能让研究人员更快地测试不同的组合并确定有前景的组合,从而节省资金、资源和时间。
金融应用涉及众多潜在因素和变量,包括投资组合或投资组合池中的固定金额、风险和法律因素、不同利率等。这些众多的因素使得在传统计算机上很难找到最优解,CIM可以将众多因素考虑在内,并产生优化的解决方案。
CIM也可能被证明是机器学习等人工智能应用的有利工具。目前,麻省理工学院正在研究如何应用类似CIM的硬件来加速深度神经网络。
CIM的这些实验性实现利用了光纤时间多路复用技术,该技术可在不同波长上对光学数据进行时间和空间多路复用。这使硬件能够最大限度地利用能源,以极高的效率产生较高的整体计算性能。
与安装在需要超低温和超高真空的超导电路上的超导量子计算机相比,在室温和常压下运行的CIM也具有极大的成本优势,因为它不需要昂贵的稀释制冷机和液氦,也不需要在计算前进行很长时间的预备制冷,这也大大拓展了CIM真正的应用场景。
一些研究人员预测,到2030年代初,CIM将投入商用。
目前来看,预计相干伊辛机(CIM)将会更快的投入落地商业化过程中,相关理论和实验研究将相互促进并同步加速该领域的进步。
参考链接(上下滑动查看更多):
[1]https://www.nature.com/articles/s41534-017-0048-9#Sec18
[2]https://ntt-research.com/in-quest-for-quantum-computing-the-coherent-ising-machine-shows-the-most-promise/
[3]https://physicsworld.com/a/new-ising-machine-computers-are-taken-for-a-spin/
[4]https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr202105fa2.html
[5]https://pubs.aip.org/aip/apl/article/117/16/160501/1061343/Coherent-Ising-machines-Quantum-optics-and-neural
[6]https://mp.weixin.qq.com/s/KrlKTBnCP13gIQmmOpJVjw
[7]https://d-nb.info/1261321219/34
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!