第 120 场 LeetCode 双周赛题解

A 统计移除递增子数组的数目 I

同t3… 当然直接枚举更简单

class Solution {
public:
    long long incremovableSubarrayCount(vector<int> &nums) {
        int n = nums.size();
        int l = 0;//nums[0,r]递增
        while (l + 1 < n && nums[l] < nums[l + 1])
            l++;
        int r = n - 1;//nums[r,n-1]递增
        while (r != 0 && nums[r - 1] < nums[r])
            r--;
        long long res = 0;
        for (int i = max(0, r - 1); i < n; i++) {
            int rv = i != n - 1 ? nums[i + 1] : INT32_MAX;
            int left = 0, right = min(i, l + 1);
            while (left < right) {
                int mid = (left + right + 1) / 2;
                if (mid == 0 || nums[mid - 1] < rv)
                    left = mid;
                else
                    right = mid - 1;
            }
            res += left + 1;
        }
        return res;
    }
};

B 找到最大周长的多边形

先对 $nums$ 排序，然后枚举 $nums[i](i\ge 2)$ 为最大边时是否可以构成多边形

class Solution {
public:
    using ll = long long;

    long long largestPerimeter(vector<int> &nums) {
        ll res = INT64_MIN;
        sort(nums.begin(), nums.end());
        ll s = nums[0] + nums[1];
        for (int i = 2; i < nums.size(); i++) {
            if (s > nums[i])
                res = s + nums[i];
            s += nums[i];
        }
        return res != INT64_MIN ? res : -1;
    }
};

C 统计移除递增子数组的数目 II

二分：枚举移除递增子数组的可能的右端点 $i$ ，通过二分求使得 $nums[left,i]$ 为移除递增子数组的最大 $left$ ，则以 $i$ 为右端点的移除递增子数组的数目为 $left+1$

class Solution {
public:
    long long incremovableSubarrayCount(vector<int> &nums) {
        int n = nums.size();
        int l = 0;//nums[0,r]递增
        while (l + 1 < n && nums[l] < nums[l + 1])
            l++;
        int r = n - 1;//nums[r,n-1]递增
        while (r != 0 && nums[r - 1] < nums[r])
            r--;
        long long res = 0;
        for (int i = max(0, r - 1); i < n; i++) {
            int rv = i != n - 1 ? nums[i + 1] : INT32_MAX;
            int left = 0, right = min(i, l + 1);
            while (left < right) {
                int mid = (left + right + 1) / 2;
                if (mid == 0 || nums[mid - 1] < rv)
                    left = mid;
                else
                    right = mid - 1;
            }
            res += left + 1;
        }
        return res;
    }
};

D 树中每个节点放置的金币数目

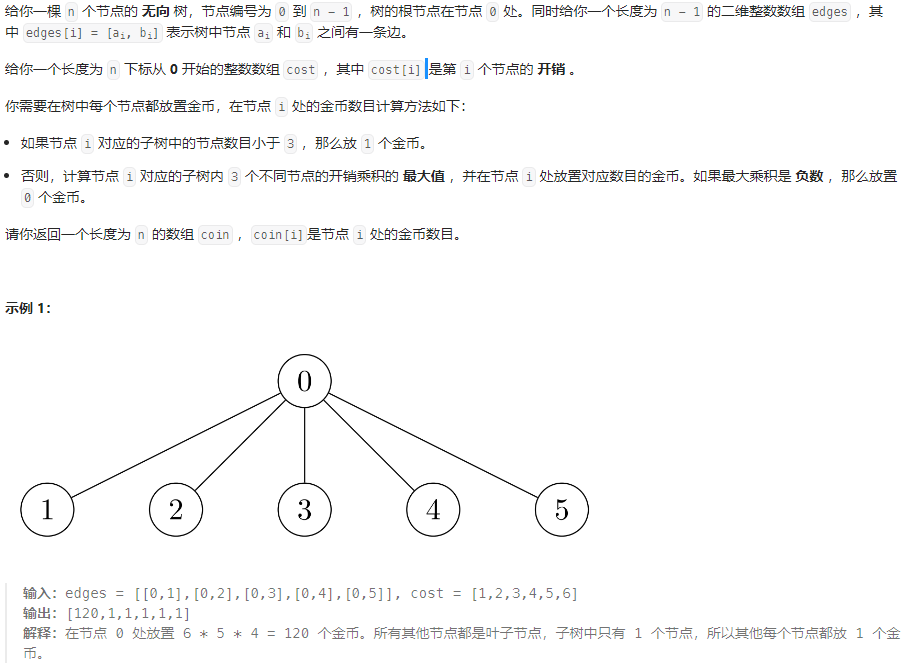
dfs：每个节点保存以当前节点为根的子树中的正数和负数的个数，以及 3 个最大正数和 2 个最小负数（若存在），然后跑 dfs 更新这些信息同时计算答案数组

class Solution {
public:

    struct st {
        vector<int> pos;//升序保存3个正数
        vector<int> neg;//升序保存2个负数
        int cp = 0, cn = 0;//正数和负数的数目

        st() {
            pos = vector<int>(3);
            neg = vector<int>(2);
        }

        void update(int x) {//将x加入当前节点为根的子树
            if (x > 0) {
                if (cp == 0)
                    pos[2] = x;
                else if (cp == 1) {
                    pos[1] = x;
                    if (pos[1] > pos[2])
                        swap(pos[1], pos[2]);
                } else if (cp == 2) {
                    pos[0] = x;
                    if (pos[0] > pos[1])
                        swap(pos[0], pos[1]);
                    if (pos[1] > pos[2])
                        swap(pos[1], pos[2]);
                } else {
                    if (x > pos[0]) {
                        pos[0] = x;
                        sort(pos.begin(), pos.end());
                    } else if (x > pos[1]) {
                        pos[1] = x;
                        sort(pos.begin(), pos.end());
                    } else if (x > pos[2])
                        pos[2] = x;
                }
                cp++;
            } else {
                if (cn == 0)
                    neg[1] = x;
                else if (cn == 1) {
                    neg[0] = x;
                    if (neg[0] > neg[1])
                        swap(neg[0], neg[1]);
                } else {
                    if (x < neg[1]) {
                        neg[1] = x;
                        if (neg[0] > neg[1])
                            swap(neg[0], neg[1]);
                    } else if (x < neg[0])
                        neg[0] = x;
                }
                cn++;
            }
        }

        void update(st &node) {//将node为根的子树加入当前节点为根的子树
            for (auto pi: node.pos)
                if (pi != 0)
                    update(pi);
            for (auto ni: node.neg)
                if (ni != 0)
                    update(ni);
        }

        long long get() {//当前节点的金币数目
            if (cp + cn < 3)
                return 1;
            if (cp == 0)
                return 0;
            long long res = 0;
            if (cp >= 3)
                res = max(res, 1LL * pos[0] * pos[1] * pos[2]);
            if (cn >= 2)
                res = max(res, 1LL * pos[2] * neg[0] * neg[1]);
            return res;
        }
    };


    vector<long long> placedCoins(vector<vector<int>> &edges, vector<int> &cost) {
        int n = cost.size();
        vector<int> e[n];
        for (auto &ei: edges) {//建图
            e[ei[0]].push_back(ei[1]);
            e[ei[1]].push_back(ei[0]);
        }
        vector<st> li(n);
        vector<long long> res(n);
        function<void(int, int)> dfs = [&](int cur, int par) {
            li[cur].update(cost[cur]);
            for (auto j: e[cur])
                if (j != par) {
                    dfs(j, cur);
                    li[cur].update(li[j]);
                }
            res[cur] = li[cur].get();
        };
        dfs(0, -1);
        return res;
    }
};