《数据结构、算法与应用C++语言描述》- 最小赢者树模板的C++实现
赢者树
完整可编译运行代码见:Github::Data-Structures-Algorithms-and-Applications/_30winnerTree
比赛规则
假定有 n 个选手参加一次网球比赛。比赛规则是“突然死亡法”(sudden-death mode):一名选手只要输掉一场球,就被淘汰。一对一对选手比赛,最终只剩下一个选手保持不败。这个“幸存者”就是比赛赢者。
比赛建模
为了便于计算机的实现,将赢者树限制为完全二叉树,这样可以使得比赛的场次最少。每个外部节点表示一名选手,每个内部节点表示一场比赛,该节点的孩子表示比赛的选手。在同一层的内部节点代表一轮比赛,可以同时进行。
定义
赢者树:每一个内部节点所记录的都是比赛的赢者。
输者树:每一个内部节点所记录的都是比赛的输者,晋级的节点记录在边上。
竞赛树也称为选择树(selection tree)。
**定义 13-1[赢者树]**有 n 个选手的一棵赢者树是一棵完全二叉树,它有 n 个外部节点和n-1 个内部节点,每个内部节点记录的是在该节点比赛的赢者。
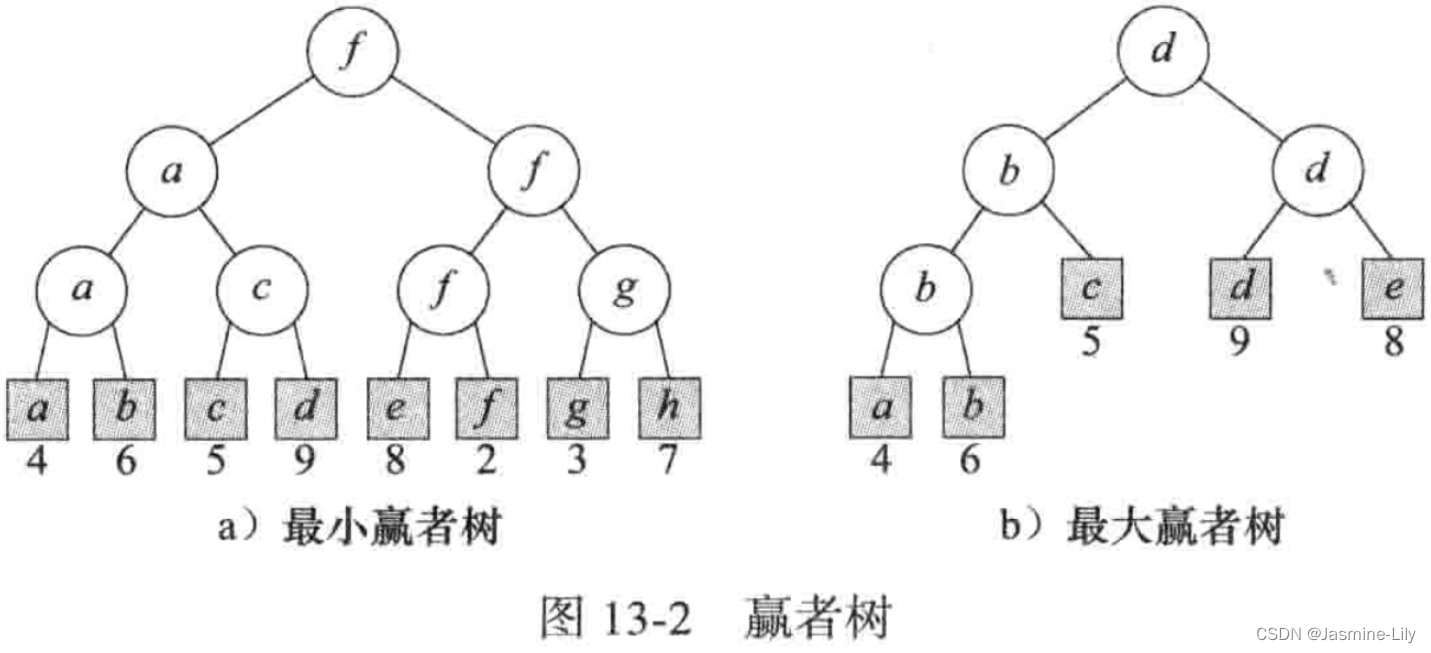
分数&赢者:为了确定一场比赛的赢者树,我们假设每个选手都有一个分数,而且有一个规则用来比较两个选手的分数以确定赢者。在**最小赢者树(min winner tree)中,分数小的选手获胜。在最大赢者树(max winner tree)中,分数大的选手获胜。在分数相等,即平局的时候,左孩子表示的选手获胜。**图 13-2a 是一棵有 8 名选手的最小赢者树,而图 13-2b 是一棵有 5 名选手的最大赢者树。每个外部节点下面的数字表示选手的分数。
赢者树优点
- 当一名选手的分数改变时,修改竞赛树比较容易。例如,当选手 d 的分数由 9 改为1时,只有从 d到根的路径上的节点所表示的比赛可能需要重赛,而其他比赛的结果不受影响。有时,甚至连这种路径上的一些比赛也不需要重赛。例如,在图13-2a 中,当 b 的分数从 6 改为 5 时,在其父节点的比赛中,b 仍为输家,因此 b 的祖父及曾祖父节点所表示的比赛都不必重赛。
在一棵 n 个选手的赢者树中,当一个选手的分数发生变化时,需要修改的比赛场次介于 1 ~ ? l o g 2 n ? 1\sim\lceil log_2n\rceil 1~?log2?n?之间。因此,赢者树的重构需耗时O(logn)。 - n个选手的赢者树可以在0(n)时间内初始化,方法是沿着从叶子到根的方向,在内部节点进行 n-1 场比赛。
与堆相比,赢者树的优点?
在排序时:
堆每次取出最小值之后,把最后一个数放到堆顶,调整堆的时候,每次都要选出父节点的两个孩子节点的最小值,然后再用孩子节点的最小值和父节点进行比较,所以每调整一层需要比较两次。
赢者树每次取出最小值(赢者)之后,就将最小值的选手分数设置为 ∞ \infty ∞,调整赢者树,重新获取赢者;因此,赢者树每次比较只用跟自己的兄弟节点进行比较就好,所以用赢者树树可以比堆少一半的比较次数。
应用
赢者树排序
可以用一棵最小赢者树,用时 Θ ( n l o g n ) \Theta(nlogn) Θ(nlogn)对 n 个元素排序。首先,用n 个元素代表n名选手对赢者树进行初始化。关键字决定每场比赛的结果,总冠军是关键字最小的元素。将该元素的关键字改为最大值(如 ∞ \infty ∞),使它赢不了其他任何选手。然后重构赢者树,以反映出该元素的关键字的变化。这时的总冠军是按序排在第二的元素。将该元素的关键字改为 ∞ \infty ∞。再一次重构赢者树。这时的总冠军是按序排在第三的元素。以此类推,可以完成n个元素的排序。赢者树初始化的用时为0(n)。每次改变赢者的关键字并重构赢者树的用时为0(logn),因为在从一个外部节点到根的路径上,所有的比赛需要重赛。赢者树的重构共需n-1次。整个排序过程的时间为 Θ ( n + n l o g n ) = Θ ( n l o g n ) \Theta(n+nlogn)=\Theta(nlogn) Θ(n+nlogn)=Θ(nlogn)。
归并排序
内部排序与外部排序
内部排序法(internal sorting method):要求待排序的元素全部放入计算机内存。
缺点:当待排序的元素所需要的空间超出内存的容量时,内部排序法就需要频繁地访问外部存储介质(如磁盘),那里存储着部分或全部待排的元素。这使得排序效率大打折扣。插入排序与堆排序等都是内部排序。
**外部排序法(extemal sorting method)**两个步骤:
1)生成一些初始归并段(run),每一个初始归并段都是有序集;
2)将这些初始归并段合并为一个归并段。
举例:假设待排序的记录有 16 000个,使用内部排序一次最多可排序 1000 个记录。在步骤 1)中,重复以下操作 16 次,可得到 16 个初始归并段:
- 输入 1000 个记录
- 用内部排序法对这1000个记录排序
- 输出排序结果,即归并段
- 生成初始归并段之后,我们开始合并归并段,即步骤 2)。在这个步骤中,我们进行若干次归并。每一次归并,都是将最多k个归并段合并成一个归并段,归并段的个数也因此降到归并前的1/k。这个过程持续到归并段的个数等于1为止。
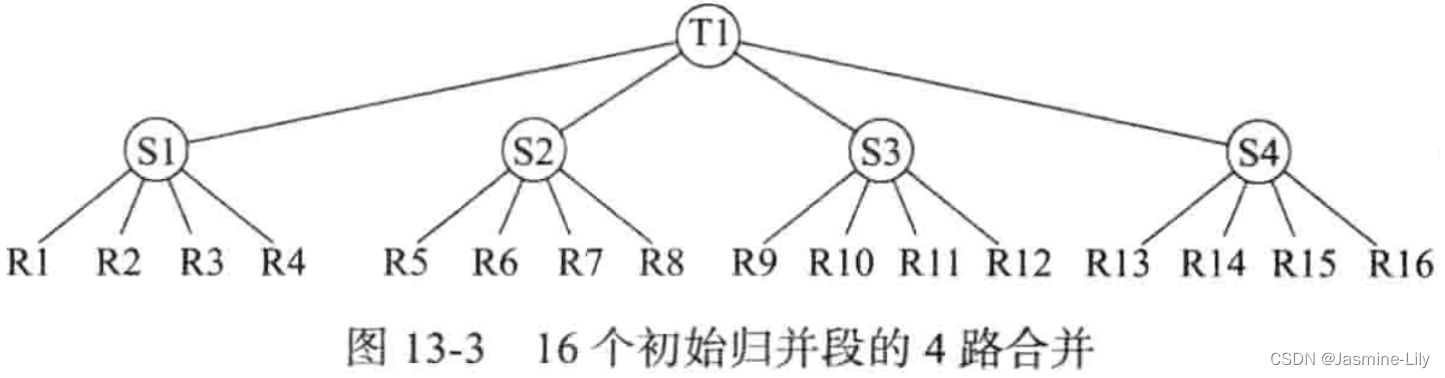
本例有 16 个初始归并段(如图 13-3 所示)。它们的编号分别为 R1,R2,.,R16。在第一次归并过程中,先将 R1~R4 合并为 S1,其长度为 4000 个记录。然后将 R5~R8 合并,以此类推。在第二次归并过程中,将S1~S4合并为T1,它是外部排序的最终结果。
合并k个归并段
简单方法:从k个归并段的前面,不断把关键字最小的元素移到正在生成的输出归并段。当所有元素从 k个输入归并段移至输出归并段时,合并过程就完成了。注意,在选择输出归并段的下一元素时,在内存中只需要知道每个输入归并段的首元素的关键字即可。因此,只要有足够的内存来保存k个关键字,就可以合并k个任意长度的归并段。
实际应用中,要求每一次能输入/输出很多元素,以减少输入/输出的次数。
在上列待排的 16 000 个记录中,每个归并段有 1000 个记录,而内存容量也是 1000 个记录。为了合并前4个归并段,可将内存分为5个缓冲区,每个缓冲区的容量为200个记录。前4个为输入缓冲区,第5个为输出缓冲区。**从前4个输入归并段各取200个记录放入4个输入缓冲区。把合并的记录放入输出缓冲区。**不断把输入缓冲区的记录合并后放入输出缓冲区,直到以下的一个条件满足为止:
1)输出缓冲区已满。
2)某一输入缓冲区变空。
当第一个条件满足时,将输出缓冲区的记录写入磁盘,写完之后继续合并。当第二个条件满足时,从空输入缓冲区对应的归并段继续读取记录到空输入缓冲区,读取过程结束之后,继续合并。当4000个记录都写入一个归并段S1时,前4个归并段的合并过程结束。
时间复杂度:每一个元素合并到输出归并段所需时间为 O(k),因为每一次迭代都需要在k个关键字中找到最小值。因此,产生一个大小为 n 的归并段所需要的总时间为O(kn)。
赢者树k路合并
首先用 Θ ( k ) \Theta(k) Θ(k)的时间初始化一棵有k个选手的赢者树,这k个选手分别是k个归并段的头元素。然后将赢者移入输出归并段,并从相应的输入归并段中取出下一个元素替代赢者的位置。若该输入段无下一个元素,则用一个关键字值很大(不妨为 ∞ \infty ∞)的元素替代。这个提取和替代赢家的过程需要n次,一次需要时间为O(logk)。一次k路合并的总时间为O(k+nlogk)。
赢者树抽象数据类型
假设选手的个数是固定的。也就是说,如果初始化时的选手个数为n,那么初始化之后不能再增减选手。

赢者树的实现
表示
假设用完全二叉树的数组表示来表示赢者树。一棵赢者树有 n名选手,需要 n-1 个内部节点tree[1:n-1]。选手(或外部节点)用数组player[1:n]表示,因此 tree[i]是数组 player的一个索引,类型为int。在赢者树的节点i对应比赛中,tree[i]代表赢者。图13-4给出了在有5选手的赢者树中,各节点与数组 tree 和 player之间的对应关系。
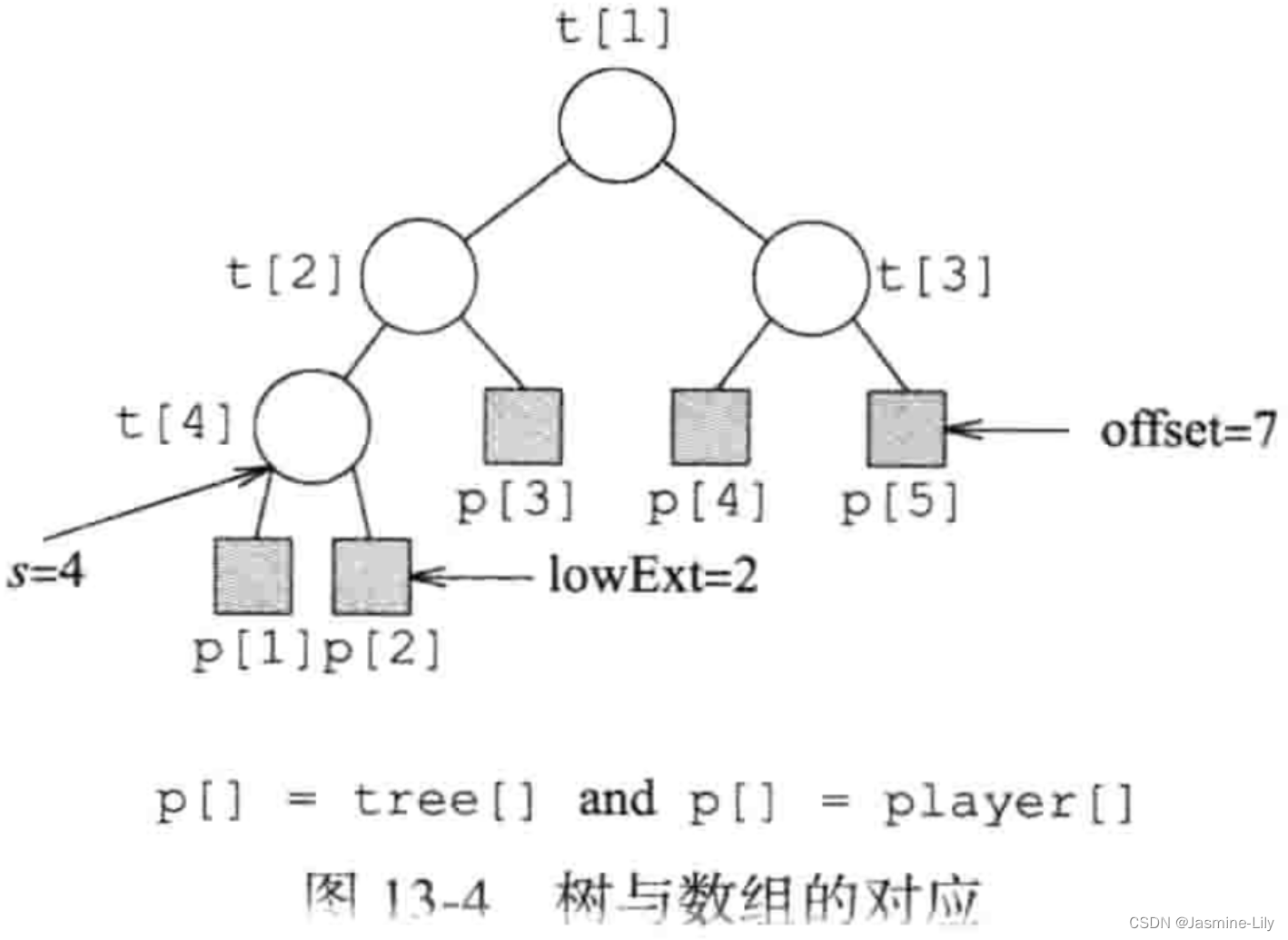
为实现这种对应关系,我们必须能够确定外部节点player[1]的父节点tree[p]。当外部节点的个数为n时,内部节点的个数为n-1。最底层最左端的内部节点,其编号为s,且
s
=
2
?
l
o
g
2
(
n
?
1
)
?
s=2^{\lfloor log_2(n-1)\rfloor}
s=2?log2?(n?1)?。因此,最底层内部节点的个数是 n-s,最底层外部节点个数 lowExt是这个数的 2 倍。例如,在图 13-4 中,n=5,s=4,最底层最左端的内部节点是 tree[4],这一层的内部节点个数是 n-4=1 个。最底层外部节点个数 lowExt=2,倒数第2 层最左端的外部节点号为lowExt+1。令offset =2*s-1。对于任何一个外部节点 player[1],其父节点 tree[p]由以下公式给出:
p
=
{
(
i
+
o
f
f
s
e
t
)
2
i
≤
l
o
w
E
x
t
i
?
l
o
w
E
x
t
+
n
?
1
2
i
>
l
o
w
E
x
t
p=\left\{ \begin{array}{ll} \frac{(i+offset)}{2}&i\leq lowExt\\ \frac{i-lowExt+n-1}{2}&i>lowExt \end{array} \right.
p={2(i+offset)?2i?lowExt+n?1??i≤lowExti>lowExt?
赢者树的初始化
为了初始化一棵赢者树,我们从右孩子选手开始,进行他所参加的比赛,而且逐层往上,只要是从右孩子上升到比赛节点,就可以进行在该节点的比赛。为此,要从左往右地考察右孩子选手。在图13-4的树中,我们首先进行选手player[2]参加的比赛,然后进行选手player[3]参加的比赛,最后进行选手player[5]参加的比赛。首先,我们进行选手player[2]参加的在节点tree[4]的比赛。然后我们进行选手player[3]参加的在节点tree[2]的比赛。最后我们进行选手player[5]参加的在节点tree[3]的比赛和在节点tree[1]的比赛。注意,当在节点tree[i]进行比赛时,参加该比赛的选手已经确定,而且选手的记录已经存储在节点tree[i]的子节点中。
时间复杂度是O(n)。
重新组织比赛
当选手thePlayer的值改变时,在从外部节点player[thePlayer]到根tree[1]的路径上,一部分或全部比赛都需要重赛。为简单起见,我们将该路径上的全部比赛进行重赛。
时间复杂度是log(n)
代码
实现最小赢者树
main.cpp
/*
Project name : _30winnerTree
Last modified Date: 2023年12月19日11点18分
Last Version: V1.0
Descriptions: 最小赢者树——main函数
*/
#include "completeWinnerTree.h"
int main() {
completeWinnerTreeTest();
return 0;
}
completeWinnerTree.h
/*
Project name : _30winnerTree
Last modified Date: 2023年12月19日11点18分
Last Version: V1.0
Descriptions: 最小赢者树——模板类
*/
#ifndef _30WINNERTREE_COMPLETEWINNERTREE_H
#define _30WINNERTREE_COMPLETEWINNERTREE_H
#include <iostream>
#include "winnerTree.h"
#include "myExceptions.h"
void completeWinnerTreeTest();
template<class T>
class completeWinnerTree : public winnerTree<T>
{
public:
completeWinnerTree(T *thePlayer, int theNumberOfPlayers)
{
tree = nullptr;
initialize(thePlayer, theNumberOfPlayers);
}
~completeWinnerTree() {delete [] tree;}
void initialize(T*, int);
[[nodiscard]] int winner() const
{return tree[1];}
[[nodiscard]] int winner(int i) const
// 返回节点i的胜者的index
{return (i < numberOfPlayers) ? tree[i] : 0;}
void rePlay(int);
void output() const;
private:
int lowExt{}; // lowest-level external nodes
int offset{}; // 2^log(n-1) - 1
int *tree; // array for winner tree
int numberOfPlayers{};
T *player; // array of players
void play(int, int, int);
};
template<class T>
void completeWinnerTree<T>::initialize(T *thePlayer,
int theNumberOfPlayers)
{// 使用thePlayer[1:numberOfPlayers]数组初始化赢者树
int n = theNumberOfPlayers;
if (n < 2)
throw illegalParameterValue("must have at least 2 players");
player = thePlayer;
numberOfPlayers = n;
delete [] tree;// 清空tree
tree = new int [n];// 重新为tree初始化空间
// 计算 s = 2^log (n-1)
int i, s;
for (s = 1; 2 * s <= n - 1; s += s);
lowExt = 2 * (n - s);
offset = 2 * s - 1;
// 从最底层的外部节点开始比赛
for (i = 2; i <= lowExt; i += 2)
play((offset + i) / 2, i - 1, i);
// 处理剩余的外部节点
if (n % 2 == 1) // 当n是奇数时,总是有一场内部节点和外部节点的比赛
{
play(n/2, tree[n - 1], lowExt + 1);
i = lowExt + 3;
}
else i = lowExt + 2;
// i是最右边的外部节点
for (; i <= n; i += 2)
play((i - lowExt + n - 1) / 2, i - 1, i);
}
template<class T>
void completeWinnerTree<T>::play(int p, int leftChild, int rightChild)
{// 开展tree[p]处的比赛
// leftChild是p的左孩子
// rightChild是p的右孩子
// 定义的是数越小就胜出
tree[p] = (player[leftChild] <= player[rightChild]) ?
leftChild : rightChild;
// 如果p是右孩子
while (p % 2 == 1 && p > 1)
{// 从右孩子开始
tree[p / 2] = (player[tree[p - 1]] <= player[tree[p]]) ?
tree[p - 1] : tree[p];
p /= 2; // 到其父亲节点
}
}
template<class T>
void completeWinnerTree<T>::rePlay(int thePlayer)
{// 为玩家thePlayer重新组织比赛
int n = numberOfPlayers;
if (thePlayer <= 0 || thePlayer > n)
throw illegalParameterValue("Player index is illegal");
int matchNode, // 进行下一场比赛的节点
leftChild, // matchNode的左孩子
rightChild; // matchNode的右孩子
// 找到第一个match节点和他的孩子
if (thePlayer <= lowExt)
{// 从最底层开始
matchNode = (offset + thePlayer) / 2;
leftChild = 2 * matchNode - offset;
rightChild = leftChild + 1;
}
else
{
matchNode = (thePlayer - lowExt + n - 1) / 2;
if (2 * matchNode == n - 1)
{
leftChild = tree[2 * matchNode];
rightChild = thePlayer;
}
else
{
leftChild = 2 * matchNode - n + 1 + lowExt;
rightChild = leftChild + 1;
}
}
tree[matchNode] = (player[leftChild] <= player[rightChild])
? leftChild : rightChild;
// 第二场比赛的特殊情况
if (matchNode == n - 1 && n % 2 == 1)
{
matchNode /= 2; // move to parent
tree[matchNode] = (player[tree[n - 1]] <=
player[lowExt + 1]) ?
tree[n - 1] : lowExt + 1;
}
// 进行其他比赛,也就是父亲节点的比赛
matchNode /= 2; // 移动到父亲节点
for (; matchNode >= 1; matchNode /= 2)
tree[matchNode] = (player[tree[2 * matchNode]] <=
player[tree[2 * matchNode + 1]]) ?
tree[2 * matchNode] : tree[2 * matchNode + 1];
}
template<class T>
void completeWinnerTree<T>::output() const
{
cout << "number of players = " << numberOfPlayers
<< " lowExt = " << lowExt
<< " offset = " << offset << endl;
cout << "complete winner tree pointers are" << endl;
for (int i = 1; i < numberOfPlayers; i++)
cout << tree[i] << ' ';
cout << endl;
}
#endif //_30WINNERTREE_COMPLETEWINNERTREE_H
completeWinnerTree.cpp
/*
Project name : _30winnerTree
Last modified Date: 2023年12月19日11点18分
Last Version: V1.0
Descriptions: 最小赢者树——测试函数
*/
#include <iostream>
#include "completeWinnerTree.h"
#include "player.h"
using namespace std;
void completeWinnerTreeTest()
{
int n;
cout << "Enter number of players, >= 2" << endl;
cin >> n;
if (n < 2)
{cout << "Bad input" << endl;
exit(1);}
player *thePlayer = new player[n + 1];
cout << "Enter player values" << endl;
for (int i = 1; i <= n; i++)
{
cin >> thePlayer[i].key;
thePlayer[i].id = i;
}
completeWinnerTree<player> *w =
new completeWinnerTree<player>(thePlayer, n);
cout << "The winner tree is" << endl;
w->output();
thePlayer[2].key = 0;
w->rePlay(2);
cout << "Changed player 2 to zero, new tree is" << endl;
w->output();
thePlayer[3].key = -1;
w->rePlay(3);
cout << "Changed player 3 to -1, new tree is" << endl;
w->output();
thePlayer[7].key = 2;
w->rePlay(7);
cout << "Changed player 7 to 2, new tree is" << endl;
w->output();
delete [] thePlayer;
delete w;
}
player.h
/*
Project name : _30winnerTree
Last modified Date: 2023年12月19日11点18分
Last Version: V1.0
Descriptions: id&键值
*/
#ifndef _30WINNERTREE_PLAYER_H
#define _30WINNERTREE_PLAYER_H
struct player
{
int id, key;
operator int () const {return key;}
};
#endif //_30WINNERTREE_PLAYER_H
winnerTree.h
/*
Project name : _30winnerTree
Last modified Date: 2023年12月18日16点28分
Last Version: V1.0
Descriptions: 最小赢者树的抽象类
*/
#ifndef _30WINNERTREE_WINNERTREE_H
#define _30WINNERTREE_WINNERTREE_H
using namespace std;
template<class T>
class winnerTree
{
public:
virtual ~winnerTree() {}
virtual void initialize(T *thePlayer, int theNumberOfPlayers) = 0;
// 使用thePlayer[1:numberOfPlayers]创建赢者树
virtual int winner() const = 0;
// 返回赢者树的index
virtual void rePlay(int thePLayer) = 0;
// 改变选手thePLayer的值之后重新组织比赛
};
#endif //_30WINNERTREE_WINNERTREE_H
myExceptions.h
/*
Project name : _30winnerTree
Last modified Date: 2023年12月18日16点28分
Last Version: V1.0
Descriptions: 异常汇总
*/
#pragma once
#ifndef _MYEXCEPTIONS_H_
#define _MYEXCEPTIONS_H_
#include <string>
#include<iostream>
#include <utility>
using namespace std;
// illegal parameter value
class illegalParameterValue : public std::exception
{
public:
explicit illegalParameterValue(string theMessage = "Illegal parameter value")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// illegal input data
class illegalInputData : public std::exception
{
public:
explicit illegalInputData(string theMessage = "Illegal data input")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// illegal index
class illegalIndex : public std::exception
{
public:
explicit illegalIndex(string theMessage = "Illegal index")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// matrix index out of bounds
class matrixIndexOutOfBounds : public std::exception
{
public:
explicit matrixIndexOutOfBounds
(string theMessage = "Matrix index out of bounds")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// matrix size mismatch
class matrixSizeMismatch : public std::exception
{
public:
explicit matrixSizeMismatch(string theMessage =
"The size of the two matrics doesn't match")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// stack is empty
class stackEmpty : public std::exception
{
public:
explicit stackEmpty(string theMessage =
"Invalid operation on empty stack")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// queue is empty
class queueEmpty : public std::exception
{
public:
explicit queueEmpty(string theMessage =
"Invalid operation on empty queue")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// hash table is full
class hashTableFull : public std::exception
{
public:
explicit hashTableFull(string theMessage =
"The hash table is full")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// edge weight undefined
class undefinedEdgeWeight : public std::exception
{
public:
explicit undefinedEdgeWeight(string theMessage =
"No edge weights defined")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
// method undefined
class undefinedMethod : public std::exception
{
public:
explicit undefinedMethod(string theMessage =
"This method is undefined")
{message = std::move(theMessage);}
void outputMessage() {cout << message << endl;}
private:
string message;
};
#endif
运行结果
"C:\Users\15495\Documents\Jasmine\prj\_Algorithm\Data Structures, Algorithms and Applications in C++\_30winnerTree\cmake-build-debug\_30winnerTree.exe"
Enter number of players, >= 2
8
Enter player values
4
6
5
9
8
2
3
7
The winner tree is
number of players = 8 lowExt = 8 offset = 7
complete winner tree pointers are
6 1 6 1 3 6 7
Changed player 2 to zero, new tree is
number of players = 8 lowExt = 8 offset = 7
complete winner tree pointers are
2 2 6 2 3 6 7
Changed player 3 to -1, new tree is
number of players = 8 lowExt = 8 offset = 7
complete winner tree pointers are
3 3 6 2 3 6 7
Changed player 7 to 2, new tree is
number of players = 8 lowExt = 8 offset = 7
complete winner tree pointers are
3 3 6 2 3 6 7
Process finished with exit code 0
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!