SwinTransformer

patch embedding

????????(b,3,224,224)->(b,N,96) N:patch数量

????????为每个stage中的每个Swin Transformer block设置drop_rate，根据设置[2,2,6,2]，每个Swin Transformer block的drop_path为0~0.1等间距采样的12个小数，参数0.1也可以更改。还有个drop参数设为了0.，注意二者的用处。drop是MLP层以及注意力层的drop概率，drop_path是用于一个drop层的；还有个attn_drop是用于注意力层的。

参数分解

? ? ? ? 已知embed_dim是96，stage1维持embed_dim=96，从stage1到stage4的dim分别是[96,192,384,768]，原图尺寸是224，经过patch embedding长宽各下降4倍，[56,56,96]这是二维表示法，还有[56*56,96]这种token表示法，很多时候，我们操作的张量都是同一个，只不过进行的处理不同，经过的网络层类型（比如卷积和全连接层对输入数据形式的要求就不同）不同，对数据的形式要求不同，但是数据还是同一份数据。贯穿stage1到stage4数据分别是（56,56,96)、(28,28,192)、(14,14,384)、(7,7,768)，这些数据的变化由PatchMerging层引起，包括尺寸的*2下采样和通道数的*2增加；对于每一个stage中的所有Swin Transformer block中的MSA都用相同头数，4个stage分别是[3,6,12,24]，window_size和mlp_ratio分别恒定设为7和4.，恒定的意思是不会随着stage而改变，总共有3个PatchMerging层嵌入在stage和stage之间，stage中的操作是不会改变数据的尺寸的。

Swin Transformer block

????????对输入feature map的分辨率和window_size做了比较，如果分辨率<window_size，那么就设置shift_size=0并且window_size分辨率的最小值（比如window_size=7，如果分辨率是[5，6]那么window_size就会被强制为5）;shift_size必须小于window_size，最小值为0；Swin Transformer block包含这些层：Layer Norm层、注意力层、droppath层、Layer Norm层、MLP层，共5层。

注意力层

????????head_dim是根据每个stage设置的dim和头数决定的，比如stage1,dim=96,heads=3,那么head_dim=96//3=32，这里是整除；scale就是注意力计算公式的分母部分：根号d；

relative_position_bias_table相对位置偏置表

? ? ? ? 初始化为符合截断分布的数据，形状为（（2*window_sizeh-1)*(2*window_sizew-1),num_heads)，比如我的window_size=7，那么相对位置偏置表的形状为(169，3)，以stage1三头注意力为例；torch.meshgrid([coords_h, coords_w])是将第一个序列数据coords_h中的每个元素横向重复，比如coords_h=[1,2]，则结果为[1 1

? ? ? ? ? ? ? ? ? ? ? ? ? 2 2]，将coords_w每个元素纵向重复，结果为[1 2

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???????????1 2]；torch.stack默认dim=0，并且是增加维度的stack操作；torch.flattern(input,start_dim,end_dim)，比如我有张量（1，2，3，4，5，6），执行torch.flatten(x,start_dim=2,end_dim=3)，结果为[1, 2, 12, 5, 6]，也就是start_dim和end_dim都包含，并且相乘的维度就是flatten的维度，其余保持不变，这个可以改变形状，也可以改变维度，但张量还是哪个张量；我们知道每个stage为了保持dim不变，q/k/v的dim都应该和该层的stage保持一致，所以用一个线性层将dim扩大3倍，得到3*dim长度的token，其中每个dim分别代表q/k/v；比如我的输入是（56，56，96）经过这个线性层后变为了（56，56，288），q=k=v=(56，56，96）,由于是三头注意力，将dim按照头数再划分，再经过reshape、permute操作q=k=v=(b,3，56*56，32）（注意这个维度顺序的表示非常重要，因为矩阵乘法和维度的关系很大），q和k的转置相乘得到attn=（b ,?3?, 56*56 , 56*56），attn做个放缩再和v相乘，得到（b ,?3?, 56*56 , 32）。

单头注意力和多头注意力分析

假如是单头注意力，那么q=k=v=(b,56*56,96)，其实四维还是三维不影响矩阵乘法啊，因为矩阵乘法只考虑了最后两维，前面的保持不变。attn=（b ,?56*56 , 56*56），最终得到（b,56*56 , 96），注意两个attn的区分，多头的有多套权重，而单头的只有一套，这有什么影响呢？就是一套权重可能是不准确的，我用多套权重，同时为了保持最后的dim和原始的dim一致，每套权重只作用于部分dim，这里就是dim // num_heads了。总而言之，头数影响的只是权重表的个数。

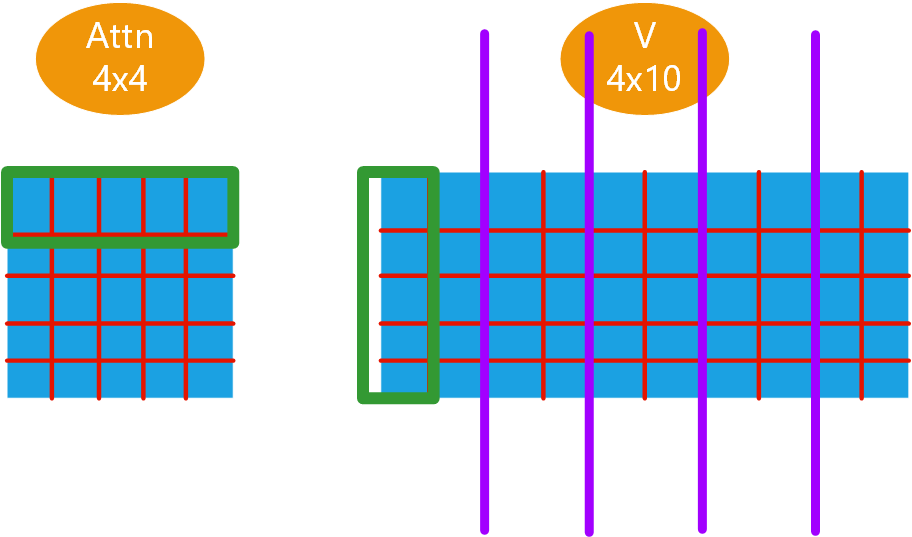
我们来看看引入到注意力里面的相对位置偏置是怎么做的

1.初始化相对位置偏置表

形状为（(2*window_sizeh-1)*(2*window_sizew-1),num_heads)

2.生成相对位置索引

形状为（window_sizeh*window_sizew，window_sizeh*window_sizew），值在0~13*13-1之间，纵向找不出规律，横向就是从第一个数开始以1递减?

3.生成相对位置偏置

形状为（num_heads,window_sizeh*window_sizew，window_sizeh*window_sizew)

反正最终的（49，49）个相对位置编码是从截断分布中取出的，会有重复

? ? ? ? ? ?

????????

? ? ??